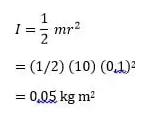Momen inersia sangat penting ketika hendak mempelajari perilaku gerak benda yang ada di muka bumi.
Sebagai contoh pada saat memutar suatu kelereng, pada awalnya kita hanya akan melihat kelereng berputar sangat cepat namun lama – kelamaan akan berhenti bergerak dan kemudian diam.
Contoh di atas dikarenakan oleh adanya momen inersia kelereng yang cenderung untuk diam / mempertahankan pada posisi awal.
Sebetulnya adalah banyak contoh lain dari inersia benda dalam kehidupan sehari – hari, agar lebih jelasnya simak penjelasannya di bawah ini.
Daftar Isi
Pengertian Momen Inersia
Momen inersia atau juga disebut dengan kelembaman suatu benda merupakan suatu kecenderungan sebuah benda dalam mempertahankan kondisinya baik tetap diam maupun tetap bergerak.
Perlu kalian ketahui, jika Hukum kelembaman / hukum inersia merupakan istilah yang sama dengan hukum pertama Newton.
Hukum satu ini dirumuskan oleh Issac Newton yang sudah kalian pelajari waktu duduk dibangku SMP.
Hukum pertama Newton ini memiliki bunyi jika benda yang tak diberi gaya eksternal (gaya dari luar) akan cenderung untuk mempertahankan kondisinya.
Suatu benda yang mencoba dalam mempertahankan kondisinya yang sangat bergantung dengan momen inersia.
Semakin besar inersia, maka benda akan sulit bergerak begitu juga sebaliknya.
Besarnya dari momen inersia sebuah benda bergantung pada beberapa faktor di bawah ini:
- Geometri benda (bentuk).
- Jarak ke sumbu putar benda (lengan momen).
- Letak sumbu putar benda.
- Massa benda atau partikel.
Rumus Momen Inersia
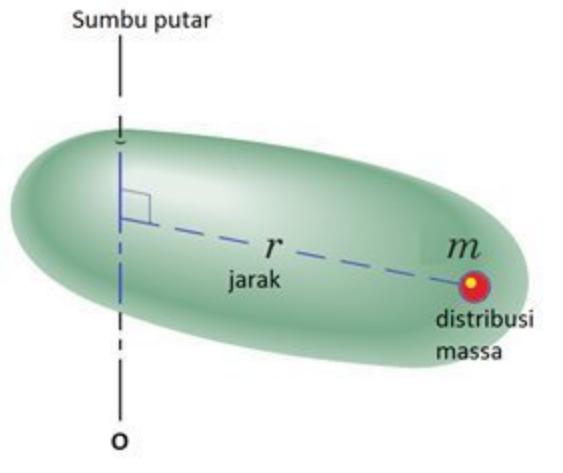
Benda dengan massa m yang mempunyai titik putar dengan jarak r, rumus momen inersianya akan dinyatakan seperti berikut:
I = mr2
Keterangan:
- m = massa benda (kg)
- r = jarak benda pada sumbu putar (m)
Satuan momen inersia bisa diturunkan dari besaran penyusunnya sehingga inersia memiliki satuan Internasional (SI) berupa kg m².
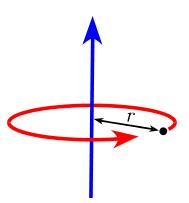
Tak hanya digunakan untuk menyelesaikan momen inersia dari sistem partikel tunggal seperti penjelasan sebelumnya.
Momen inersia ini juga menerangkan pada sistem partikel dengan jumlah yang banyak dimana jumlah dari momen inersia masing – masing komponen pada sistem partikel.
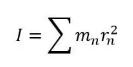
Secara matematis, jika dijabarkan maka akan menjadi seperti berikut ini:
![]()
Notasi Σ (dibaca: sigma) merupakan penjumlahan momen inersia dari sistem partikel sebanyak n.
Momen inersia tak hanya bergantung dengan massa serta jarak pada titik putarnya. Tetapi juga sangat bergantung dengan bentuk benda seperti bentuk batang silinder, bola pejal cincin dan lainnya.
Untuk berbagai benda dengan bentuk yang teratur sudah diketahui secara umum rumus inersianya seperti:
| Benda | Sumbu Putar | Gambar benda | Rumus Momen Inersia |
|---|---|---|---|
| Partikel | Di sebelah partikel dengan jarak R |  | I = mR2 |
| Batang silinder | Tepat melalui pusat dan tegak lurus batang | 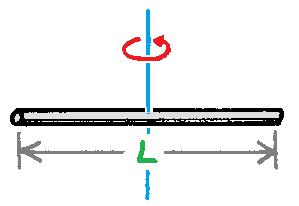 | I = 1/12mL2 |
| Batang silinder | Melalui ujung batang dan tegak lurus batang | 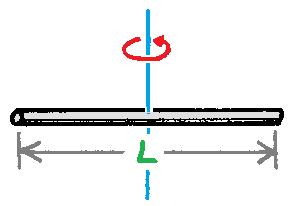 | I = 1/3mL2 |
| Silinder pejal | Melalui titik pusat silinder | 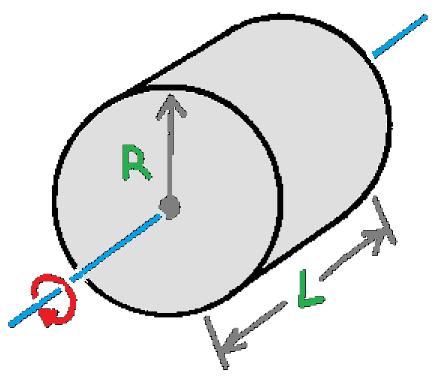 | I = 1/2mR2 |
| Silinder berongga | Melalui titik pusat silinder | 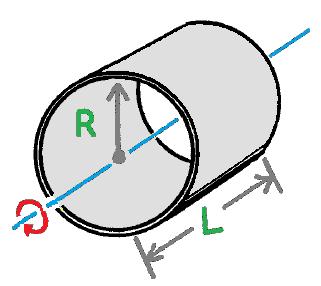 | I = mR2 |
| Silinder pejal berongga | Melalui titik pusat silinder | 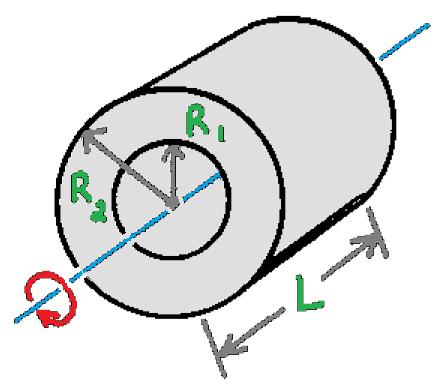 | |
| Silinder pejal | Melintang terhadap titik pusat silinder | 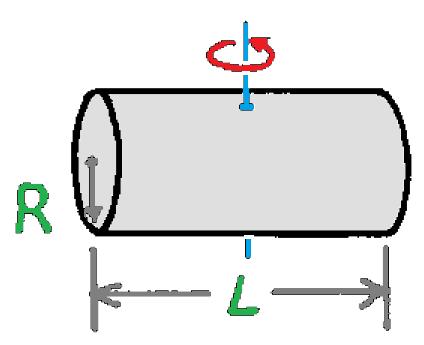 | I = 1/4mR2 + 1/12mL2 |
| Bola pejal | Tepat melalui titik pusat | 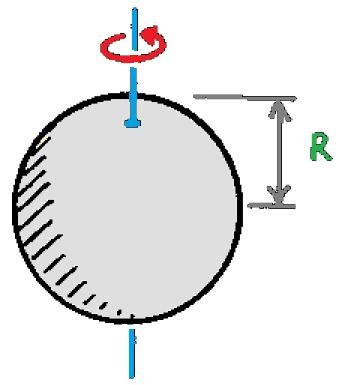 | I = 2/5mR2 |
| Bola berongga | Tepat melalui titik pusat | 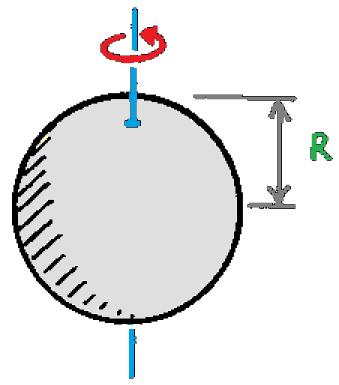 | I = 2/3mR2 |
| Cincin tipis | Melintang terhadap titik pusat cincin | 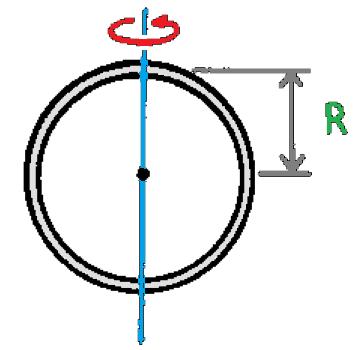 | I = 1/2mR2 |
| Plat datar | Tepat melalui titik pusat plat | 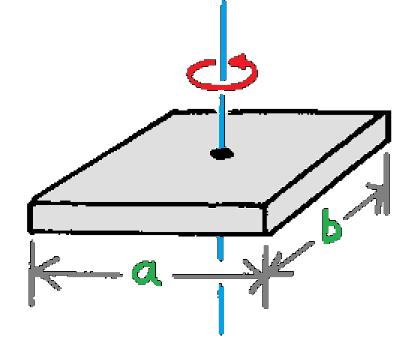 | I = 1/12m (a2 + b2) |
| Kerucut pejal | Melalui titik pusat silinder | 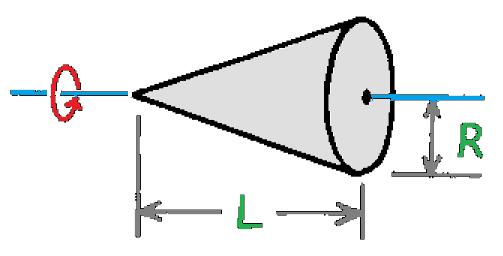 | I = 3/10mR2 |
Contoh Soal
Agar kalian lebih mudah untuk memahami uraian di atas, berikut kami sajikan beberapa contoh soal momen inersia beserta penjelasannya secara lengkap, yaitu:
1. Diberikan suatu batang tipis dengan panjang 4 meter serta massanya adalah 0,2 kg seperti gambar di bawah ini:
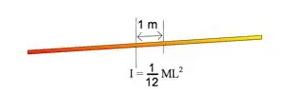
Apabila momen inersia pada poros di pusat massa batang yaitu I= 1/12 ML2 hitung besar inersia batang apabila poros digeser ke arah kanan sejauh 1 meter!
Jawab:
Inersia pada batang pejal, sumbu putar digeser sebesar r=1 m dari arah pusat:
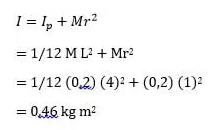
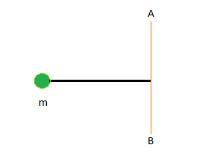
2. Bola dengan massa 100 gram dikarian dengan seutas tali dengan panjang 20 cm seperti gambar di bawah.
Momen Inersia bola pada sumbu AB yaitu?
Jawab:
Inersia suatu bola dengan massa m = 0,1 kg dengan panjang tali r= 0,2 m yaitu:
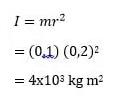
3. Perhatikan gambar di bawah ini!
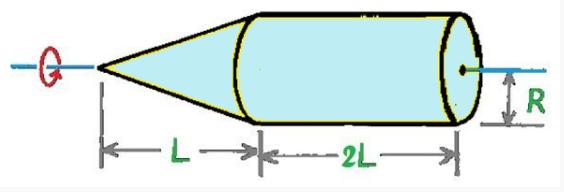
Suatu benda pejal dengan bentuk menyerupai kerucut yang menempel di salah satu ujung silinder diputar dengan sumbu rotasi terhadap titik pusat silinder seperti pada gambar di atas.
Diketahui massa silinder sama seperti massa kerucut yaitu sebesar 2 kg, dengan panjang silinder 0,8 meter, serta jari – jari silinder 0,1 meter.
Hitunglah inersia dari benda tersebut!
Jawab:
Dalam menyederhanakan perhitungannya, maka inersia pada setiap geometri benda dihitung terpisah, seperti:
I = Isilinder + Ikerucut
![]()
Diketahui:
ms = 2 kg dan Rs = 0,1 m;
m2 = 2 kg dan Rk = 0,1 m;
Sehingga diperoleh besar inersia benda tersebut adalah:

4. Tentukan nilai inersia pada bola pejal dengan massa 15 kg sert jari – jari 0,1 meter, apabila sumbu rotasi berada di pusat bola, sebagaimana pada gambar dibawah ini!
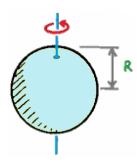
Jawab:
Inersia terhadap bola pejal sumbu rotasi berada di pusat yaitu:
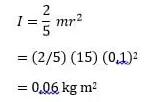
5. Tentukan inersia dari cakram pejal (padat) dengan massa 10 kg serta jari – jari 0,1 meter, apabila sumbu rotasi berada di pusat cakram, sebagaimana yang ditunjukkan pada gambar di bawah ini!
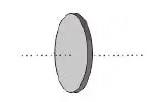
Jawab:
Cakram pejal di atas mempunyai inersia sebesar: