Pembagian Pecahan

Pecahan merupakan suatu bilangan yang dapat dibentuk a/b, di mana b≠0. Yang mana dalam hal ini (a) biasa disebut juga sebagai pembilang serta b disebut sebagai penyebut. Dan kali ini kita akan membahas mengenai operasi pecahan, mulai dari penjumlahan hingga pembagian pecahan.

Bilangan pecahan memiliki bentuk a/b .

Pada saat kita membagikan pecahan terdapat beberapa ketentuan yang berbeda dari bilangan bulat, di mana dalam pembagian pecahan memakai operasi perkalian pecahan.

Jenis Jenis Bilangan Pecahan

Berikut merupakan beberapa jenis dari bilangan pecahan, antara lain:

Pecahan Biasa

Pecahan biasa merupakan pecahan yang hanya terdiri dari pembilang dan penyebut.

Sebagai contoh:

Pecahan Campuran

Pecahan campuran merupakan bilangan pecahan yang terdiri dari pecahan bilangan bulat, pembilang, dan juga penyebut.

Sebagai contoh:

Pecahan Desimal

Pecahan desimal merupakan bilangan yang diperoleh dari hasil pembagian pada sebuah bilangan dengan 10, 100, 1000 dan seterusnya.

Pecahan desimal pada umumnya ditandai dengan penggunaan tanda koma (,).

Sebagai contoh:

1. 0,3 = lima persepuluh ⇒ didapatkan dari 3 dibagi 10.
2. 0,50 = lima puluh perseratus ⇒ didapatkan dari lima puluh dibagi seratus.

Pecahan Persen

Pecahan persen merupakan sebuah bilangan yang dibagi seratus.

Sebagai contoh:

1. 20% dibaca 20 persen serta nilainya sama dengan 20 per 100 = 0,2
2. 45% dibaca 45 persen serta nilainya sama dengan 45 per 100 = 0,45

Pecahan Permil

Pecahan permil adalah sebuah bilangan yang dibagi dengan seribu.

Sebagai contoh:

1. 10‰ dibaca 10 permil serta nilainya sama dengan 10 per 1000 = 0,01
2. 70‰ dibaca 70 permil serta nilainya sama dengan 70 per 1000 = 0,07

Pecahan Senilai

Pecahan disebut mempunyai nilai yang sama apabila pembanding dan penyebut bisa dikali ataupun dibagi dengan angka yang sama.

Menyederhanakan Pecahan

Cara menyederhanakan bilangan pecahan bisa dengan menerapkan pembagian pada pembilang dan penyebut  dengan bilangan yang bernilai sama.

Sebagai contoh:

Sederhanakanlah bentuk dari 9/27!

Tahapan Penyederhanaan

• Membagi penyebut dan pembilang dengan bilangan yg sama di mana 9/27 dibagi dengan bilangan 3 sehingga akan kita peroleh 3/9.
• Sebab masih dapat kita sederhanakan (bisa dibagi) maka bilangan tersebut masih dapat kita bagi atau disederhanakan. Apabila tidak bisa dibagi lagi maka bilangan tersebut sudah merupakan bilangan sederhana. Dalam soal di aatas, 3/9 masih bisa dibagi dengan bilangan tiga, sehingga kita peroleh 1/3.
• Untuk menentukan bilangan pembagi dalam penyederhaan dapat dengan bilangan yang terkecil dan mungkin dapat membagi pembilang dan penyebut. Atau juga dapat dengan mencari nilai FBP dari kedua bilangan (pembilang dan penyebut).

Operasi Hitung Pecahan

Penjumlahan

Cara menghitung penjumlahan pada pecahan yakni dengan melihat penyebutnya terlebih dahulu. Apabila sama maka jumlahkan pembilangnya.

Sehingga hasilnya merupakan jumlah dari pembilang dibagi dengan penyebut soal yang diketahui. Apabila penyebutnya berbeda maka disamakan terlebih dahulu penyebutnya.

Contoh 1:

Hitunglah operasi bilangan di bawah ini:

Jawab:

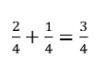
Contoh 2:

Hitunglah operasi bilangan di bawah ini:

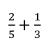
Jawab:

Untuk menyamakan penyebut kita pakai KPK dari kedua bilangan penyebutnya

KPK dari 5 dan 3 yaitu 15, sehingga:

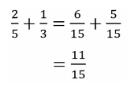
Pengurangan

Cara menghitung pengurangan pada bilangan pecahan yakni dengan cara menyamakan penyebut dari pecahan yang akan dioperasikan. Apabila penyebut telah sama maka kurangkan pembilangnya.

Untuk menyamakan penyebut kita memakai KPK dari kedua bilangan penyebut pecahan

Sebagai contoh:

Hitunglah operasi bilangan di bawah ini:

Jawab:

KPK dari 7 dan 2 yaitu 14, sehingga:

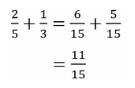
Perkalian

Untuk mengalikan dua bilangan pecahan yakni dengan cara mengalikan penyebut dengan penyebut serta mengalikan pembilang dengan pembilang.

Sebagai contoh:

Hitunglah operasi bilangan di bawah ini:

Jawab:

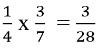
Pembagian

Dalam bagian pembagian ini, kita akan membahas mengenai embagian pecahan biasa, campuran, dan desimal. Selengkapnya, simak pembahasan berikut ini.

1. Pembagian Pecahan Biasa

Membagi pecahan biasa dengan pecahan biasa cukup hanya dengan menggunakan tahapan seperti uraian rumus perkalian pecahan.

Namun bedanya pada pembagian di balik antara penyebut dan pembilangnya, dan kemudian barulah berlaku operasi kali.

Sebagai contoh:

Soal 1.

Jawab:

Langkah pertama adalah membalik pecahan pembagi, ketika pecahan pembagi telah dibalik maka operasi bagi berubah menjadi operasi kali sehingga akan berubah bentuknya menjadi seperti di bawah ini:

Sesudah berubah menjadi operasi kali maka berikutnya adalah operasikan pembilang di kali pebilang. Kemudian penyebut dikali dengan penyebut.

Sehingga kita peroleh 14/7 yang mana hasil dari pembagian di atas masih bisa kita sederhanakan lagi menjadi 14/7 = 2 .

Konsep penyederhanaan pecahan adalah dengan cara membagi pecahan pembilang dan juga penyebut dengan bilangan yang sama 14 : 7 =2.

Lalu penyebut 7 : 7 =1 hingga di bisa penyederhanaannya 2/1 dalam pecahan biasanya per satu tidak di tulisakan, Sehingga akan ditulis 2.

Soal 2.

Carilah hasil pembagian pecahan di bawah ini:

Jawab:

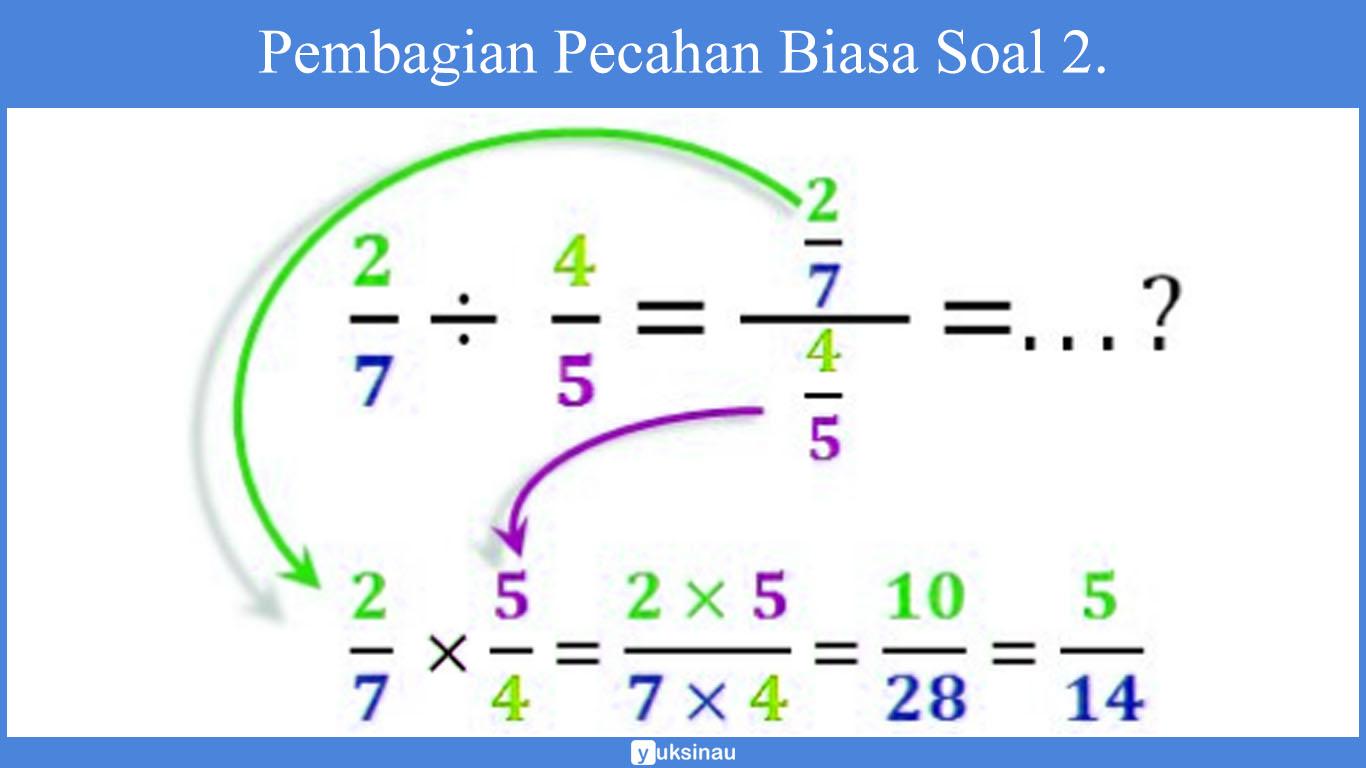
Sama seperti contoh pada soal 1 sebelumnya pembagi adalah 4/5 di balik menjadi 5/4.

Kemudian berlaku operasi perkalian, pembilang kali dengan pembilang 2 x5, penyebut dikali dengan penyebut 7 x 4 sehingga akan kita peroleh 10/28.

Sebab masih dapat di sederhanakan maka bagi pembilang dan penyebut dengan bilangan sama yakni di bagi 2 sehingga di dapat 5/14

2. Pembagian Pecahan Campuran

Pecahan campuran merupakan pecahan yang terdiri atas bilangan bulat dan juga bilangan pecahan contohnya : 5 2/3.

Kunci dari pembagian pecahan campuran yaitu dengan cara pecahan campuran diubah terlebih dahulu menjadi pecahan biasa.

Sebagai contoh:

Soal 1.

Tentukan hasil pembagian dari pecahan di bawah ini:

Jawab:

Langkah pertama yaitu dengan cara mengubah pecahan campuran sampai menjadi pecahan biasa.

Yakni dengan cara mengalikan penyebutnya dengan bilangan bulat lalu kemudian di tambah pembilang, hasilnya di letakkan sebagai pembilang dan juga penyebutnya tetap.

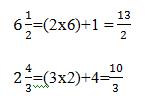
Kita telah peroleh pecahan 13/2 dan 10/3. sampai 13/2 : 10/3

Langkah selanjutnya sama dengan pengoperasian pembagian pecahan biasa, sehingga:

13/2 x 3/10 = (13×3)/(2×10) = 39/20

3. Pembagian Pecahan Desimal

Pembagian pecahan desimal merupakan pecahan dengan peyebut, 10, 100, 1000, 10000 dan begitu juga seterusnya.

Penyebut di identifikasi lewat jumlah angka di belakang koma, 1 bilangan di belakang koma menjadi penyebutnya 10, andai ada 2 bilangan di belakang koma maka akan menjadi penyebutnya 100, andai 3 maka akan menjadi penyebutnya 1000 dan begitu juga seterusnya.

Sebagai contoh:

Soal 1.

Selesaikan pembagian desimal berikut ini: 0,66 : 0,02 = … ?

Jawab:

Langkah yang pertama adalah mengubah desimal ke dalam bentuk pecahan biasa, sehingga akan menjadi:

0,66 = 66 / 100 = 33/50

0,02 = 2 / 100 = 1/50

Apabila telah kita peroleh pecahan biasa yakni 33/50 dan 1/50 disebabkan kedua desimal itu mengandung 2 angka di belakang koma sehingga penyebutnya adalah 100.

Lalu operasikan seperti pembagian pecahan biasa, menjadi:

= 33 / 50 : 1/50
= 33 / 50 x 50/1 = 33

Soal 2.

Selesaikan pembagian bilangan desimal berikut ini: 2,4 : 0,2 = …

Jawab:

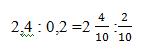
Ubah dahulu desimal menjadi pecahan, sehingga akan kita dapatkan pecahan campuran, kemudian lakukan seperti langkah pada pembagian pecahan campuran yakni dengan cara mengubah pecahan campuran menjadi pecahan bisa dengan mengalikan penyebut dengan bilangan bulatnya.

Kemudian dijumlahkan dengan pembilang. (10 x 2)+4 =24, sehingga akan kita peroleh 24/10.

Demikianlah ulasan singkat mengenai Pecahan yang dapat kami sampaikan. Semoga ulasan di atas  dapat kalian jadikan sebagai bahan belajar kalian.