Bentuk Aljabar

Taukah kamu apa itu aljabar? Bentuk aljabar merupakan suatu bentuk dari matematika di mana dalam penyajiannya memuat berbagai huruf untuk mewakili bilangan yang belum diketahui.

Bentuk aljabar biasa digunakan dalam menyelesaikan masalah pada kehidupan sehari-hari.

Berbagai hal yang tidak atau belum diketahui seperti banyaknya bahan bakar minyak yang diperlukan oleh sebuah bis dalam setiap minggunay, jarak yang ditempuh dalam waktu tertentu, ataupun banyaknya makanan ternak yang diperlukan dalam kurun waktu 3 hari.

Hal itu semua bisa kita cari hasilnya dengan memakai bentuk aljabar. Informasi selengkapnya mengenai aljabar simak pembahasan berikut ini.

Unsur Unsur Aljabar

Berbagai bentuk kalimat matematika seperti 2a , -5b, x3, 3p + 2q biasa dikenal dengan sebuatan bentuk aljabar.

Dalam bentuk aljabar 2a,2 , angka tersebut dinamakan koefisien, sementara untuk a disebut sebagai variabel atu juga bisa disebut sebagai peubah.

Sedangkan untuk bentuk 5x² + 13x + 6 disebut sebagai bentuk aljabar suku dua atau binom. Dan bentuk 8x² – 26xy + 15y² disebut sebagai bentuk aljabar suku tiga atau  trinom.

Dari ulasan singkat di atas, kita sudah mengetahui beberapa unsur yang ada di aljabar. Untuk mempermudah pemahaman kalian, berikut akan kami berikan informasi detailnya untuk masing-masing unsur. Simak baik-baik ulasan berikut ini.

1. Variabel

Variabel merupakan suatu lambang sebagai pengganti pada suatu bilangan yang belum diketahui nilainya dengan jelas.

Variabel juga memiliki sebutan lain yakni peubah. Variabel pada umumnya dilambangkan dengan penggunaaan huruf kecil a, b, c, … z.

Sebagai contoh:

Sebuah bilangan apabila kita kalikan 5 lalu dikurangi 3, hasilnya akan berjumlah 12. Buatlah bentuk persamaannya!

Jawab:

Misalnya, bilangan tersebut x, yang artinya 5x – 3 = 12. (di mana x adalah variabelnya)

2. Konstanta

Suku dari suatu bentuk aljabar yang berwujud bilangan serta tidak memuat variabel disebut sebagai konstanta.

Sebagai contoh:

Tentukan konstanta dari bentuk aljabar di bawah ini:

a. 2 x² + 3xy + 7x – y – 8
b. 3 – 4 x² – x

Jawab: 

a. Konstanta merupakan suku yang tidak memuat variabel, sehingga konstanta dari 2 x² + 3xy + 7x – y – 8
tidak lain yaitu –8.

b. Konstanta dari 3 – 4 x² – x yaitu 3.

3. Koefisien

Koefisien dalam bentuk aljabar merupakan suatu faktor konstanta dari sebuah suku dalam bentuk aljabar.

Sebagai contoh:

Tentukan koefisien x dari bentuk aljabar di bawah ini:

a. 5x²y + 3x

b. 2x²+ 6x – 3

Jawab:

a. Koefisien x dari 5 x²y + 3x yaitu 3.

b. Koefisien x dari 2 x² + 6x – 3 yaitu 6. 

4. Suku Sejenis dan Suku Tak Sejenis

1. Suku

Yang dimaksud suku dalam aljabar merupakan suatu variabel beserta koefisiennya atau konstanta dalam bentuk aljabar yang dipisahkan oleh operasi jumlah atau selisih.

Suku dalam aljabar di bagi menjadi dua macam, yakni suku sejenis dan suku tak sejenis, berikut informasi selengkapnya.

Suku-suku sejenis merupakan suatu suku yang mempunyai variabel serta pangkat dari masing-masing variabel yang sama.

Sebagai contoh:

5x dan –2x, 3a2 dan a2, y dan 4y, …

Sedangkan, suku tak sejenis merupakan suatu suku yang mempunyai variabel dan pangkat dari masing-masing variabel yang tidak sama.

Sebagai contoh:

2x dan –3×2, –y dan –x3, 5x dan –2y, …

2. Suku Satu

Suku satu dalam aljabar merupakan bentuk aljabar yang tidak dihubungkan oleh operasi jumlah atau selisih.

Sebagai contoh:

3x, 2a2, –4xy, …

3. Suku Dua

Yang dimaksud suku dua dalam aljabar yaitu bentuk aljabar yang dihubungkan oleh satu operasi jumlah atau selisih.

Sebagai contoh:

2x + 3, a2 – 4, 3×2 – 4x, …

4. Suku Tiga

Suku tiga merupakan bentuk aljabar yang dihubungkan oleh dua operasi jumlah atau selisih.

Sebagai contoh:

2×2 – x + 1, 3x + y – xy, …

Bentuk aljabar yang memiliki lebih dari dua suku disebut sebagai suku banyak.

Operasi Hitung dalam Al jabar

Berikut akan kami berikan penjelasan operasi hitung seperti penjumlahan, pengurangan, perkalian, pembagian dan lainnya dalam bentuk aljabar. Perhatikan baik-baik ulasan di bawah ini ya.

1. Penjumlahan dan Pengurangan Bentuk Aljabar

Dalam bentuk aljabar, operasi penjumlahan dan juga pengurangan hanya bisa dilakukan pada suku-suku yang sejenis atau sama.

Kita hanya perlu untuk menjumlahkan atau mengurangkan koefisien pada suku-suku yang sejenis.

Agar lebih jelas, liat contoh soal di bawah ini:

Tentukan hasil penjumlahan dan juga pengurangan pada bentuk aljabar di bawah ini:

a. –4ax + 7ax

b. (2x² – 3x + 2) + (4x² – 5x + 1)

c. (3a² + 5) – (4a² – 3a + 2)

Jawab:

a. –4ax + 7ax = (–4 + 7)ax = 3ax

b.
(2x² – 3x + 2) + (4x² – 5x + 1)
= 2x² – 3x + 2 + 4x² – 5x + 1
= 2x² + 4x² – 3x – 5x + 2 + 1
= (2 + 4)x² + (–3 – 5)x + (2 + 1)
= 6x² – 8x + 3

c.
(3a² + 5) – (4a² – 3a + 2)
= 3a² + 5 – 4a² + 3a – 2
= 3a² – 4a² + 3a + 5 – 2
= (3 – 4)a² + 3a + (5 – 2)
= – a²+ 3a + 3

2. Perkalian

Perlu kalian ingat kembali jika dalam perkalian bilangan bulat akan berlaku sifat distributif perkalian kepada penjumlahan.

Di mana a × (b + c) = (a × b) + (a × c) serta sifat distributif perkalian pada pengurangan adalah a × (b – c) = (a × b) – (a × c).

Sehingga, untuk masing-masing bilangan bulat a, b, dan c. Sifat ini akan berlaku pada perkalian bentuk aljabar.

Berikut akan kami berikan beberapa jenis perkalian yang ada di dalam bentuk perkalian aljabar.

a. Perkalian antara konstanta dengan bentuk aljabar

Perkalian suatu bilangan konstanta k dengan bentuk aljabar suku satu serta suku dua dinyatakan seperti di bawah ini:

k(ax) = kax

k(ax + b) = kax + kb

Sebagai contoh:

Uraikan bentuk aljabar di bawah ini, lalu sederhanakanlah!

a. 4(p + q)
b. 5(ax + by)
c. 3(x – 2) + 6(7x + 1)
d. –8(2x – y + 3z)

Jawab:

a. 4(p + q) = 4p + 4q

b. 5(ax + by) = 5ax + 5by

c.
3(x – 2) + 6(7x + 1) = 3x – 6 + 42x + 6
= (3 + 42)x – 6 + 6
= 45x

d. –8(2x – y + 3z) = –16x + 8y – 24z

b. Perkalian antara dua bentuk aljabar

Seperti pada perkalian sebuah konstanta dengan bentuk aljabar, untuk mencari hasil kali antara dua bentuk aljabar kita bisa menggunakan sifat distributif perkalian pada penjumlahan. Serta juga dapat menggunakan sifat distributif perkalian terhadap pengurangan.

Selain dengan menggunakan metode atau cara tersebut, untuk mencari hasil kali antara dua bentuk aljabar. Kita juga bisa memakai cara atau metode sebagai berikut.

Perhatikan perkalian antara bentuk aljabar suku dua dengan suku dua di bawah ini:

(ax+b)(cx+d) = ax × cx + ax × d + b × cx + b × d

          = acx² + (ad +bc)x + bd

Selain dengan metode skema seperti yang tertera di atas, untuk mengalikan bentuk aljabar suku dua dengan suku dua kita juga dapat memakai sifat distributif seperti uraian di bawah:

(ax+b)(cx+d) = ax(cx +d) + b(cx +d)

= ax × cx +ax × d + b × cx + b × d

= acx² +adx +bcx +bd

 = acx² +(ad + bc)x + bd

3. Perpangkatan

Masih ingatkah kalian mengenai operasi perpangkatan pada bilangan bulat?

Operasi perpangkatan didefinisikan sebagai perkalian berulang pada bilangan yang sama.

Hal tersebut ternyata juga berlaku pada perpangkatan bentuk aljabar lho. Dalam perpangkatan bentuk aljabar suku dua, koefisien masing-masing suku akan ditentukan berdasarkan segitiga Pascal.

Sebagai contoh, kita akan menentukan pola koefisien pada penjabaran bentuk aljabar suku dua (a + b)n, dengan n merupakan bilangan asli.

Perhatikan baik-baik ulasan di bawah ini:

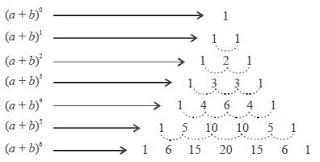
Dalam uraian di atas mengenai segitiga Pascal, bilangan yang terletak di bawahnya didapatkan dari penjumlahan bilangan yang berdekatan yang letaknya di atasnya.

4. Pembagian

Hasil bagi dua dalam bentuk aljabar bisa kita dapatkan dengan cara menentukan terlebih dahulu faktor dari sekutu masing-masing dari bentuk aljabar tersebut.

Lalu kita lakukan pembagian pada pembilang dan juga penyebutnya.

Sebagai contoh:

9x : 3 = 9x/3 = 3x
15pq : 5q = 15pq / 5 q = 3p

Pembagian bentuk aljabar akan lebih mudah dilakukan apabila kita ubah bentukan ke dalam bentuk pecahan.

5. Substitusi pada Bentuk Aljabar

Nilai dari sebuah bentuk aljabar bisa kita cari dengan cara menyubstitusikan sebarang bilangan pada variabel-variabel bentuk dari aljabar tersebut.

6. Menentukan KPK dan FPB Bentuk Aljabar

Masih ingatkah kalian cara untuk menentukan KPK dan FPB dari dua ataupun lebih bilangan bulat?

Hal tersebut juga berlaku pada bentuk aljabar lho.

Untuk mencari KPK dan juga FPB pada bentuk aljabar bisa kita lakukan dengan cara menyatakan bentuk-bentuk aljabar tersebut menjadi perkalian faktor-faktor primanya.

7. Perpangkatan Bentuk Aljabar

Materi pangkat sebetulnya telah kita pelajari di kelas 7 SMP. Pada intinya sama, bilangan pangkat didefinisikan sebagai berikut ini:

aⁿ = a x a x a x … x a (a sebanyak n)

Contoh soal apabila diaplikasikan dalam bentuk aljabar:

(2a)³ = 2a x 2a x 2a = 2 x 2 x 2 x a x a x a = 8a³
(4x²y)² = 4x²y x 4x²y = 16 x⁴ y²

• (a+b)² = a² + 2ab + b²
• (a-b)² = a² – 2ab + b²

Pecahan dalam bentuk Al jabar

1. Pengurangan dan Penjumlahan Pecahan dalam Bentuk Aljabar

Sebetulnya prinsipnya sama dengan cara menjumlahkan dan mengurangkan pecahan bentuk aljabar. Di mana pengurangan dan penjumlahannya sama dengan menjumlahkan dan mengurangkan pada pecahan biasa.

Yakni dengan cara menyamakan penyebutnya terlebih dahulu.

Perhatikan baik-baik contoh soal di bawah ini:

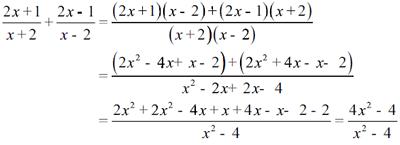
Sementara untuk operasi pengurangan perhatikan contoh di bawah ini:

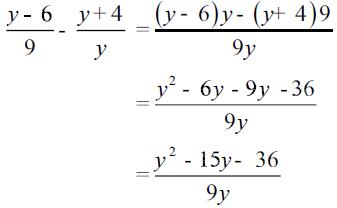
2. Perkalian dan Pembagian Bentuk Aljabar

a. Perkalian

Caranya hampir sama dengan yang ada pada perkalian pecahan. Pembilang kali pembilang, penyebut kali penyebut kemudian kita sederhanakan apabila terdapat bilagan yang bisa disederhanakan.

Rumusnya:

Sebagai contoh:

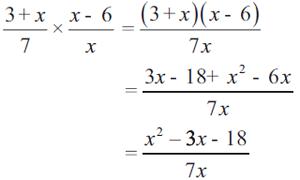
b. Pembagian

Cara pembagian pecahan dalam bentuk aljabar sama dengan pembagian yang ada pada bilangan pecahan biasa.

Kalian dapat mengubahnya ke bentuk perkalian dengan membalik pecahan aljabar pembagi.

Rumusnya:

Sebagai contoh:

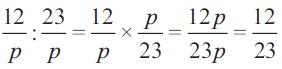
c. Penyederhanaan Pecahan bentuk Aljabar

Untuk dapat menyederhanakan pecahan dalam bentuk aljabar kalian harus memegang prinsip. Prinsipnya di mana pada saat ada faktor persekutuan yang sama antara pembilang dan penyebut maka dapat kita sederhanakan.

Faktor persekutuan dapat berwujud angka ataupun variable dengan jenis dan pangkat yang sama.

Perhatikan contoh berikut ini:

Sederhanakan pecahan berikut:

10p/24pr

Dari pecahan di atas, terdapat faktor persekutuan yang sama antara pembilang dan penyebut yakni 2p. Faktor persekutuan ini kita coret sehingga akan berubah menjadi:

10p/24pr = 2p . 5 / 2p . 12 r = 5/12r

Dalam beberapa kasus soal pada umumnya penyederhanaan pecahan dilakukan dengan terlebih dahulu melakukan pemfaktoran.

Sebagai contoh:

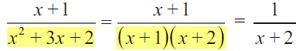
Pemfaktoran Bentuk Aljabar

1. Pemfaktoran menggunakan Sifat Distributif

Contoh:

Coba kalian cari faktor dari  5ab + 10b

Untuk mencari faktor dari 5ab + 10b pertama yang harus kalian lakukan adalah mencari faktor persekutuan terbesar (FPB) dari 5 dan 10 serta dari ab dan b.

FPB dari 5 dan 10 yaitu 5 serta persekutuan terbesar ab dan b yaitu b. Sehingga kita keluarkan 5b.

5ab + 10b = 5b (a+2b)

2. Pemfaktoran Selisih Dua Kuadrat

Yang disebut sebagai bentuk selisih dua kuadrat yaitu:

a² – b² = (a+b) (a-b)

Sebagai contoh:

25x² – y² = (5x + y) (5x – y)
20p² – 5q² = 5 (4p² – q²) = 5 (2p + q) (2p – q)

3. Pemfaktoran Bentuk Kuadrat

a. Pemfaktoran ax² + bx + c dengan a = 1

Bentuk aljabar kuadrat x² + (p + q)x + pq bisa kita faktorkan menjadi (x + p) (x + q).

Sebagai contoh:

x² + (p + q)x + pq = ax² + bx + c sehingga akan menjadi:

a = 1, b = p + q,dan c = pq.

Dari contoh di atas, bisa kita lihat jika p dan q adalah faktor dari c.

Apabila p dan q dijumlahkan, hasilnya yaitu b. Dengan begitu, untuk memfaktorkan bentuk ax2 + bx + c dengan a = 1, tentukan dua bilangan yang merupakan faktor dari c. Serta jika kedua bilangan tersebut dijumlahkan, hasilnya sama dengan b.

Contoh:

x2 + 5x + 6 = (x + …) (x + …)

Misalnya, x² + 5x + 6 = ax² + bx + c, didapatkan a = 1, b = 5, dan c = 6.

Untuk mengisi titik-titik, tentukan dua bilangan yang merupakan faktor dari 6 serta jika kedua bilangan tersebut dijumlahkan, hasilnya akan sama dengan 5.

Faktor dari 6 yaitu 6 dan 1 atau 2 dan 3, yang memenuhi syarat yakni 2 dan 3 karena 2 + 3 = 5

Sehingga, x² + 5x + 6 = (x + 2) (x + 3).

b. Pemfaktoran Bentuk ax² + bx + c dengan a ≠ 1

Sebelumnya, kalian sudah memfaktorkan bentuk ax² + bx + c dengan a = 1. Sekarang kalian akan mempelajari cara memfaktorkan bentuk ax² + bx + c dengan a ≠ 1.

Perhatikan contoh di bawah ini:

(x + 3) (2x + 1) = 2x² + x + 6x + 3

= 2x² + 7x + 3

Dengan kata lain, bentuk dari 2x² + 7x + 3 jika kita faktorkan akan menjadi (x + 3) (2x + 1). Adapun cara memfaktorkan 2×2 + 7x + 3 yaitu dengan cara membalikkan tahapan perkalian suku dua di atas.

2x² + 7x + 3
= 2x² + (x + 6 x) +3
= (2x² + x) + (6x + 3)
= x (2x + 1) + 3(2x + 1)
= (x + 3)(2x+1)

Dari uraian di atas dapat kita simpulkan bahwa untuk melakukan pemfaktoran ax² + bx + c dengan a ≠ 1 bisa kita lakukan dengan menggunakan tahapan sebagai berikut:

1. Uraikan bx menjadi penjumlahan dua suku yang jika kedua suku tersebut dikalikan akan menghasilkan nilai yang sama dengan (ax²)(c). –> b = a x c
2. Faktorkan bentuk yang didapatkan pada langkah 1 dengan memakai sifat distributif perkalian terhadap penjumlahan atau pengurangan.

2x² + 11x + 12
= 2x² + 3x + 8x + 12
(11 diuraikan 3 dan 8, 3 x 8 = 2 x 12)
= (2x² + 3x) + (8x + 12)
= x(2x + 3) + 4(2x + 3)
= (x + 4)(2x + 3)

Contoh Soal dan Pembahasan

Penjumlahan dan Pengurangan Aljabar 

Soal 1.

Tentukan bentuk sederhana dari:

4(3x + 2) – 3(6x – 5)

Jawab:

4(3x + 2) – 3(6x – 5)
= 4.3x + 4.2 – (3.6x – 3.5)
= 12x + 8 – (18x – 15)
= 12x + 8 – 18x + 15
= 12x – 18x + 8 + 15
= -6x + 23

Soal 2.

Faktorkan bentuk-bentuk berikut:

a) 25x + 20y

b) 2mn − 8m

c) 15xy² + 10x²y

d) 6ab²c³ − 18 a³c²

e) 4xy²z³ + 6x²y³z²  + 12x³yz²

f) 4xy²z³ + 6x²y³z²

Jawab:

Soal-soal di atas adalah tipe distributif, sehingga cara pemfaktorannya tinggal kita ringkas saja menjadi :

a) 25x + 20y
= 5(5x + 4y)

b) 2mn − 8m
= 2m(n − 4)

c) 15xy² + 10x²y
= 5xy (3y + 2x)

d) 6ab²c³ − 18 a³c²
= 6ac² (b²c + 3a²)

e) 4xy²z³ + 6x²y³z²  + 12x³yz²
= 2xyz (2yz² + 3xy²z + 6x²z)

f) 4xy²z³ +  12x³yz²
= 2xyz (2yz²  + 6x²z)

Soal 3.

Tulislah bentuk sederhana dari bilangan di bawah ini:

6x² + x – 2 / 4x² – 1 ?

Jawab:

Pemfaktoran dari pembilangnya yaitu:

6x² + x – 2 = 6x² – 3x + 4x – 2

= 3x ( 2x – 1 ) + 2 ( 2x – 1 )

= ( 3x + 2 ) ( 2x – 1 )

Pemfaktoran dari penyebutnya:

4x² – 1 = ( 2x + 1 ) ( 2x – 1 )

Sehingga akan kita dapatkan bentuk bilangan seperti:

6x² + x – 2 / 4x² – 1 = ( 3x + 2 ) ( 2x – 1 ) / ( 2x + 1 ) ( 2x – 1 )

Lalu kita hilangkan faktor yang sama antara penyebut dan pembilang nya, yaitu 2x – 1. Sehingga akan didapatkan sebuah hasil akhir seperti di bawah ini:

6x² + x – 2 / 4x² – 1 = 3x + 2 / 2x + 1

Sehingga, hasil bentuk sederhana dari bilangan 6x² + x – 2 / 4x² – 1 adalah: 3x + 2 / 2x + 1.

Soal 4.

Berapakah hasil dari bilangan di bawah ini:

( 2x + 3 ) ( 4x – 5 )?

Jawab:

( 2x + 3 ) ( 4x – 5 ) = 2x ( 4x – 5 ) + 3 ( 4x – 5 )

= 8x² – 10x + 12x – 15

= 8x² + 2x – 15

Sehingga, hasil dari bilangan ( 2x + 3 ) ( 4x – 5 ) adalah: 8x² + 2x – 15.

Soal 5.

Tulislah bentuk sederhana dari bilangan di bawah ini:

3x² – 13x – 10 / 9x² – 4 ?

Jawab:

Pemfaktoran dari pembilangnya yaitu:

3x² – 13x – 10 = 3x² – 15x + 2x – 10

= 3x ( x – 5 ) + 2 ( x – 5 )

= ( 3x + 2 ) ( x – 5 )

Pemfaktoran dari penyebutnya yaitu:

9x² – 4 = ( 3x + 2 ) ( 3x – 2 )

Sehingga akan kita dapatkan bentuk bilangan:

3x² – 13x – 10 / 9x² – 4 = ( 3x + 2 ) ( x – 5 ) / ( 3x + 2 ) ( 3x – 2 )

Lalu hilangkan faktor yang sama antara pembilang dan penyebutnya yaitu 3x + 2. Sehingga, akan kita dapatkan hasil akhir seperti di bawah ini:

3x² – 13x – 10 / 9x² – 4 = x – 5 / 3x – 2

Sehingga, hasil bentuk sederhana dari bilangan 3x² – 13x – 10 / 9x² – 4 adalah: x – 5 / 3x – 2.

Demikianlah ulasan singkat kali ini yang dapat kami sampaikan. Semoga ulasan di atas dapat kalian jadikan sebagai bahan belajar kalian.