Bilangan Berpangkat – Eksponen

Mungkin dari sebagian kalian telah mempelajari mengenai materi bilangan berpangkat. Atau mungkin belum pernah mendengar sama sekali apa itu bilangan berpangkat. Berikut informasi selengkapnya.

Materi bilangan berpangkat ini ternyata mempunyai banyak manfaat ataupun kegunaan yang sangat penting khususnya bagi para ilmuan-ilmuan.

Informasi selengkapnya mengenai bilangan berpangkat, simak pembahasan berikut ini.

Bilangan Berpangkat

Bilangan berpangkat merupakan suatu bilangan yang berguna untuk menyederhanakan penulisan serta penyebutan suatu bilangan yang mempunyai faktor-faktor perkalian yang sama.

Sebagai contoh: 3x3x3x3x3=… atau 7x7x7x7x=… , dan lain sebagainya.

Perkalian berbagai bilangan dengan faktor-faktor yang sama seperti di atas pada umumnya disebuat dengan perkalian berulang.

Bayangkan apabila yang dikalikan angkanya sangat banyak, maka kita juga akan mengelami kesulitan di dalam dalam penulisannya.

Hal tersebut tak lain sebab sangking banyaknya angka untuk satu kali bilangan pada perkalian tersebut.

Masing-masing perkalian berulang bisa kita tuliskan secara ringkas dengan memakai notasi angka bilangan berpangkat.

Sebagai contoh:

3 x 3 x 3 x 3 x 3 bilangan tersebut bisa kita ringkas kembali dengan memakai bilangan berpangkat menjadi 3⁵

8 x 8 x 8 x 8 x 8 x 8 x 8 x 8 x 8 x 8 dan angka tersebut bisa kita ringkas kembali hingga menjadi bilangan berpangkat 8¹⁰

Cara membacanya:

3⁵: Sepuluh pangkat 5

 8¹⁰ : Delapan pangakt 10

Pangkat di atas berguna untuk menentukan jumlah faktor yang di ulang.

Rumus bilangan berpangkat yaitu:

aⁿ=a×a×a×a…sebanyak n kali

Jenis  Jenis Bilangan Berpangkat

Terdapat beberapa jenis bilangan berpangkat yang paling sering dibahas.

Antara lain yakni: bilangan berpangkat positif (+), bilangan berpangkat negatif (-) serta bilangan berpangkat nol (0).

Berikut akan kami berikan penjelasan pada masig-masing jenisnya. Simak baik-baik ulasan di bawah ini ya.

1. Bilangan Berpangkat Positif

Bilangan berpangkat positif merupakan suatu bilangan yang mempunyai pangkat atau eksponen positif.

Apa itu yang dimaksud sebagai eksponen? eksponen merupakan penyebutan lain dari pangkat. Bilangan berpangkat positif mempunyai sifat-sifat tertentu, yang mana bilangan tersebut terdiri atas a, b, sebagai bilangan real dan m, n, yang merupakan bilangan bulat positif.

Bilangan Eksponen merupakan suatu bentuk pada bilangan perkalian dengan bilangan yang sama kemudian di ulang-ulang atau pengertian singkatnya yaitu perkalian yang diulang-ulang.

Adapun beberapa sifat dari bilangan berpangkat positif, diantaranya ialah sebagai berikut ini:

1. a^m x aⁿ = a^m+n
2. a^m : aⁿ = a^{m-n ,} untuk m>n dan b ≠ 0
3. (a^m)ⁿ = a^mn
4. (ab)^m = a^m b^m
5. (a/b)^m = a^m/b^m , untuk b ≠ 0

Untuk lebih memahami uraian di atas, perhatikan baik-baik contoh soal di bawah ini.

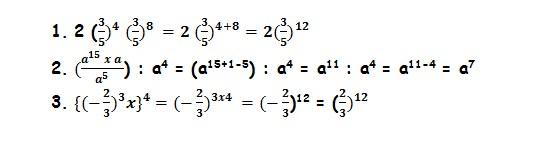
2. Bilangan Berpangkat Negatif

Kemudian ialah pengertian dari bilangan berpangkat negatif yang merupakan bilangan yang mempunyai pangkat atau eksponen negatif (-).

Adapun beberapa sifat bilangan berpangkat negatif, antara lain ialah sebagai berikut:

Jika a∈R, a ≠ 0, dan n merupakan bilangan bulat negatif, maka:

a^-n = 1/aⁿ atau aⁿ = 1/ a^-n

Untuk lebih memahami uraian di atas, perhatikan baik-baik contoh soal di bawah ini:

Soal 1.

Tentukan sekaligus nyatakan dengan pangkat positif bilangan berpangkat di bawah ini:

1/ 6(a + b)^-7 = ….

Jawab:

1/ 6(a + b)^-7 = = 1/6 (a+b)⁷

Soal 2.

Nyatakan dengan pangkat negatif bilangan berpangkat di bawah ini:

x¹y² / 2z⁶ = ….

Jawab:

x¹y² / 2z⁶ = 2^-1x^-1z^-6 / y^-2, dengan x ≠ 0 dan z ≠ 0.

3. Bilangan berpangkat Nol (0)

Tak hanya ada bilangan berpangkat positif serta bilangan berpangkat negatif yang ada pada bilangan berpangkat lho.

Ternyata, dalam ilmu matematika juga terdapa bilangan berpangkat nol (a). Maka dati itu, yuk mari kita pelajari lebih dalam mengenai bilangan berpangkat nol ini.

Sebelumnya kita sudah mengetahui bahwa sifat-sifat bilangan berpangkat, ialah sebagai berikut:

aⁿ/aⁿ = 1 berdasarkan dari sifat pembagian bilangan berpangkat positif maka bisa kita dapatkan:

aⁿ/aⁿ = a^n-n = a⁰, sehingga a⁰ = 1

Sehingga sifat dari bilangan berpangkat nol (0) yaitu “Jika nilai a merupakan bilangan riil serta a tidak sama dengan 0, maka a⁰ = 1″

Untuk lebih memahami uraian di atas, perhatikan baik-baik contoh soal di bawah ini:

Sederhanakan beberapa bilangan berpangkat di bawah ini:

Soal 1.

5(x² – y²)(x² – y²)⁰

Soal 2.

3x + 2 y / (3x + 2y)⁰

Jawab:

Soal 1.

5(x² – y²)(x² – y²)⁰ = 5(x² – y²) x 1 = 5(x² – y²), dengan x² – y²  ≠ 0

Soal 2.

3x + 2 y / (3x + 2y)⁰ = 3x + 2y / 1 = 3x + 2y, dengan 3x + 2y ≠ 0

Demikianlah pembahasan yang dapat kita sampaikan terakti bilangan berpangkat, sekarang kita lanjutkan ke pembahasan yang ke dua yakni Bentuk Akar. Perhatikan baik-baik ulasan di bawah ini ya..

Sifat Sifat Bilangan Berpangkat

Berikut ini adalah beberapa sifat yang terdapat di dalam bilangan berpangkat, antara lian yakni:

1. Pangkat Bulat positif

Pengertian:

Sebagai contohnya a bilangan real serta n bilangan bulat positif. Notasi aⁿakan menyatakan hasil kali dari bilangan a sebanyak n faktor. Sehingga dapat kita tuliskan menjadi:

aⁿ = a × a × a × … × a

Di mana : a x a x a x …. x a merupakan n faktor.

Keterangan:

• a merupakan basis bilangan berpangkat.
• n merupakan pangkat.

Sehingga, dapat kita ketahui bahwa:

1. Pada uraian di atas, maka kita sepakati, a1 cukup ditulis dengan a.
2. Tidak seluruh a⁰ dengan a bilangan real menyatakan 1. Pada saat a = 0 serta n = 0, maka aⁿ= 0⁰, maka hasilnya tidak menentu.
3. Apabila n merupakan suatu variabel sebagai eksponen dari a, maka perlu kita perhatikan semesta variabel tersebut.
   Karena aⁿ = a × a × … × a sebanyak n faktor, ini hanya berlaku pada saat semesta n ∈N.

Untuk lebih memahami uraian di atas, perhatikan baik-baik contoh soal di bawah ini:

1. 2⁴ = 2 x 2 x 2 x 2 =16
2. 3² = 3 x 3 = 9

2. Pangkat Bulat Negatif

Pengertian:

Untuk a bilangan real serta a ≠ 0, m bilangan bulat positif, maka di definisikan menjadi:

a^-m = (1/a)^m

Dari uraian di atas maka dapat dijelaskan lagi menjadi sebagai berikut:

Untuk lebih memahami uraian di atas, perhatikan baik-baik contoh soal di bawah ini:

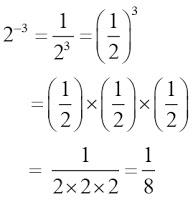
3. Pangkat Nol

Pengertian:

Untuk a bilangan real serta a ≠ 0, maka a⁰ = 1.

Kenapa a tidak boleh sama dengan nol?

Seperti yang sudah dijelaskan di atas, pada saat a = 0 maka a⁰ = 0⁰, maka hasil­nya tidak menentu.

Sebagai contoh:

• 2⁰ = 1
• 3⁰ = 1

4. Sifat-sifat Pangkat Bulat Positif

Berikut adalah beberapa sifat dari bilangan pangkat bulat positif:

Sifat-1

Apabila a bilangan real, m serta n bilangan bulat positif maka

a^m × aⁿ = a^m+n

Pembuktian:

Si­fat di atas hanya berlaku apabila a merupakan bilangan real, m serta n merupakan bi­langan bulat positif. Apabila m dan n bukan bilangan bulat positif, maka sifat-1 tidak berlaku. Contohnya: a = 0 dan m = n = 0, tidak ber­laku.

Sebagai contoh:

2² x 2³ = (2 x 2) x (2 x 2 x 2)

= 32

= 2⁵

2² x 2³ = 2²⁺³

Sifat-2

Apabila a bilangan real serta a ≠ 0, m dan n bilangan bulat positif, sehingga:

Dalam sifat-2 tidak diperkenakan apabila a = 0, karena ben­tuk perpangkatan pada sifat-2 merupakan bentuk ra­sional.

Pada pecahan yang penyebutnya tidak lazim nol. Pada a = 0 dan m, n merupakan bilangan bulat positif, sehingga a^m atau aⁿ dimung­kinkan hasilnya 0.

Apabila hasil a^m serta aⁿ keduanya nol, maka hasil baginya tidak menentu.

Apabila a^m = 0 dan aⁿ ≠ 0, maka hasil baginya 0. Namun, apabila a^m ≠ 0 dan aⁿ = 0, maka hasil baginya tak ter­definisi.

Sebagi contoh:

2⁵ / 2³ = 2 x 2 x 2 x 2 x 2 / 2 x 2 x 2

= 4

= 2²

= 2^5-3

Perpangkatan Bilangan Bulat

Secara umum, perkalian sembarang bilangan bulat a sebanyak n kali atau n faktor, yaitu:

a × a × a × … × a atau jika ditulis menjadi aⁿ

Keterangan:

a = disebut sebagai bilangan pokok atau bilangan dasar
n = disebut sebagai pangkat atau eksponen
an = disebut sebagai bilangan berpangkat (dibaca a pangkat n)

Sifat-3

Jika a bilangan real serta a ≠ 0, m dan n merupakan bilangan bulat positif, maka (a^m)ⁿ = a^mn

Pembuktian:

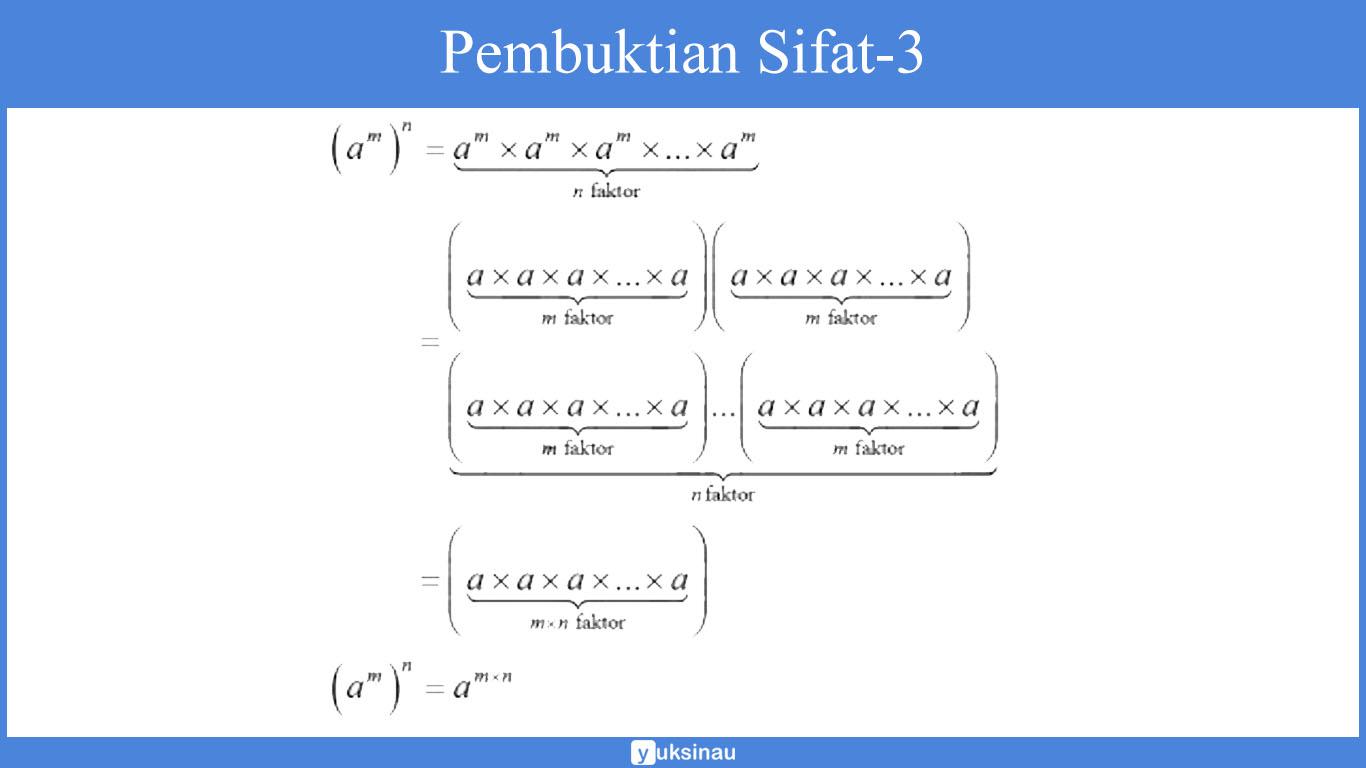
Sebagi contoh:
(2³)² = (2³) x (2³)

= (2 x 2 x 2) x (2 x 2 x 2)

= 2 x 2 x 2 x 2 x 2 x 2

= 2⁶

Di mana (2 x 2 x 2) merupakan 3 faktor, 2 x 2 x 2 x 2 x 2 x 2 merupakan 6 faktor, dan lain sebagainya.

5. Pangkat Pecahan

Pengertian:

Contohnya a merupakan bilangan real dan a ≠ 0, serta m merupakan bilangan bulat positif, maka a^1/m = p merupakan bilangan real positif, sehingga p^m = a.

Sifat-sifat perpangkatan bilangan real dengan pangkat pecahan

Pengertian:

Contonya a merupakan bilangan real dan a ≠ 0, m, n merupakan bilangan bulat positif maka didefinisikan menjadi:

a^m/n = (a^1/n)^m

Misalkan a merupakan bilangan real dengan a > 0,

p/n dan m/n merupakan bilangan pecahan n ≠ 0, maka:

(a^m/n) = (a^p/n) = (a)^m+p/n

Pembuktian:

Apabila a merupakan bilangan real dengan a > 0, sehingga:

m/n dan p/q bilangan pecahan q, n ≠ 0, maka:

(a^m/n) = (a^p/q) = (a)^m/n+p/q

Rangkuman sifat bilangan berpangkat:

Untuk a, b merupakan bilangan bulat serta n, p, dan q merupakan bilangan bulat positif, maka berlaku:

Operasi Bilangan Berpangkat

• Bilangan negatif dipangkatkan dengan pangkat ganjil maka akan menghasilakn bilangan negatif.
• Bilangan negatif dipangkatkan dengan pangkat genap maka akan menghasilkan hasilnya bilangan positif.
• Perkalian bilangan berpangkat yang bilangan pokoknya sama, maka pangkatnya akan dijumlahkan.
• Pembagian bilangan berpangkat yang bilangan pokoknya sama, maka pangkatnya akan dikurangkan.
• Sebuah bilangan berpangkat apabila dipangkatkan lagi, maka pangkatnya akan menjadi dikalikan.

Operasi Hitung Bilangan Berpangkat

Berikut akan kami berikan operasi hitung dalam bilangan berpangkat. Meliputi: sifat perkalian, pembagian, perpangkatan dan yang lainnya sekaligus contoh soal dan pembahasannya.

Perhatikan ulasan di bawah ini dengan seksama.

1. Sifat Perkalian Bilangan Berpangkat

Pada operasi hitung perkalian dalam bilangan berpangkat, berlaku sifat seperti di bawah ini:

a^m x aⁿ = a^m+n

Untuk lebih memahami cara mengenai rumus di atas, perhatikan uraian di bawah ini:

5³ x 5² = (5 x 5 x 5) x (5 x 5)

5³ x 5² = 5 x 5 x 5 x 5 x 5

5³ x 5² = 5⁵

Sehingga dapat kita simpulkan menjadi 5³ x 5² = 5⁵

Contoh Soal Sifat Perkalian Bilangan Berpangkat beserta Pembahasannya

Sederhanakan hasil perkalian dari bilangan berpangkat di bawah ini, lalu tentukan nilainya!

1. 7² x  7⁵
2. (-2)⁴ x (-2)⁵
3. (-3)³ x (-3)⁷
4. 2³ x 3⁴
5. 3y² x y³
6. 2x⁴ x 3x⁶
7. -2² x 2³

1. 7² x  7⁵  = 7²⁺⁵  = 7⁷  = 823.543

2. (-2)⁴ x (-2)⁵ = -2⁴⁺⁵   = -2⁹  = – 512

3. (-3)³ x (-3)⁷ = -33⁺⁷   = -3¹⁰  = 59.049

4. 2³ x  3⁴  , soal ini tidak bisa kita sederhakan kembali sebab bilangan pokonya berbeda (2 dan 3). Sehingga, kita hanya dapat menghitung nilainya saja, yaitu:
2³ x  3⁴  = 8 x 81 = 648

5. 3y² x y³ = 3(y)²⁺³  = 3y⁵

6. 2x⁴ x 3x⁶ = (2 x 3)(x) ⁴⁺⁶ = 6x¹⁰

7. -2² x 2³ = (-1)² x 2² x 2³ = (1) x 2²⁺³ = 2⁵ = 32

Untuk kasus bilangan pokok negatif yang berpangkat, seperti pada nomor 2, 3 , 7 terdapat poin penting yang harus kalian ketahui, yaitu:

2. Sifat Pembagian Bilangan Berpangkat

Pada operasi hitung pembagian bilangan berpangkat, maka akan berlaku sifat seperti di bawah ini:

a^m : aⁿ = a^m-n

5⁶ x 5³ = (5 x 5 x 5 x 5 x 5 x 5) x (5 x 5 x 5)

5⁶ x 5³ = 5 x 5 x 5 (coret (5 x 5 x 5) x (5 x 5 x 5))

5⁶ x 5³ = 5³

Sehingga, bisa kita simpulkan menjadi 5⁶ x 5³ = 5^6-3

Contoh Soal Sifat Pembagian Bilangan Berpangkat dan Pembahasannya

1. 4⁵ / 5³
2. 3⁴ / 2³

1. 4⁵ / 5³ = 4^5-3 = 4² = 16

2. 3⁴ / 2³, soal ini tidak bisa kita sederhakan kembali sebab bilangan pokonya berbeda (3 dan 2). Sehingga, kita hanya dapat menghitung nilainya saja, yaitu:

3⁴ / 2³ = 81/ 8 = 10,125

3. Sifat Perpangkatan Bilangan Berpangkat

Pada operasi hitung perpangkatan bilangan berpangkat, maka akan berlaku sifat seperti berikut ini:

(a^m)ⁿ = a^mxn

Untuk lebih memahami cara mengenai rumus di atas, perhatikan uraian di bawah ini:

(5³)² =(5 x 5 x 5)²

(5³)² = (5 × 5 × 5) × (5 × 5 × 5)

(5³)² = 5⁶

Sehingga, bisa kita simpulkan menjadi (5³)² = 5^3×2

Contoh Soal Sifat Perpangkatan Bilangan Berpangkat beserta Pembahasannya

1. (4³)⁵
2. [(-2)⁴]²

1. (4³)⁵ = 4^3×5 = 4¹⁵ = 1.073.741.824
2. [(-2)⁴]² = (-2)^4×2 = (-2)⁸ = 256

4. Sifat Perpangkatan Suatu Perkalian Dua Bilangan

Pada operasi hitung perpangkatan pada sebuah perkalian dua bilangan, maka akan berlaku sifat seperti berikut ini:

(a x b)^m = a^m x b^m

Untuk lebih memahami cara mengenai rumus di atas, perhatikan uraian di bawah ini:

(3 x 5)² = (3 x 5) x (3 x 5)

(3 x 5)² =(3 x 3) x (5 x 5)

(3 x 5)² = 3² x 5²

Sehingga, bisa kita simpulkan menjadi (3 x 5)² = 3² x 5²

Contoh Soal Sifat Perpangkatan Suatu Perkalian 2 Bilangan dan Pembahasannya

1. (2 x 7)²
2. [(1/2) x (1/3)]³

1. (2 x 7)² = 2² x 7² = 4 x 49 = 196
2. [(1/2) x (1/3)]³ = (1/2)³ x (1/3)³ = (1/8) x (1/27) = 1/216

5. Sifat Perpangkatan Suatu Pembagian Dua Bilangan

Dalam operasi hitung perpangkatan suatu pembagian dua bilangan, berlaku sifat sebagai berikut:

(a : b)^m = a^m : b^m

Untuk lebih memahami cara mengenai rumus di atas, perhatikan uraian di bawah ini:

(3/5)² = (3/5) x (3/5)

(3/5)² = (3 x 3)/(5 x 5)

(3/5)² = 3²/5²

Sehingga, bisa kita simpulkan menjadi (3/5)² = 3²/5²

Contoh Soal Sifat Perpangkatan Suatu Pembagian 2 Bilangan dan Pembahasannya

Sederhanakan hasil perpangkatan dari bilangan berpangkat di bawah ini, lalu tentukan nilainya!

1. (2/3)²
2. [(−3)/2]³

1. (2/3)² = 2²/5² = 4/25
2. [(−3)/2]³ = (−3)³/2³ = −27/8

6. Sifat Perpangkatan Bilangan nol

Apabila a merupakan bilangan real (a ∈ R) serta n merupakan bilangan bulat positif  (n ≥ 1), maka sifat-sifat perpangkatan  bilangan 0 (nol) ialah sebagai berikut:

1. a^o = 1
2. 0ⁿ = 0
3. 0^o = tak terdefinisi

Untuk membuktikan sifat pangkat darir bilangan nol nomor 1, simak penjelasan di bawah ini:

2⁴ : 2⁴ = 2^4-4 = 20 sehingga,

2⁴ : 2⁴ = 2⁰, sebab 2⁴ : 2⁴ = 16/16 = 1, maka

2⁰ = 1

Dengan pembuktian tersebut, maka dapat kita simpulkan jika seluruh bilangan real kecuali nol jika kita pangkatkan dengan 0 (nol) maka hasilnya akan sama dengan 1.

Untuk pembuktian sifat pangkat bilangan nol nomor 2, simak penjelasan di bawah ini:

0¹ = 0 × 0 = 0

0² = 0 × 0 × 0 = 0

0³ = 0 × 0 × 0 × 0 = 0

Dengan pembuktian di atas, maka bisa kita simpulkan jika bilangan nol apabila kita pangkatkan sebanyak apa pun hasilnya akan selalu nol.

Untuk pembuktian sifat pangkat bilangan nol nomor 3, simak penjelasan di bawah ini:

Kita tahu jika nilai 0ⁿ = 0, sehingga,

0ⁿ/0ⁿ = 0/0, nilai 0/0 = seluruh bilangan, karena seluruh bilangan dikalikan nol hasilnya yaitu nol.

Maka dapat kita tuliskan bentuk persamaan lainnya, seperti:

0ⁿ/0ⁿ = 0^n-n

0ⁿ/0ⁿ = 00 karena 0ⁿ/0ⁿ = 0/0 = seluruh bilangan, maka

0⁰ = seluruh bilangan

seluruh bilangan artinya dapat 1, 12, 123, 1234, 12345, 13456 dan seterusnya. Maka dari itu, definisinya tidak jelas.

Sehingga bisa kita simpulkan jika bilangan nol pangkat nol hasilnya tidak terdefinisi.

Bentuk Akar

Bentuk akar merupakan akar dari suatu bilangan-bilangan yang hasilnya bukan termasuk ke dalam bilangan rasional (bilangan yang meliputi bilangan cacah, bilangan prima, serta bilangan-bilangan lain yang terkait) atau bilangan irasional (yakni bilangan yang hasil baginya tidak pernah berhenti).

Bentuk akar adalah bentuk lain untuk menyebutkan suatu bilangan yang berpangkat.

Bentuk akar termasuk ke dalam bilangan irasional di mana bilangan irasional tidak bisa disebutkan dengan menggunakan bilangan pecahan a/b, a serta b bilangan bulat a dan b ≠ 0.

Bilangan dari bentuk akar merupakan suatu bilangan yang ada di dalam tanda √ yang disebut sebagai tanda akar. 

Beberapa contoh bilangan irasional di dalam bentuk akar yakni √2, √6, √7, √11 dan lain sebagainya.

Sementara untuk √25 bukanlah bentuk akar, sebab √25 = 5  (5 merupakan bilangan rasional) sama saja angka 25 bentuk akarnya yaitu √5.

Simbol akar “√” pertama kali diperkenalkan oleh seorang matematikawan asal Jerman yang bernama Christoff Rudoff.

Di dalam bukunya dengan judul Die Coss. Simbol tersebut dipilih sebab mirip dengan huruf ” r ” yang mana diambil dari kata “radix”, yang merupakan bahasa latin bagi akar pangkat dua.

Sebagaimana bilangan berpangkat yang mempunyai beberapa sifat-sifat, bentuk dari akar pun juga mempunyai beberapa sifat, diantaranya yakni:

1. √a² = a
2. √a x b = √a x √b ; a ≥ 0 dan b ≥ 0
3. √a/b = √a/√b ; a ≥ 0 dan b ≥ 0

Demikianlah ulasan singkat kali ini yang dapat kami sampaikan mengenai Bilangan Berpangkat – Eksponen. Semoga ulasan di atas mengenai Bilangan Berpangkat – Eksponen dapat kalian jadikan sebagai bahan belajar kalian.