Diagram menjadi salah satu cara yang dapat dipakai untuk memudahkan kalian untuk melihat suatu data, salah satu jenisnya adalah diagram lingkaran.
Daripada menyajikan data dengan menggunakan susunan angka yang rumit, visualisasi dari diagram tentunya akan lebih mudah untuk dipahami.
Bentuk diagram ini sendiri sudah sangat umum dipakai untuk menunjukan beragam macam data maupun nilai.
Dan kali ini, kita akan mencari tahu lebih lanjut terkait pengertian, rumus hingga cara menghitung diagram lingkaran. Simak baik – baik ya.
Daftar Isi
Pengertian Diagram Lingkaran
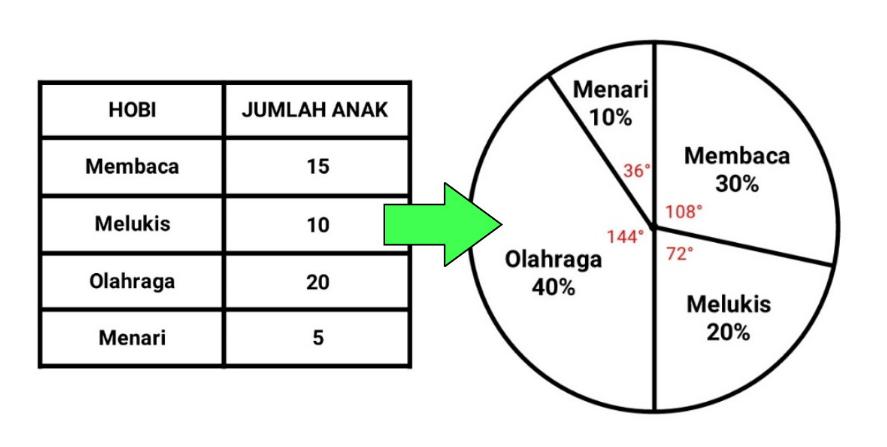
Diagram lingkaran merupakan suatu diagram yang menunjukkan data maupun hasil beragam angka dalam wujud lingkaran.
Bentuk diagram ini biasanya akan membagi data statistik menjadi beberapa sektor atau bagian.
Pada masing – masing sektor pada diagram lingkaran akan mewakili bagian yang proporsional dari keseluruhan data.
Diagram satu ini sangat pas digunakan untuk menjumpai komposisi sesuatu.
Bentuk dari diagram satu ini pun dapat menggantikan grafik lain seperti grafik garis, grafik batang, histogram, plot garis, atau yang lainnya.
Biasanya, diagram lingkaran di dalam soal Matematika kerap kali dimanfaatkan untuk mengetahui perbandingan dari Total Jumlah pada suatu permasalahan.
Atau dengan kata lain, untuk mengetahui Pembesaran Daerah/ Pembatasan Daerah dalam pembahasan suatu data.
Adapun beberapa jenis dari diagram lingkaran yang perlu kalian ketahui, yaitu:
- Diagram lingkaran normal (dalam wujud angka)
- Diagram lingkaran dalam persentase (%)
- Diagram lingkaran dalam derajat (°)
Masing – masing jenis tersebut juga mempunyai cara untuk menghitungnya sendiri. Selengkapnya akan di bahas pada bab di bawah.
Rumus Diagram Lingkaran
Seperti yang telah disebutkan sebelumnya, dalam setiap jenis diagram lingkaran memiliki cara perhitungannya sendiri – sendiri, nah berikut ini adalah beberapa rumusnya, simak baik baik ya!
1. Diagram Lingkaran Normal
Cara menghitung diagram lingkaran normal yang berbentuk angka, kalian bisa menghitungnya sesuai dengan rumus umum yang ada di bawah ini:
Data yang ditanyakan = Total Data – Data Total yang Diketahui
Kalian hanya butuh untuk memasukan informasi atau data sesuai dengan apa saja yang telah diketahui.
2. Diagram Lingkaran dalam Persen
Untuk dapat menghitung nilai persentase dari suatu diagram lingkaran, maka berikut ini adalah rumus yang dapat kalian gunakan, antara lain:
Nilai yang Dibutuhkan = (Persentase Nilai yang Ditanyakan/ 100%) x Nilai Total
atau
Persentase Suatu Sektor = Data yang Diberikan / Nilai Total Data x 100%
Dengan rumus tersebut, kalian dapat mengetahui persentase dari suatu bagian dengan menggunakan diagram lingkaran, atau nilai dari persentase di dalam diagram lingkaran.
3. Diagram Lingkaran dalam Derajat
Cara menghitung nilai dari diagram lingkaran dalam derajat, kalian dapat menggunakan rumus sebagai berikut:
Nilai yang Dibutuhkan = (Nilai Sudut / 360°) x Nilai Total
atau
Sudut Suatu Sektor = Data yang Diberikan / Nilai Total Data x 360°
Kalian dapat menyesuaikan dengan apa yang diketahui di dalam soal/ permasalahan, kemudian kalian pilih di antara kedua rumus tersebut untuk memperoleh data dalam wujud diagram lingkaran sudut.
4. Rumus Teori Perbandingan
Di dalam teori perbandingan satu ini, kalian bisa menggunakan diagram dalam wujud derajat dan juga persen.
Teori perbandingan ini amat bermanfaat untuk menemukan nilai di dalam penelitian ketika sedikit data yang diketahui.
Perhatikan uraian di bawah ini:
Diketahui A dan B.
Keterangan:
Persentase A = nilai A atau derajat A = nilai A
Persentase B = nilai B atau derajat B = nilai B
Dari data yang ada di atas, kalian dapat membandingkan A dengan B seperti dibawah ini:
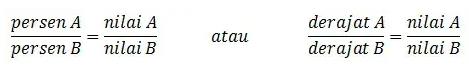
Sedangkan untuk rumusnya adalah sebagai berikut:
a. Rumus untuk Mencari Nilai
Nilai A = (Persentase A/ Persentase B) x Nilai B
atau,
Nilai A = (Derajat A/ Derajat B) x Nilai B
Nilai B = (Persentase B/ Persentase A) x Nilai A
atau,
Nilai B = (Derajat B/ Derajat A) x Nilai A
Sedangkan,
b. Rumus untuk Mencari Persentase atau Derajat
Persentase A = (Nilai A / Nilai B) x Persentase B
atau,
Derajat A = (Nilai A / Nilai B) x Kelas B
Persentase B = (Nilai B / Nilai A) x Persentase A
atau,
Derajat B = (Nilai B / Nilai A) x Catatan A
Penggunaan Diagram Lingkaran
Diagram lingkaran banyak sekali dipakai sebab kemudahan nya dalam kebutuhan membaca datanya. Hal tersebut menjadi wujud paling sederhana sebab data bisa dengan mudah dibandingkan di dalam suatu diagram lingkaran.
Berikut ini adalah beberapa contoh dari penggunaan diagram lingkaran, antara lain:
- Di dalam bisnis, diagram ini dipakai untuk membandingkan kawasan pertumbuhan seperti keuntungan bisnis, eksposur, omset, dan lainnya.
- Di sekolah, diagram lingkaran bisa dimanfaatkan untuk menunjukkan berapa banyak waktu yang dialokasikan pada setiap bagian.
- Diagram ini juga sering dipakai untuk mewakili data kategorikal.
- Jumlah pelanggan di waktu akhir pekan.
- Dipakai untuk mengukur data ukuran relatif seperti tipe rumah, tipe kendaraan roda 2/ roda 4.
- Jenis makanan serta minuman yang disukai oleh orang – orang pada suatu restoran.
- Perbandingan penjualan beragam merek.
- Representasi merek di dalam pasar.
Contoh Soal
Untuk memudahkan kalian dalam memahami uraian di atas, berikut ini kami berikan beberapa contoh soal yang dapat kalian pelajari, antara lain:
1. Contoh Soal Diagram Normal
Suatu kelas mempunyai total 42 siswa di dalam bentuk diagram lingkaran berikut ini:
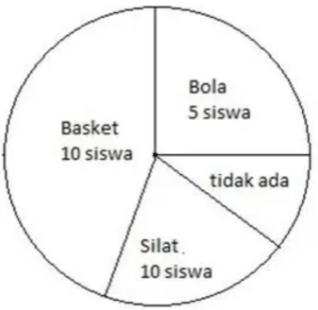
Waktu banyak siswa berpartisipasi di dalam kegiatan ekstrakurikuler, seperti yang telah ditunjukkan dalam gambar diagram lingkaran diatas. Berapa banyak siswa yang tidak mengikuti kegiatan ekstrakurikuler?
Jawab:
Diketahui:
- Total siswa = 42 siswa
- Ekskul bola = 5 siswa
- Ekskul basket = 10 siswa
- Ekskul silat = 10 siswa
Ditanya:
Siswa yang tidak mengikuti ekstrakurikuler?
Penjelasan:
Data yang Ditanyakan = Total Data – Data yang Diketahui Total
Sehingga siswa yang tidak mengikuti yaitu:
= jumlah total siswa – (ekskul bola + ekskul basket + ekskul silat)
= 42 siswa – (5 siswa + 10 siswa + 10 siswa)
= 42 siswa – 25 siswa
= 17 siswa
Dengan demikian, siswa yang tidak mengikuti ekstrakurikuler ada 17 siswa.
2. Contoh Soal Diagram Derajat
Suatu sekolah mempunyai 1.260 siswa. Di dalam sekolah ini, siswa harus hadir dalam kegiatan ekstrakurikuler.
Pada saat siswa mengambil program ekstrakurikuler, digambarkan dalam bentuk diagram lingkaran derajat (°) seperti berikut ini:
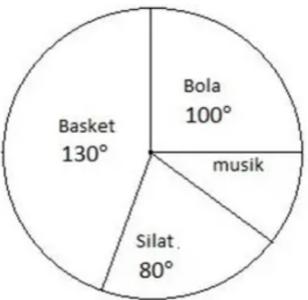
Tentukan berapa siswa yang mengikuti ekskul musik?
Jawab:
Diketahui:
- Total siswa = 1260 siswa
- Ekskul bola = 100°
- Ekskul basket = 130°
- Ekskul silat = 80°
Ditanya:
Banyak siswa yang memilih mengikuti ekskul musik ekstrakurikuler?
Dijawab:
Pertama, kalian dapat mencari tahu berapa banyak siswa yang mengikuti musik ekstrakurikuler, yaitu:
Ekskul musik = 360 ° – (ekskul basket + ekskul bola + ekskul silat)
= 360° – (130° – 100° – 80°)
= 360° – 310°
= 50°
Lalu kalian pakai rumus untuk menentukan jumlah siswa yang belajar musik:
Jumlah siswa yang mengikuti ekskul musik = (musik/ 360°) x jumlah total siswa
= (50°/360°) x 1260 siswa
= 63000/360
= 175 siswa
Sehingga diketahui terdapat 175 siswa yang mengikuti musik ekstrakurikuler.
3. Soal Diagram dalam Persentase
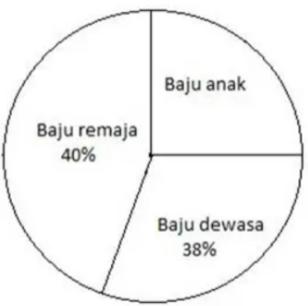
Diketahui dari data yang ada di atas, jika total barang dagangan yang dijual oleh pedagang ada sebanyak 300.
Lantas berapa banyak item pakaian untuk anak -anak yang dijual?
Jawab:
Diketahui:
- Total pakaian = 300 bagian
- Pakaian dewasa = 38%
- Pakaian remaja = 40%
Ditanya:
Tentukan banyak baju anak yang dijual!
Penjelasan:
Pertama, kalian dapat melihat persentase pakaian anak – anak yang dijual.
Persentase pakaian anak = 100% – (pakaian remaja + pakaian dewasa)
= 100% – (40% + 38%)
= 100% – 78%
= 22%
Sehingga kalian dapat memakai persentase pakaian anak yang kalian peroleh dengan rumus yang ada di atas.
Jumlah pakaian anak = (persentase anak/ 100%) x pakaian keseluruhan
= (22%/ 100%) × 300 buah
= 6600/100
= 66 buah
Sehingga diketahui jumlah pakaian anak – anak yang dijual oleh pedagang ada sebanyak 66 buah.
4. Soal Teori Perbandingan
Suatu sekolah mempunyai data terkait siswa yang mengerjakan kegiatan di luar sekolah dalam wujud diagram berikut ini:
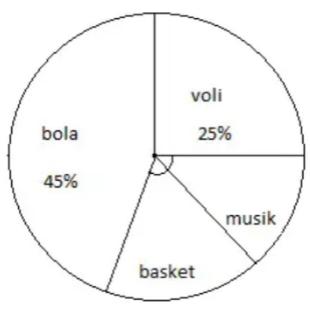
Jika terdapat 450 siswa yang mengambil bola, maka tentukan banyak siswa yang bermain bola voli!
Jawab:
Diketahui:
- Persen bola ekstrakurikuler = 45%
- Jumlah bola = 450 siswa
- Persen bola voli = 25%
Ditanya:
Jumlah siswa yang bermain bola voli.
Penjelasan:
Bola voli = (persentase bola voli/ persentase bola voli) x jumlah ekskul bola
= (25% / 45%) × 450
= 11250/45
= 250 siswa
Maka diketahui ada 250 siswa yang bermain bola voli.
5. Soal Diagram dalam Persentase
Statistik jumlah mahasiswa dibagi ke dalam empat kategori jurusan universitas, antara lain:
- 420 jurusan sains
- 410 jurusan seni
- 540 jurusan teknik.
- 900 jurusan bahasa
Berapakah persentase dari masing – masing jurusan?
Penjelasan:
Tambahkan seluruh angka untuk memperoleh total, seperti berikut ini:
410 + 420 + 900 + 540 = 2270410 + 420 + 900 + 540 = 2270
Kemudian kalian bagi ke setiap kategori dengan totalnya. Hasilnya seperti:
Seni: 410 ÷ 2270 = 0,18
Sains: 420 ÷ 2270 = 0,18
Bahasa: 900 ÷ 2270 = 0,40
Teknik: 540 ÷ 2270 = 0,24
Langkah selanjutnya adalah masing – masing desimal dengan 100 untuk memperoleh persentase, sehingga hasilnya yaitu:
Seni: 18 persen
Sains: 18 persen
Bahasa: 40 persen
Teknik: 24 persen.