Ketika dihadapkan dengan data yang sangat banyak, untuk membantu mengatur data itu sering kali memanfaatkan tabel, pada Daftar Frekuensi atau Sebaran Frekuensi (Distribusi Frekuensi) ini juga menggunakan tabel dalam penerapannya. Berikut informasi selengkapnya.
Daftar Isi
Pengertian Distribusi Frekuensi

1. Secara Umum
Kata distribusi berasal dari bahasa inggris “distribution” yang artinya pembagian, penyaluran, atau pancaran. Semnetara frekuensi juga berasal dari bahasa Inggris “frequency” yang artinya keseringan, kekerapan, atau jarang-kerapnya. Di dalam ilmu statistika, frekuensi diartikan sebagai seberapa kali sebuah variabel yang dilambangkan dengan angka (bilangan) berulang kali di dalam deretan data angka tersebut.
Sehingga dapat kita ketahui bahwa distribusi frekuensi adalah sebuah kondisi yang menggambarkan bagaimana frekuensi dari variabel atau gejala yang dilambangkan dengan angka tersebut sudah terbagi, tersalur, tersebar, serta terpancar.
Penggambaran bilangan atau angka atau penyajian data angka itu bisa disajikan pada bentuk tabel maupun grafik / gambar, yang lalu dikenal dengan istilah tabel distribusi frekuensi serta grafik distribusi frekuensi.
2. Menurut Para Ahli
Berikut pengertian distribusi frekuensi menurut para ahli, antara lain:
a. Riduwan (2003)
Merupakan penyusunan sebuah data mulai dari yang terkecil hingga terbesar dengan membagi banyaknya data ke dalam beberapa kelas. Fungsi dari data yang masuk di dalam distribusi frekuensi yakni guna memudahkan data untuk penyajian, mudah dipahami, serta mudah dibaca sebagai informasi. Selain itu, data ini juga dipakai untuk perhitungan pada gambar statistik.
b. Hasan (2009)
Merupakan suatu susunan data menurut kelas – kelas interval tertentu atau menurut kelompok tertentu pada suatu daftar.
Bagian – Bagian Distribusi Frekuensi

Menurut pernyataan dari Hasan (2009), adapun beberapa bagian dari distribusi frekuensi, diantaranya yaitu:
1. Kelas – Kelas
Kelas merupakan kelompok nilai data.
2. Batas Kelas
Batas kelas merupakan berbagai nilai yang membatasi kelas antara satu kelas dengan kelas yang lainnya.
Terdapat dua batas kelas, antara lain:
- Batas bawah kelas ada pada sebelah kiri deretan kelas.
- Batas atas kelas ada pada sebelah kanan deretan kelas.
3. Tepi Kelas
Tepi kelas merupakan batas kelas yang tidak mempunyai lubang atau wadah untuk angka tertentu antara kelas yang satu dengan kelas yang lainnya.
Tepi kelas satu ini berfungsi pada saat pembuatan histogram.
Apabila pada ujung atas interval kelas pertama ditambah dengan ujung bawah interval kedua serta kemudian dikalikan setengah, maka hasil itu disebut sebagai tepi kelas.
Atau pada saat ujung bawah interval kelas dikurangi dengan 0,5 atau 0,05 bahkan 0,005 tergantung ketelitian data yang dibuat oleh si peneliti serta pada ujung kelas atas ditambah dengan 0,5 atau 0,05 atau 0,005 maka nilai tersebut disebut sebagai batas kelas.
4. Titik Tengah Kelas
Adalah nilai data yang berada ditengah – tengah kelas.
Titik tengah kelas = ½(batas atas kelas + batas bawah kelas)
5. Interval
Adalah selang yang memisahkan antara kelas yang satu dengan kelas yang lainnya.
6. Panjang interval kelas
Merupakan jarak antara tepi atas kelas dengan tepi bawah kelas.
7. Frekuensi Kelas
Merupakan banyaknya data yang masuk ke dalam kelas tertentu.
Contoh:
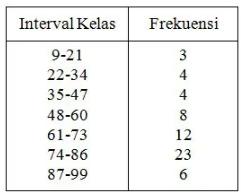
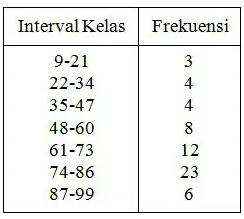
Dari distribusi frekuensi diatas :
- Banyaknya kelas yakni 7.
- Batas kelas – kelas yaitu 9, 21, 22, 34, …
- Batas bawah kelas – kelas yaitu 9, 22, 35, 48, 61, 74, 87
- Batas atas kelas – kelas yaitu 21, 34, 47, 60, 73, 86, 99
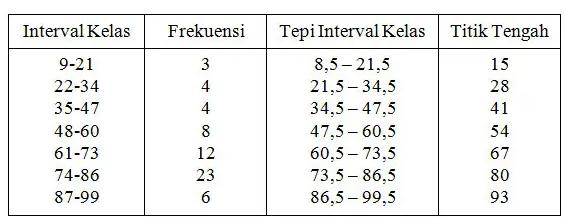
- Tepi bawah kelas yaitu 8,5; 21,5; 34,5; 47,5; 60,5; 73,5; 86,5
- Tepi atas kelas yaitu 21,5; 34,5; 47,5; 60,5; 73,5; 86,5; 99,5
- Titik tengah kelas yaitu 15, 28, 41, 54, 67, 80, 93
- Interval kelas yaitu 9-21, 22-34, 35-47, 48-60, 61-73, 74-86, 87-99.
- Panjang interval kelas – kelas masing – masing yaitu 13.
- Frekuensi kelas – kelas yaitu 3, 4 ,4 ,8 ,12 ,23 ,6.
Histogram, Poligon dan Ogive
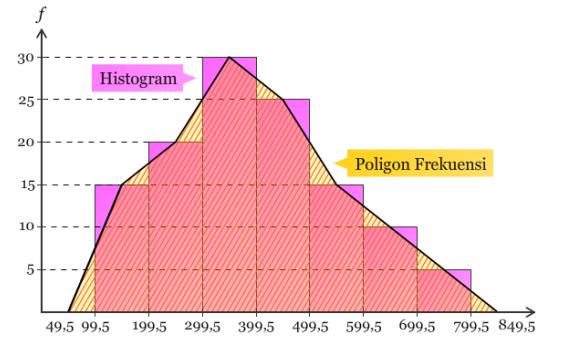
1. Histogram dan Poligon Frekuensi
Poligon dan histogram frekuensi menjadi dua grafik yang kerap dipakai untuk menggambarkan distribusi frekuensi.
Histogram merupakan grafik batang dari distribusi frekuensi, sedangkan poligon frekuensi adalah grafik garisnya.
Di dalam histogram, batang – batangnya saling melekat / berhimpitan. Sementara pada poligon frekuensi dibuat dengan cara menarik garis dari sebuah titik tengah batang histogram menuju titik tengah batang histogram yang lain.
Supaya didapatkan poligon tertutup, maka harus dibuat dengan dua kelas baru dengan panjang kelas uang sama dengan frekuensi nol terhadap kedua ujungnya.
Pembuatan dua kelas baru tersebut diperkenankan sebab luas histogram & poligon yang tertutup sama.
Dalam pembuatan histogram menerapkan sistem salib sumbu, yakni:
Sumbu mendatar (sumbu X) menyatakan interval kelas (tepi bawah serta tepi atas tiap – tiap kelas) dan juga sumbu tegak (sumbu Y) yang menyatakan frekuensi.
Contoh:
Data Hasil Ujian Akhir Mata Kuliah Statistika dari 60 Orang Mahasiswa
2. Kurva Frekuensi / Ogive / Ogif
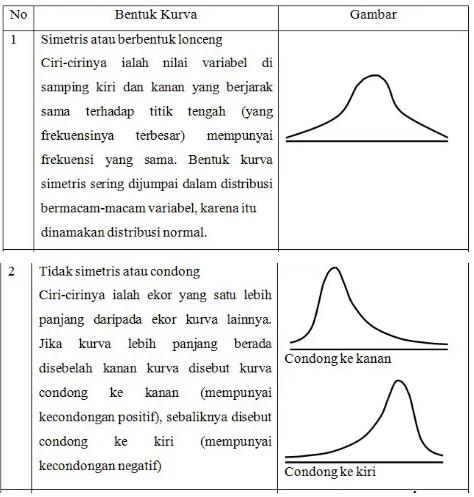
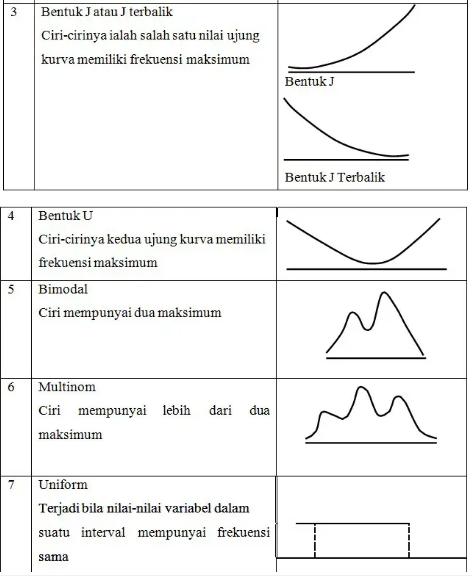
Kurva distribusi frekuensi atau kurva frekuensi yang sudah dihaluskan memiliki beberapa bentuk dengan ciri – ciri tertentu.
Berikut adalah beberapa bentuk kurva distribusi frekuensi, antara lain:
Jenis – Jenis Distribusi Frekuensi
Berdasarkan kriterianya, distribusi frekuensi terbagi ke dalam tiga jenis yang berbeda, diantaranya yaitu:
1. Distribusi Frekuensi Biasa
Distribusi frekuensi biasa isinya berupa jumlah frekuensi dari masing – masing kelompok data.
Jenis ini juga dibagi menjadi dua bagian yang berbeda, yaitu:
a. Distribusi Frekuensi Numerik
Merupakan distribusi frekuensi dimana pembagian kelasnya dinyatakan dengan menggunakan angka.
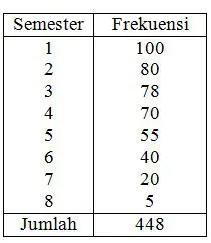
b. Distribusi Frekuensi Peristiwa
Merupakan distribusi dimana pada pembagian kelasnya dinyatakan berdasarkan golongan data yang ada.
Mahasiswa Pendidikan Matematika
2. Distribusi Frekuensi Relatif
Distribusi relatif ini isinya berupa nilai – nilai hasil bagi antara frekuensi kelas dengan jumlah pengamatan.
Jenis ini menyatakan proporsi data yang ada dalam sebuah kelas interval.
Distribusi frekuensi relatif di dalam sebuah kelas diperoleh dengan cara membagi frekuensi dengan total data yang terdapat pada pengamatan / observasi, berikut rumusnya:
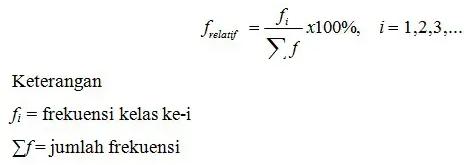
Frekuensi relatif terkadang dinyatakan pada bentuk perbandingan, desimal, maupun persen.
Contoh:
Nilai Ujian Akhir Mata Kuliah Statistika
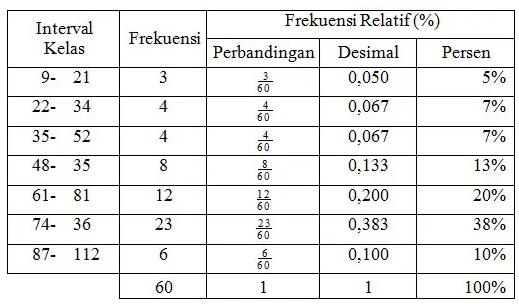
3. Distribusi Frekuensi Kumulatif
Distribusi frekuensi kumulatif merupakan distribusi frekuensi yang isinya berupa frekuensi kumulatif atau frekuensi yang dijumlah.
Jenis ini mempunyai grafik / kurva yang disebut dengan OGIF.
Di dalam ogif nantinya akan dicantumkan frekuensi kumulatifnya serta memakai nilai batas kelas.
Terdapat dua macam pada distribusi frekuensi kumulatif, antara lain:
a. Distribusi Frekuensi Kumulatif Kurang Dari
Distribusi frekuensi kumulatif kurang dari merupakan distribusi frekuensi yang isinya memuat jumlah frekuensi dengan nilai kurang dari nilai batas kelas sebuah interval tertentu.
Contoh:
Nilai Ujian Akhir Mata Kuliah Statistika
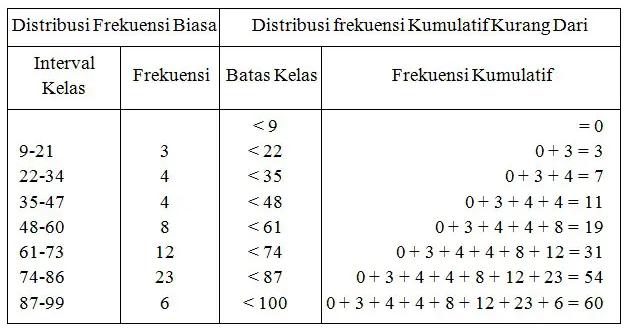
Ogif frekuensi kumulatif kurang dari data di atas:
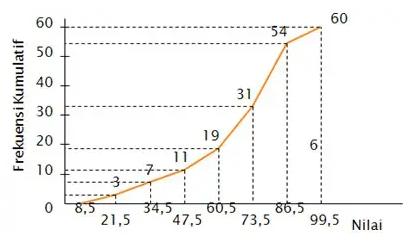
b. Distribusi Frekuensi Kumulatif Lebih Dari
Distribusi frekuensi kumulatif lebih dari merupakan distribusi frekuensi yang isinya berupa jumlah frekuensi yang mempunyai nilai lebih dari nilai batas kelas sebuah interval tertentu.
Contoh:
Nilai Ujian Akhir Mata Kuliah Statistika
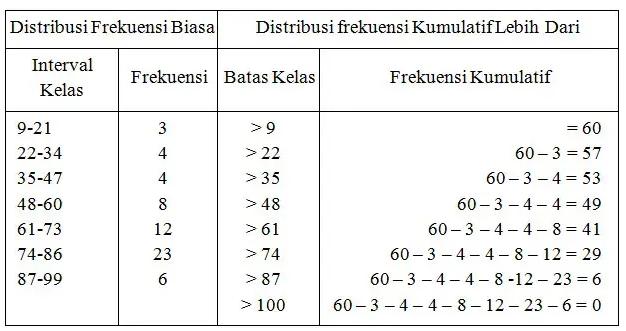
Ogif frekuensi kumulatif lebih dari data di atas:
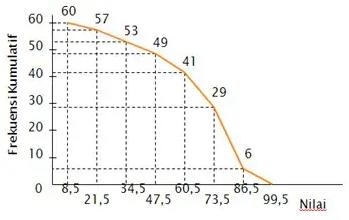
Cara Membuat Distribusi Frekuensi
Berikut langkah mudah untuk membuat distribusi frekuensi, antara lain:
- Mengurutkan data dari yang terkecil menuju yang paling besar.
- Menentukan jangkauan atau range data (R)
Jangkauan = data terbesar – data terkecil - Menentukan banyak kelas (k) dengan memakai Rumus Sturgess:
k=1+3,3 log n - Menentukan panjang interval kelas (i) dengan rumus:
i = Jangkauan / banyak kelas - Batas bawah kelas pertama
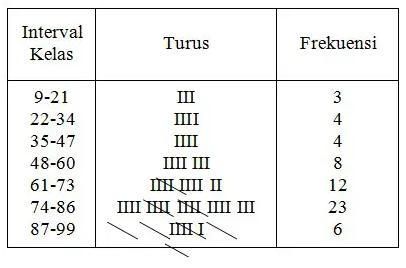
Batas bawah kelas pertama pada umumnya dipilih dari data yang paling kecil dan biasanya berasal dari pelebaran jangkauan (data yang lebih kecil dari data terkecil) serta selisihnya harus kurang dari panjang interval kelasnya. - Mencatat frekuensi kelas secara melidi pada kolom turus / tally (sistem turus) sesuai dengan banyaknya data. Contoh:
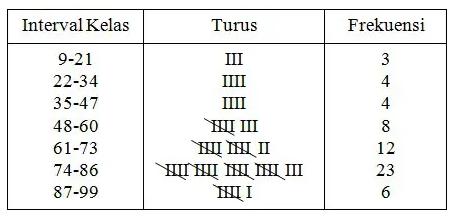
- Lalu langkah terakhir membuat tabel distribusi frekuensi dengan cara memindahkan seluruh angka frekuensi (f)
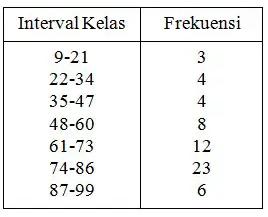
Contoh Soal
Berikut adalah contoh soal untuk membuat tabel distribusi frekuensi:
1. Diketahui data hasil ujian akhir untuk mata kuliah statistika dari 60 orang mahasiswa:
23 60 79 32 57 74 52 70 82 36
80 77 81 95 41 65 92 85 55 76
52 10 64 75 78 25 80 98 81 67
41 71 83 54 64 72 88 62 74 43
60 78 89 76 84 48 84 90 15 79
34 67 17 82 69 74 63 80 85 61
Buatlah daftar distribusi frekuensi dari data yang ada di atas!
Jawab:
a. Mengurutkan data:
10 32 43 55 62 67 72 76 79 81 84 89
15 34 48 57 63 67 74 76 79 81 84 90
17 36 52 60 64 69 74 77 80 82 85 92
23 41 52 60 64 70 74 78 80 82 85 95
25 41 54 61 65 71 75 78 80 83 88 98
b. Jangkauan (R) = 98 – 10 = 88
c. Banyak kelas (k) = 1 + 3,3 log 60 = 6,8 ≈ 7
d. Lebar interval kelas (i) = 88 / 7 = 12,5 ≈ 13
e. Batas kelas pertama, contohnya kita ambil 9
f. Menuliskan frekuensi secara melidi atau turus
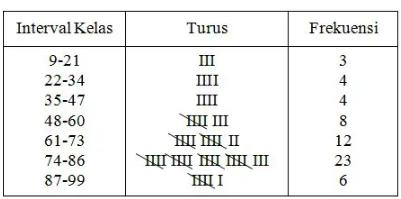
g. Membuat tabel distribusi frekuensi dengan cara memindahkan seluruh angka frekuensi (f)