HUKUM KIRCHHOFF 1 & 2: Penemu, Rumus, Contoh Soal

Kirchhoff adalah salah satu fisikawan yang memberi jasa dalam ilmu kelistrikan. Beliau terkenal dengan Hukum Kirchhoff I dan II. Ditemukan oleh seorang yang bernama lengkap Gustav Robert Kirchhoff, ahli fisika asal Jerman.

Hukum ini menjadi salah satu hukum dalam ilmu elektronika yang memiliki fungsi untuk menganalisis arus serta tegangan pada rangkaian. Dikenalkan oleh Kirchhoff pertama kali pada tahun 1845, terdiri dari dua hukum.

Gustav Robert Kirchhoff

Nama lengkapnya adalah Gustav Robert Kirchhoff, adalah sosok fisikawan dari Jerman yang lahir pada tanggal 12 Maret 1824 di Konigsberg, Prussia. Beliau wafat pada tanggal 17 Oktober 1887, di usia 63 tahun, di Berlin, Jerman.

Ibu Kirchhoff bernama Johanna Henriette Wittke, sedangkan ayahnya adalah Friedrich Kirchhoff yang adalah seorang pengacara. Kirchhoff menikah dengan Clara Richelot pada tahun 1847, mempunyai tiga orang putra dan dua putri.

Setelah Richelot meninggal dunia di 1869, Kirchhoff menikah lagi dengan Luise Brommel di tahun 1872. Menghabiskan sebagian hidupnya sebagai seorang guru besar dan profesor fisika, Kirchhoff memberi kontribusi dengan rumus hukum rangkaian untuk rekayasa listrik pada tahun 1845.

Selain itu, Kirchhoff juga berkontribusi dalam menemukan hukum radiasi termal atau kerap dikenal dengan termodinamika (1859-1861), serta spektroskopi. Di samping itu, tentu saja Hukum Kirchhoff adalah salah satu kontribusi dari beliau juga.

Baca: Konfigurasi Elektron

Hukum Kirchhoff 1

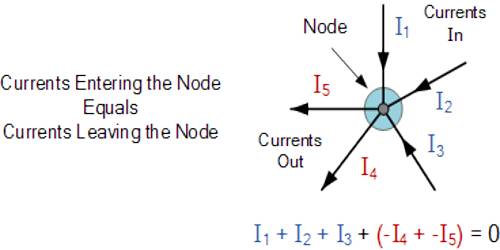
Hukum ini diketahui sebagai junction rule atau hukum percabangan, di mana hukumnya memenuhi kekekalan muatan; dibutuhkan rangkaian multisimpal yang mengandung titik-titik percabangan saat arus terbagi.

Ketika keadaan konstan, tidak ada akumulasi muatan listrik di setiap titik pada rangkaian, sehingga jumlah muatan yang masuk pada setiap titik akan meninggalkan titik itu lagi dengan jumlah yang sama. Bagaimana bunyi Hukum I Kirchhoff?

“Besar arus listrik yang mengalir memasuki suatu titik ke suatu persimpangan atau simpul sama dengan besar arus listrik yang keluar dari titik tersebut.”

Sederhananya, hukum ini berbicara mengenai arus yang ada pada percabangan si suatu rangkaian tertutup. Dasar hukum ini ialah Hukum Kekekalan Muatan dengan bunyi “Muatan di suatu titik A sama dengan muatan yang ada di titik B”, dengan tidak adanya gaya luar yang bekerja.

Rumus Hukum Kirchhoff 1

Secara matematis, Hukum I Kircchoff dinyatakan sebagai berikut.

∑ I_masuk = ∑ I_keluar

Hukum Kirchhoff 2

Hukum ini juga dikenal dengan istilah loop rule atau hukum simpal, sebab aslinya beda potensial pada dua titik percabangan pada satu rangkaian adalah konstan. Hukum ini juga membuktikan adanya Hukum Konservasi Energi.

Apabila muatan Q di sembarang titik dengan potensial V, maka energi dari muatan tersebut adalah QV. Berikutnya, apabila muatan bergerak melintasi simpal, muatan yang ada akan memperoleh tambahan atau malah kehilangan energi ketika melewati resistor baterai atau elemen lain.

Tetapi, ketika kembali ke titik awal kembali, energi muatan tersebut kembali lagi menjadi QV. Bunyi Hukum Kirchhoff 2 adalah sebagai berikut.

“Jumlah keseluruhan voltase pada sekitar loop tertutup di dalam rangkaian memiliki besar yang sama dengan nol.”

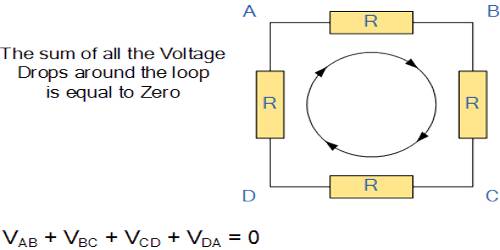
Hukum II Kirchhoff sendiri bertujuan untuk mengukur beda potensial tegangan yang ada pada sebuah rangkaian yang tidak memiliki cabang.

Baca: Rangkaian Listrik

Rumus Hukum Kirchhoff 2

Secara matematis, Hukum II Kirchhoff dinyatakan sebagai berikut.

∑ɛ + ∑IR = 0

Di samping rumus, terdapat sejumlah aturan yang mesti kamu perhatikan dari hukum ini. Tentukan dahulu arah loop pada rangkaian, kemudian terapkan poin-poin berikut.

• Penurunan tegangan (SIR) akan bertanda positif (+) jika searah dengan loop.
• Penurunan tegangan (SIR) akan bertanda negatif (-) jika berlawanan arah dengan loop.

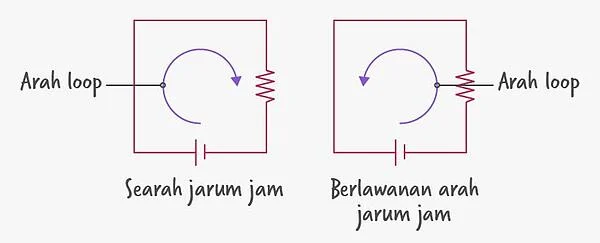
• Gaya Gerak Listrik (SE) akan bertanda positif (+) jika bertemu dengan kutub positif sumber tegangan.
• Gaya Gerak Listrik (SE) akan bertanda negatif (-) jika bertemu dengan kutub negatif sumber tegangan.

Baca: Ikatan Ion

Contoh Soal Hukum Kirchhoff

Supaya kamu lebih paham bagaimana penerapan Hukum I dan II Kirchhoff dalam beberapa model soal, kamu dapat berlatih dan coba menjawab serta memahami pembahasan dari contoh-contoh soal berikut ini.

1. Contoh Soal 1

Diketahui, sebuah rangkaian memiliki kuat arus sebagai berikut. Tentukan bentuk matematis yang tepat dari rangkaian tersebut!

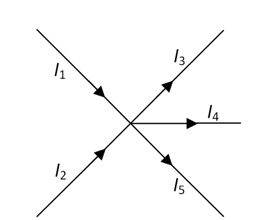
Penyelesaian:

2. Contoh Soal 2

Diketahui, sebuah rangkaian berikut, memiliki arus listrik 3 A, mengalir dari X ke Y dengan beda potensial antara X dan Y adalah 12. Berapa hambatannya?

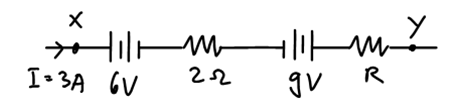
Penyelesaian:

3. Contoh Soal 3

Terdapat rangkaian listrik seperti berikut ini. Dengan Hukum II Kirchhoff, berapa besar kuat arus listrik dalam rangkaian tersebut?

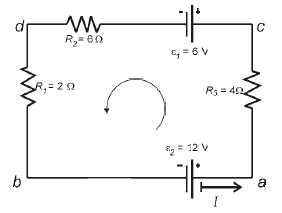
Penyelesaian:

4. Contoh Soal 4

Perhatikan gambar rangkaian listrik berikut ini. Apabila diketahui ɛ₁ = 16 V; ɛ₂ = 8 V; ɛ₃ = 10 V; R₁ = 12 ohm; R₂ = 6 ohm; dan R₃ = 6 ohm, berapa besar kuat arus listrik I?

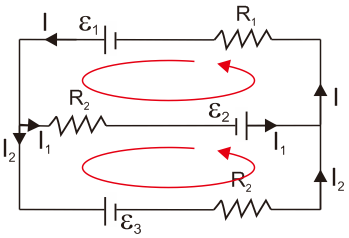
Penyelesaian:

Apakah kamu sudah memahami semua pemaparan Hukum Kirchhoff di atas? Terutama untuk hukum ke dua, jangan sampai salah menentukan arah loop agar jawaban yang dihasilkan pun tidak salah. Selamat berlatih lagi dengan soal-soal dari berbagai sumber!