Integral

Integral tak tentu atau yang dalam bahasa Inggris biasa disebut sebagai Indefinite Integral maupun ada juga yang menyebutnya sebagai Antiderivatif merupakan sebuah bentuk operasi pengintegralan pada suatu fungsi yang menghasilkan suatu fungsi baru.

Fungsi ini belum mempunyai nilai pasti sampai cara pengintegralan yang menghasilkan fungsi tidak tentu ini disebut sebagai integral tak tentu. Selengkapnya mengenai integral tak tentu, simak pembahasan berikut ini.

Integral merupakan suatu konsep penjumlahan secara berkesinambungan dalam matematika. Serta bersama dengan inversnya, diferensiasi, merupakan satu dari dua operasi utama dalam kalkulus.

Integral dikembangkan menyusul dikembangkannya masalah dalam diferensiasi yang mana matematikawan harus berpikir bagaimana menyelesaikan masalah yang berkebalikan dengan solusi diferensiasi. –sc: wikipedia

Pengertian

Pengertian Integral

Integral adalah suatu bentuk pada operasi matematika yang menjadi kebalikan atau biasa juga disebut sebagai invers dari operasi turunan. Serta limit dari jumlah maupun suatu luas daerah tertentu.

Berdasarkan pengertian di atas, terdapat dua macam hal yang harus dilaksanakan di dalam operasi integral yang mana keduanya telah dikategorikan menjadi 2 jenis integral.

Antara lain: integral sebagai invers atau kebalikan dari turunan atau yang biasa juga disebut sebagai Integral Tak Tentu.

Serta yang kedua, integral sebagai limit dari jumlah maupun suatu luas daerah tertentu yang disebut sebagai integral tentu.

Pengertian Integral Tak Tentu

Seperti yang telah disebutkan sebelumya, Integral tak tentu atau yang dalam bahasa Inggris biasa disebut sebagai Indefinite Integral maupun ada juga yang menyebutnya sebagai Antiderivatif merupakan sebuah bentuk operasi pengintegralan pada suatu fungsi yang menghasilkan suatu fungsi baru.

Fungsi ini belum mempunyai nilai pasti sampai cara pengintegralan yang menghasilkan fungsi tidak tentu ini disebut sebagai integral tak tentu.

Apabila f berwujud integral tak tentu dari sebuah fungsi F maka F’= f.

Proses memecahkan antiderivatif adalah antidiferensiasi Antiderivatif yang berhubungan dengan integral lewat “Teorema dasar kalkulus”. Serta memberi cara mudah untuk menghitung integral dari berbagai fungsi.

Integral Tak Tentu

Seperti yang telah dijelaskan sebelumnya, integral tak tentu dalam matematika merupakan invers/kebalikan dari turunan.

Turunan dari sebuah fungsi, apabila diintegralkan akan menghasilkan fungsi itu sendiri.

Mari perthatikan baik-baik contoh dari beberapa turunan dalam fungsi aljabar di bawah ini:

• Turunan dari fungsi aljabar y = x³ adalah y^I = 3x²
• Turunan dari fungsi aljabar y = x³ + 8 adalah y^I = 3x²
• Turunan dari fungsi aljabar y = x³ + 17 adalah y^I = 3x²
• Turunan dari fungsi aljabar y = x³ – 6 adalah y^I = 3x²

Seperti yang telah kita pelajari pada materi turunan, variabel dalam sebuah fungsi akan mengalami penurunan pangkat.

Berdasarkan contoh di atas, maka dapat kita ketahui jika terdapat banyak fungsi yang mempunyai hasil turunan yang sama yakni y^I = 3x².

Fungsi dari variabel x³ maupun fungsi dari variabel x³ yang dikurang atau ditambah pada sebuah bilangan (contohnya: +8, +17, atau -6) mempunyai turunan yang sama.

Apabila turunan itu kita integralkan, maka harusnya akan menjadi fungsi-fungsi awal sebelum diturunkan.

Tetapi, dalam kasus yang tidak diketahui fungsi awal dari sebuah turunan, maka hasil integral dari turunan tersebut bisa kita tulis menjadi:

f(x) = y = x³ + C

Dengan nilai C dapat berapa pun. Notasi C ini juga disebut sebagai konstanta integral. Integral tak tentu dari sebuah fungsi dinotasikan seperti berikut:

Dalam notasi di atas dapat kita baca integral terhadap x”. notasi  disebut integran. Secara umum integral dari fungsi f(x) merupakan penjumlahan F(x) dengan C atau:

Sebab integral dan juga turunan saling berkaitan, maka rumus integral bisa didapatkan dari rumusan penurunan. Apabila turunan:

Maka rumus integral aljabar didapatkan:

dengan syarat apabila n ≠ 1

Sebagai contoh perhatikan beberapa integral aljabar fungsi-fungsi berikut ini:

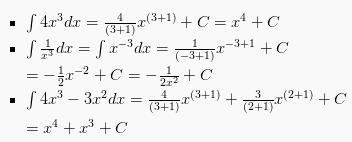
Cara Membaca Integral Tak Tentu

Setelah membaca uraian di atas, taukah kalian cara membaca kalimat integral? Integral di baca seperti ini:

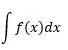yang di baca Integral Tak Tentu Dari Fungsi f(x) Terhadap Variabel X.

Rumus Umum Integral

Berikut ini adalah rumus umum yang ada pada integral:

Pengembangan Rumus Integral

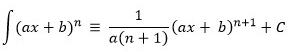
Mari perthatikan baik-baik contoh dari beberapa turunan dalam fungsi aljabar di bawah ini:

• Turunan dari fungsi aljabar y = x³ adalah y^I = 3x²
• Turunan dari fungsi aljabar y = x³ + 8 adalah y^I = 3x²
• Turunan dari fungsi aljabar y = x³ + 17 adalah y^I = 3x²
• Turunan dari fungsi aljabar y = x³ – 6 adalah y^I = 3x²

Uraian mengenai contoh turunan dalam fungsi aljabar di atas silahkan liat lagi pada sub sebelumnya yang ada di atas.

Contoh Soal Integral

Soal 1.

Diketahui:

∫ 8x³ – 3x² + x + 5 dx

Jawab:

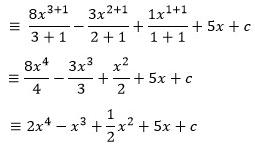
Soal 2.

Diketahui:

∫ (2x + 1) (x – 5) dx

Jawab:

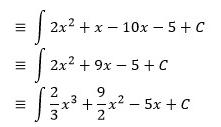
Soal 3.

Diketahui:

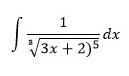
Berapakan integralnya?

Jawab:

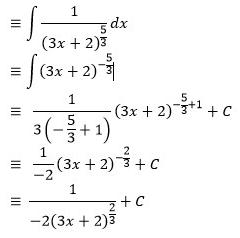
Integral Trigonometri

Integral juga dapat dioperasikan pada fungsi trigonometri.

Pengoperasian integral trigonometri juga dilakukan dengan menggunakan konsep yang sama pada integral aljabar yakni kebalikan dari penurunan. Sehingga bisa kita simpulkan bahwa:

No.	Fungsi f(x) = y	Turunan	Integral
1	y = sin x	cos x	∫ cos xdx = sin x
2	y = cos x	– sin x	∫ sin xdx = – cos x
3	y = tan x	sec2 x	∫ sec2 xdx = tan x
4	y = cot x	– csc2 x	∫ csc2 xdx   = – cot x
5	y = sec x	tan x . sec x	∫ tan x . sec xd = sec x
6	y = csc x	-.cot x . csc x	∫ cot x . csc xdx = – csc x

Selain rumus dasar diatas, ada rumus lain yang bisa digunakan pada pengoperasian integral trigonometri yaitu:

Fungsi f(x) = y	Turunan	Integral
	cos (ax + b)	∫ =  sin (ax + b) + C
	sin (ax + b)	∫ =  cos (ax + b) + C
y =  tan (ax + b)	sec2 (ax + b)	∫=  tan (ax + b) + C
y =  cot (ax + b)	csc2 (ax + b)	∫ =  cot (ax + b)
y =  sec (ax + b)	tan (ax + b) . sec (ax + b)	∫ (ax+b) . sec(ax + b) dx=  sec (ax + b) + C
y =  csc (ax + b)	cot (ax + b) . csc (ax + b)	∫ cot (ax + b) . csc (ax + b) dx =  csc (ax + b)

Sifat Integral

Sifat-sifat dari integral antara lain:

• ∫ k . f(x)dx = k. ∫ f(x)dx                         (dengan k adalah konstanta)
• ∫ f(x) + g(x)dx = ∫ (x)dx + ∫ g(x)dx
• ∫ f(x) – g(x)dx = ∫ f(x)dx – ∫ g(x)dx

Menentukan Persamaan Kurva

Gradien serta persamaan garis singgung kurva pada suatu titik.

Apabila y = f(x), gradien garis singgung kurva pada sembarang titik pada kurva adalah y’ = = f'(x).

Oleh karena itu, apabila gradien garis singgungnya telah diketahui sehingga persamaan kurvanya dapat ditentukan dengan cara seperti berikut ini:

y = ∫ f ‘ (x) dx = f(x) + c

Jika salah satu titik yang melewati kurva telah diketahui, nilai c dapat juga diketahui sehingga persamaan kurvanya dapat ditentukan.

Contoh 1

Diketahui turunan y = f(x) adalah = f ‘(x) = 2x + 3

Jika kurva y = f(x) lewat titik (1, 6), maka tentukan persamaan kurva tersebut.

Jawab:

f ‘(x) = 2x + 3.
y = f(x) = ʃ (2x + 3) dx = x2 + 3x + c.

Kurva melalui titik (1, 6), berarti f(1) = 6 hingga dapat di tentukan nilai c, yakni 1 + 3 + c = 6 ↔ c = 2.

Maka, persamaan kurva yang dimaksud yaitu:

y = f(x) = x2 + 3x + 2.

Contoh 2

Gradien garis singgung kurva pada titik (x, y) ialah 2x – 7. Apabila kurva itu melewati titik (4, –2), maka tentukanlah persamaan kurvanya.

Jawab:

f ‘(x) = = 2x – 7
y = f(x) = ʃ (2x – 7) dx = x2 – 7x + c.

Sebab kurva melewati titik (4, –2)
maka:

f(4) = –2 ↔ 42 – 7(4) + c = –2
–12 + c = –2
c = 10

Maka, persamaan kurva tersebut yakni:

y = x2 – 7x + 10.

Demikianlah ulasan singkat mengenai Turunan Fungsi Aljabar yang dapat kami sampaikan. Semoga ulasan di atas dapat kalian jadikan sebagai bahan belajar kalian.