Jaring – jaring merupakan suatu bentuk asli dari sebuah bangun ruang yang sudah dilakukan pembelahan atau dengan kata lain bangun datar yang jika dikaitkan dapat membentuk suatu bangun ruang, dan kali ini kita akan membahas secara tuntas terkait jarin – jaring balok.
Daftar Isi
Pengertian Jaring – Jaring Balok
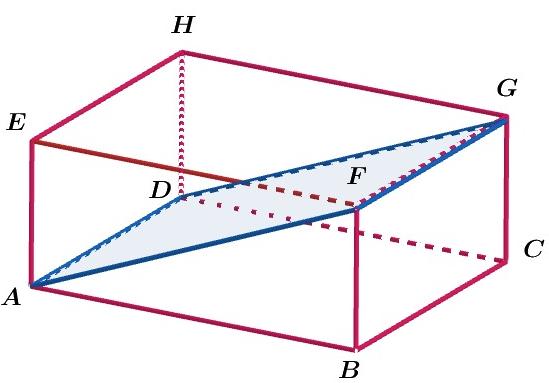
Jaring – jaring balok merupakan sisi – sisi balok yang direntangkan selepas dipotong dengan mengikuti jalur rusuk -rusuknya.
Ciri atau karakteristik dari jaring – jaring balok dapat kita lihat jika bentuk tersebut dilipat akan membentuk suatu bangun balok.
Jaring balok memiliki berbagai variasi, karena bentuk sisinya terdiri dari bangun datar persegi panjang.
Dengan cara memotong model balok pada setiap rusuk – rusuk tertentu, maka dapat menghasilkan suatu jaring -jaring balok.
Ciri – Ciri Balok
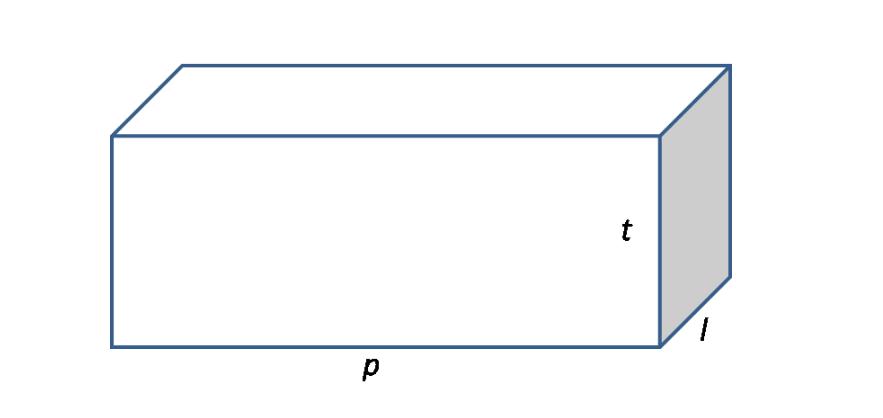
Untuk membedakan bangun balok dengan jenis bangun lainnya, maka terdapat beberapa ciri khusus seperti berikut ini:
- Mempunyai 12 rusuk.
- Mempunyai 8 titik sudut.
- Terdiri atas 6 sisi.
- Seluruh sudutnya pasti berbentuk siku – siku.
- Memiliki 12 diagonal bidang serta 4 diagonal dalam bentuk bangun ruang.
Perbedaan Balok dan kubus
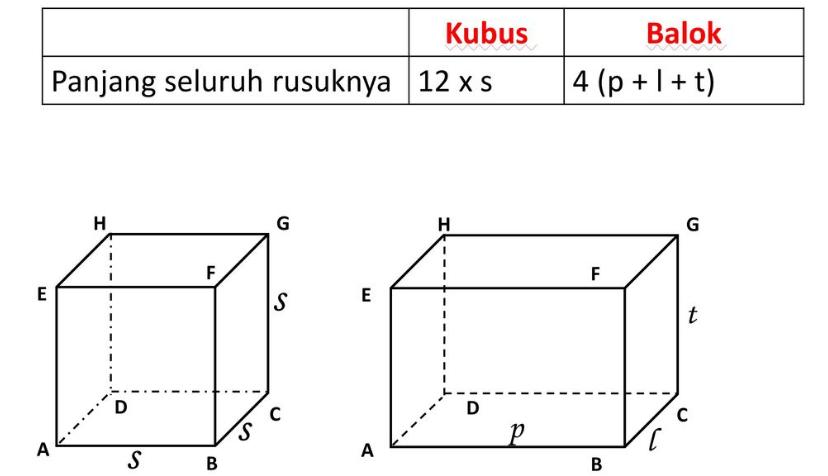
Berikut adalah perbedaan antara jaring – jaring balok dan kubus, antara lain:
- Perbedaannya terletak pada bentuk sisi pada keduanya. Cara pemotongan yang sama jika dimulai dari sisi yang berbeda maka dapat menghasilkan bentuk yang berbeda juga.
- Jaring – jaring kubus mempunyai bentuk sisi hanya dalam bentuk persegi, sementara pada sisi jaring – jaring balok terdiri atas persegi serta persegi panjang.
Sifat – Sifat Balok dan Bagian Balok
Berikut adalah beberapa sifat umum yang ada pada bangun balok, antara lain:
- Balok tersusun atas 3 pasang sisi yang sama (total memiliki 6 buah sisi).
- Pada masing – masing sisinya memiliki bentuk segiempat yakni persegi maupun persegi panjang.
- Paling sedikit harus memiliki 1 pasang sisi dengan bentuk yang berbeda.
- Memiliki 12 rusuk.
- Rusuk – rusuk yang sejajar memiliki ukuran yang sama.
- Memiliki 4 diagonal bidang.
- Diagonal bidang yang sejajar memiliki ukuran yang sama.
- Memiliki 4 diagonal ruang serta seluruhnya memiliki bentuk ukuran yang sama.
- Masing – masing bidang diagonalnya memiliki bentuk persegi panjang.
Rumus Balok
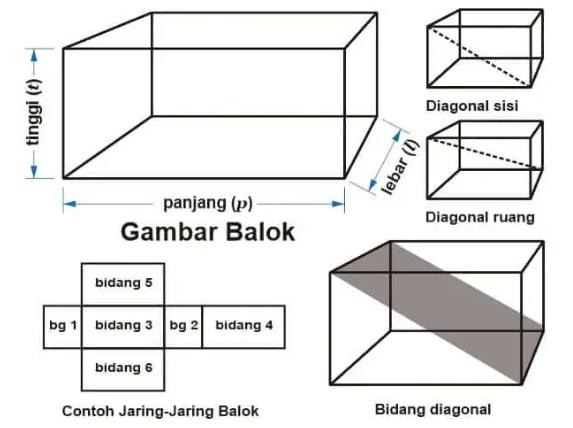
Keterangan:
- t = tinggi
- p = panjang
- l = lebar
Berikut adalah rumus lengkap yang berkaitan dengan bangun balok, antara lain:
| NAMA | RUMUS |
|---|---|
| Volume (V) | V = p × l × t |
| Luas Permukaan (L) | L = 2 × (p.l + p.t +l.t) |
| Panjang (p) | p = V ÷ l ÷ t |
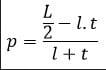 | |
| Lebar (l) | l = V ÷ p ÷ t |
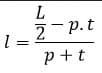 | |
| Tinggi (t) | t = V ÷ p ÷ l |
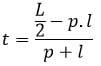 | |
| Diagonal bidang atau sisi (ds) | 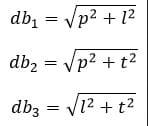 |
| Diagonal ruang (dr) | |
| Luas bidang diagonal (bd) | 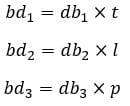 |
Praktek Membuat Jaring – Jaring Balok
Berikut adalah langkah – langkah cara untuk membuat jaring – jaring balok, antara lain:
1. Kalian siapkan kardus dengan bentuk balok dari karton seperti pada gambar yang ada di bawah ini:
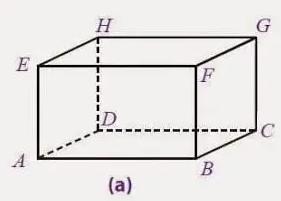
3. Gunting / kalian potong rusuk – rusuk balok tersebut pada titik – titik tertentu. Jangan kalian sisakan satu sisi bawah serta satu sisi samping.
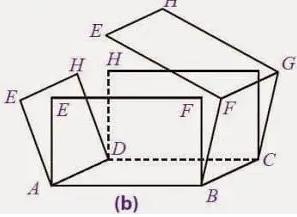
3. Rebahkan bagian balok yang telah dibuka itu di atas bidang yang datar, kemudian jaring – jaring balok selesai dibuat.
Apabila kalian melakukannya dengan benar, maka akan didapatkan bentuk seperti berikut:
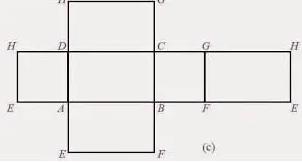
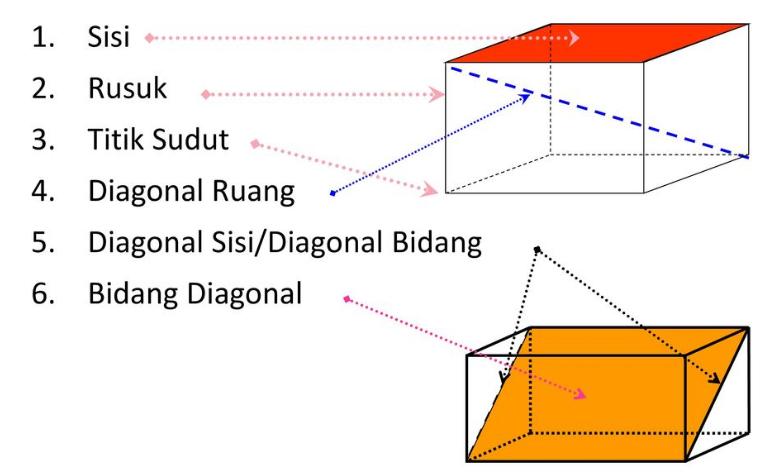
Unsur – Unsur Suatu Balok
Setelah membelah kardus menjadi sebuah jaring-jaring balok, maka dapat diketahui jaring-jaring balok tersusun dari:
- Sisi maupun bidang balok merupakan bagian yang membatasi balok. Balok mempunyai enam buah persegi panjang yang terdiri atas 3 persegi panjang sama besar.
- Persegi panjang ABCD sama seperti EFGH.
- Persegi panjang EHDA sama seperti BCGF.
- Persegi panjang ABFE sama seperti DCGH.
- Diagonal Bidang / Diagonal Sisi merupakan ruas garis yang mengaitkan antara dua titik sudut yang berhadapan di setiap bidang / sisi balok. Balok mempunyai 12 diagonal bidang / diagonal sisi.
- Rusuk merupakan garis potongan antara dua sisi bidang balok serta nampak seperti kerangka yang menyusun balok. Balok mempunyai total 12 rusuk.
- Titik Sudut merupakan titik potongan antara dua maupun tiga rusuk. Balok mempunyai total 8 titik sudut.
Sebab jaring – jaring balok serta jaring – jaring kubus mempunyai banyak sekali kemiripan, maka jaring – jaring balok juga mempunyai beberapa bentuk jaring – jaring sesuai dengan bagian rusuk mana yang dipotong.
Gambar Jaring – Jaring Balok
Berikut ada 54 gambar jaring – jaring balok yang harus kalian ketahui, antara lain:
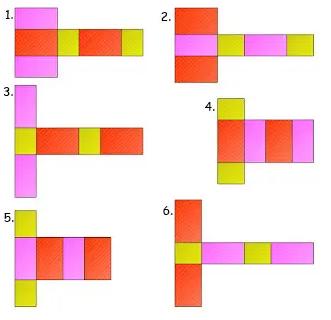
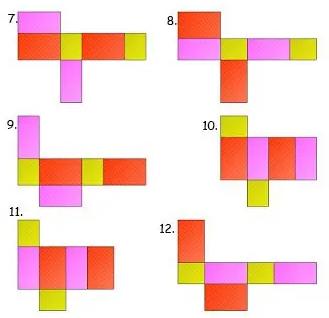
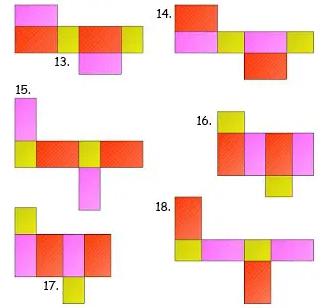
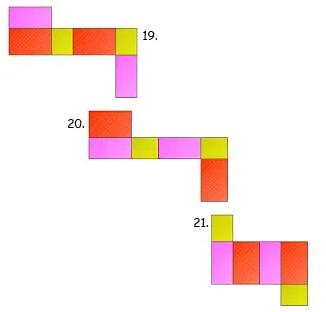
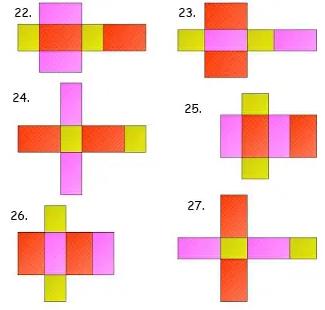
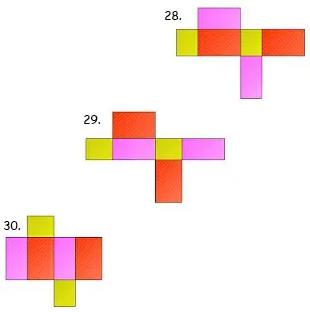
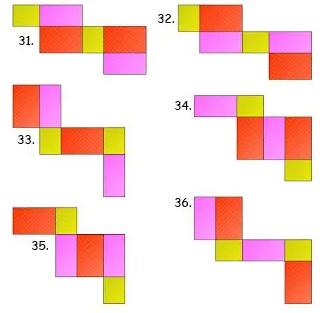
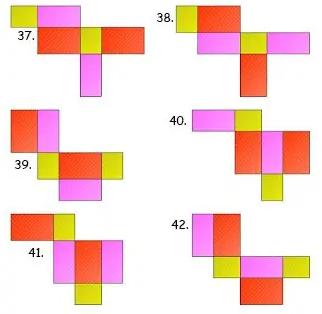
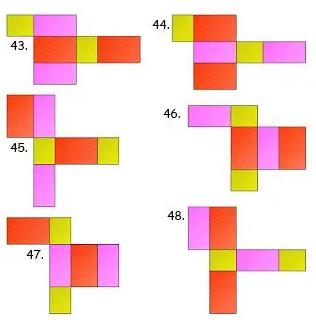
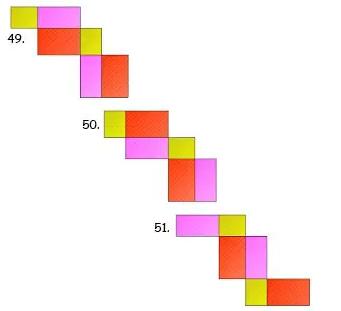
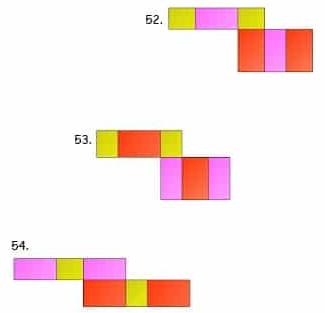
Contoh Soal
Untuk memudahkan kalian dalam memahami berbagai uraian di atas, berikut kami sajikan beberapa soal terkait bangun balok, antara lain:
1. Suatu balok memiliki volume 7120 cm³, apabila diketahui panjang balok adalah 10 cm serta lebar balok 8 cm. Hitunglah tinggi bangun balok tersebut!
Jawab:
Diketahui:
V = 720 cm³
p = 10 cm
l = 8 cm
Ditanya:
Tinggi balok (l) …?
Pembahasan:
l = V ÷ p ÷ l
l = 720 cm³ ÷ 10 cm ÷ 8 cm
l = 9 cm
Sehingga dapat diketahui panjang lebar balok tersebut yaitu 9 cm.
2. Hitunglah volume sera luas permukaan balok di bawah ini!
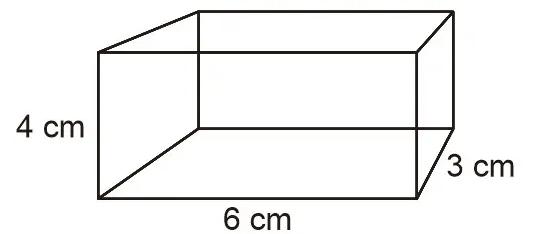
Jawab:
Diketahui:
p = 6 cm
l = 3 cm
t = 4 cm
Ditanya:
Volume (V) …?
Luas Permukaan (L) …?
Pembahasan:
Volume Balok
V = p × l × t
V = 6 cm × 3 cm × 4 cm
V = 72 cm³
Luas Permukaan Balok
L = 2 × (p.l + p.t +l.t)
L = 2 × ((6 cm × 3 cm) + (6 cm × 4 cm) + (3 cm × 4 cm))
L = 2 × (18 cm² + 24 cm² + 12²)
L = 2 × 54 cm²
L = 108 cm²
Sehingga volume balok tersebut yaitu 72 cm³ serta luas permukaan balok tersebut yaitu 108 cm².
3. Suatu balok memiliki panjang 20 cm, lebar 14cm, serta tinggi 10 cm. Hitunglah nilai luas permukaan dari balok tersebut?
Jawab:
Diketahui:
p = 20
l = 14
t = 10
Pembahasan:
Luas Permukaan Balok
= 2 (pl+pt+lt)
= 2 x (20×14) + (20×10) + (14 x 10)
= 2 x (280 + 200 + 140)
= 2 x 620
= 1240 cm²
Sehingga dapat diketahui luas permukaan balok tersebut adalah 1240 cm².
4. Apabila suatu balok memiliki volume 480 cm³, panjang serta lebar sisi berturut – turut 10cm dan 8cm. Hitunglah tinggi dari balok tersebut serta berapakah jumlah luas permukaannya?
Jawab:
Diketahui:
V = 480 cm³
P = 10
L = 8
Pembahasan:
Untuk menghitung tinggi dari balok tersebut, maka kalian gunakan rumus volume balok:
V = p x l x t
480 cm³= 10 x 8 x t
480 cm³= 80 t
t = 480 : 80
t = 6 cm
Sehingga dapat diketahui tinggi balok tersebut adalah 6 cm.
Lalu untuk menghitung luas permukaan balok adalah sebagai berikut:
Luas Permukaan Balok
= 2 (pl + pt + lt)
= 2 (10 x 8 + 10 x 6 + 8 x 6)
= 2 (80 + 60 + 48)
= 2 x 188
= 376 cm²
Sehingga dapat diketahui luas permukaan dari balok tersebut yaitu 376 cm².
5. Suatu balok memiliki volume 336 cm³, apabila diketahui panjang balok 8 cm serta tinggi balok 6 cm. Berapakah lebar balok tersebut?
Jawab:
Diketahui:
V = 336 cm³
p = 8 cm
t = 6 cm
Ditanya:
Lebar balok (l) …?
Pembahasan:
l = V ÷ p ÷ t
l = 336 cm³ ÷ 8 cm ÷ 6 cm
l = 7 cm
Sehingga panjang lebar balok tersebut yakni 7 cm.
6. Suatu balok memiliki luas permukaan 214 cm², apabila diketahui panjang balok 7 cm serta tinggi balok 5 cm. Hitunglah lebar balok tersebut!
Jawab:
Diketahui:
L = 214 cm²
p = 7 cm
t = 5 cm
Ditanya:
Lebar balok (l) …?
Pembahasan:
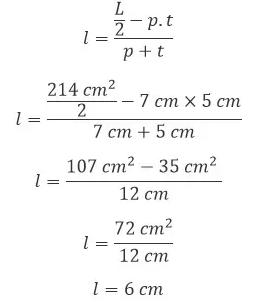
7. Hitunglah luas permukaan balok yang mempunyai panjang 9 cm, lebar 8 cm serta tinggi 7 cm.
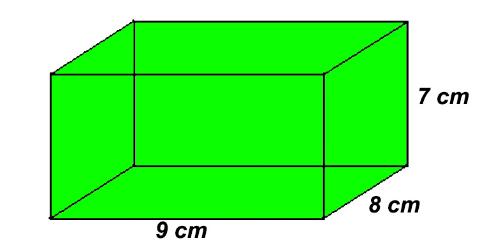
Jawab:
Diketahui:
p = 9 cm
l = 8 cm
t = 7 cm
Ditanyakan:
L = …?
Pembahasan:
L = 2 (pl + lt + pt)
L = 2 (9×8 + 8×7 + 9×7)
L = 2 (72 + 56 + 63)
L = 2 × 191
L = 382 cm²
Sehingga luas permukaan balok tersebut yaitu 382 cm².