Koordinat Cartesius juga sering disebut sebagai koordinat persegi. Istilah dari kata Cartesius yang dipakai adalah guna mengenang seorang ahli matematika sekaligus seorang filsuf dari Perancis yang bernama Rene Descartes.
Beliau merupakan seorang ahli yang memiliki peran yang besar dalam menggabungkan aljabar dan geometri.
Hasil penemuan descartes, koordinat cartesius ini sangat berpengaruh dalam perkembangan geometri analitik, kalkulus, dan kartografi.
Awal dari pemikiran dasar pemakaian sistem ini dikembangkan di tahun 1637 dalam dua tulisan dari karya Descartes.
Dalam karyanya Descartes Discourse on Method, beliau memperkenalkan saran baru guna menunjukan keadaan atau posisi titik dari suatu obyek pada sebuah permukaan.
Cara atau metode tersebut dengan memafaatkan dua sumbu yang saling tegak lurus antar satu dengan yang lain.
Dalam karya selanjutnya, La Géométrie, beliau juga memperdalam konsep-konsep yang sudah dikembangkannya.
Kemudian, barulah diperkenalkan untuk sistem-sistem koordinat lain seperti sistem koordinat polar.
Daftar Isi
Fungsi Koordinat Cartesius
Di dalam mata pelajaran matematika, sistem dari koordinat cartesius dipakai dalam menentukan setiap titik di dalam bidang dengan memakai dua bilangan yang biasa disebut sebagai koordinat x dan juga koordinat y dari titik tersebut.
Koordinat x sering juga disebutsebagai absis, sementara untuk koordinat y sering disebut juga sebagai ordinat.
Untuk mengartikan koordinat, dibutuhkan dua garis berarah yang tegak lurus satu sama lain [sumbu x serta sumbu y]. Serta panjang unit, yang dibuat tanda-tanda pada kedua sumbu tersebut.
Perhatikan baik-baik gambar di bawah ini:
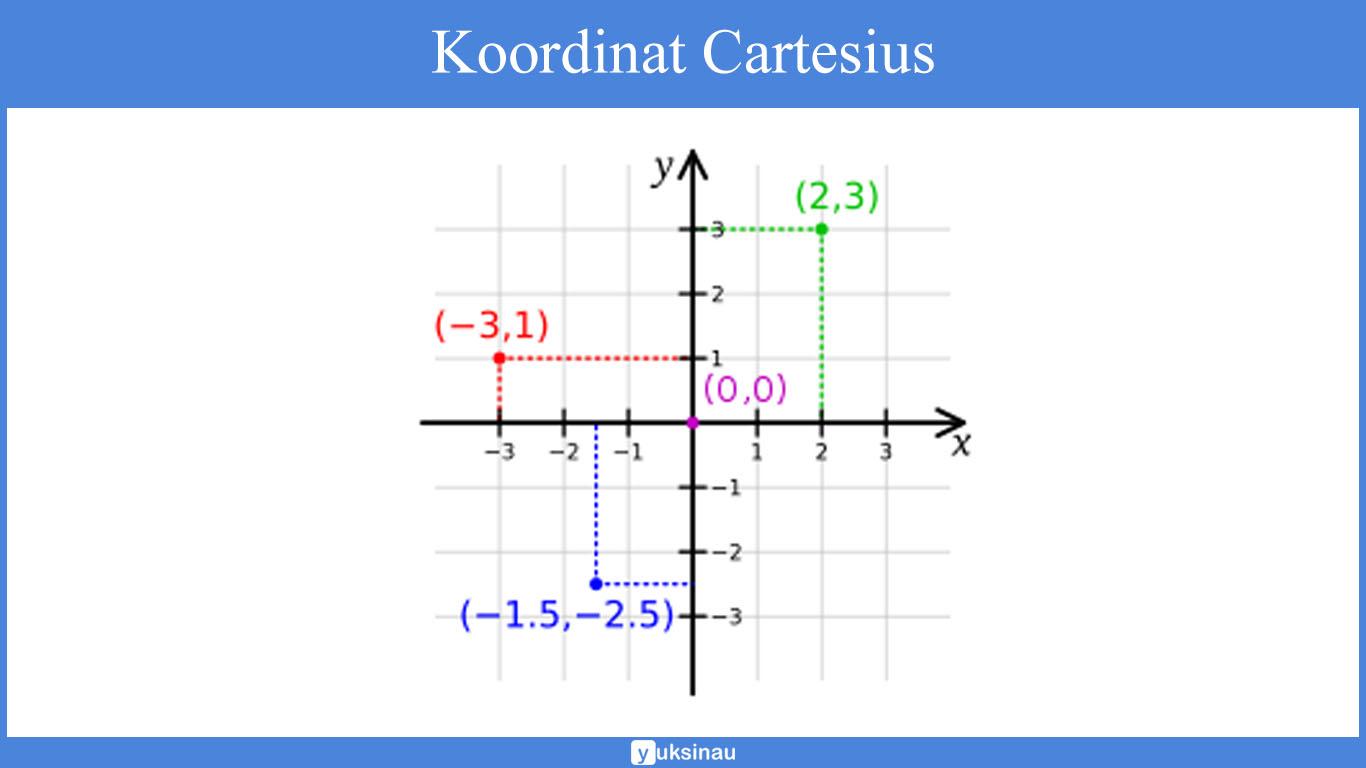
Dari gambar di atas bisa kita jumpati jika terdapat 4 titik yang sudah ditandai. Antara lain: [-3,1], [2,3], [-1.5,-2.5] dan [0,0]. Titik [0,0] disebut juga titik asal.
Dari gambar di atas juga bia kita lihat bahwa:
Sebab kedua sumbu bertegak lurus satu sama lain, maka bidang xy akan terbagi menjadi empat bagian yang disebut sebagai kuadran. Hal tersebut dapat dilihat pada pada Gambar di atas dengan ditandai adanya titik [-3,1], titik [2,3], titik [-1.5,-2.5].
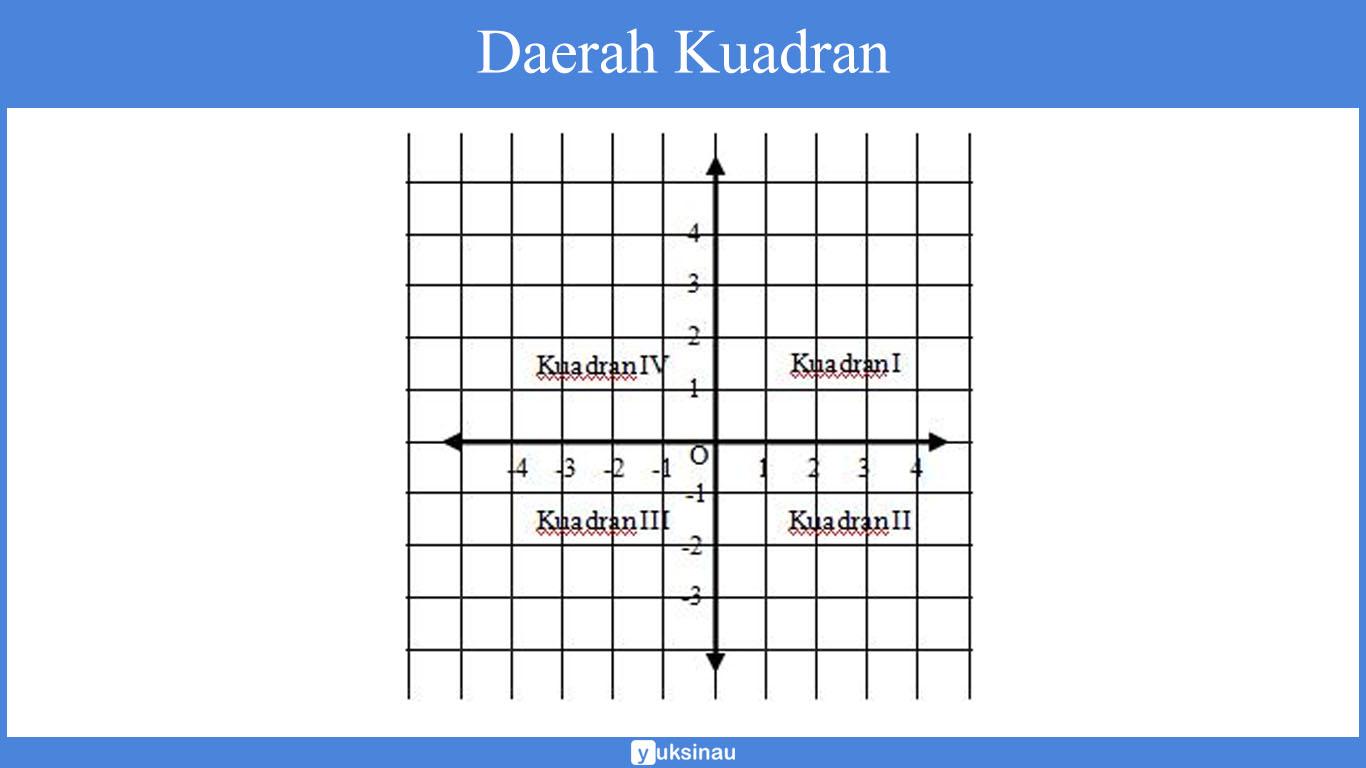
Menurut dari konvensi yang berlaku, keempat daerah kuadran tersebut diurutkan mulai dari yang kanan atas [kuadran I], melingkar melawan arah jarum jam.
Dalam kuadran I, kedua koordinat (x dan y) akan bernilai positif.
Dalam kuadran II, koordinat x akan bernilai negatif dan koordinat y akan bernilai positif.
Dalam kuadran III, kedua koordinat akan bernilai negatif.
Serta dalam kuadran IV, koordinat x bernilai positif dan y akan bernilai negatif .
Titik [2,3] berada pada kuadran I, tititk [-3,1] berada pada kuadran II dan titik [-1.5,-2.5] berada pada kuadran III.
Atau secara umum, keempat daerah kuadran tersebut diurutkan mulai dari yang kanan atas [kuadran I], melingkar melawan arah jarum jam.
Dalam kuadran I, kedua koordinat [x dan y] akan bernilai positif.
Dalam kuadran II, koordinat x akan bernilai negatif serta koordinat y akan bernilai positif.
Dalam kuadran III, kedua koordinat akan bernilai negatif, serta dalam kuadran IV, koordinat x akan bernilai positif dan y negatif [perhatikan kembali pada gambar di atas].
| Kuadran | Nilai x | Nilai y |
| I | bernilai positif [> 0] | bernilai positif [> 0] |
| II | bernilai negatif [< 0] | bernilai positif [> 0] |
| II | bernilai negatif [< 0] | bernilai negatif [< 0] |
| IV | bernilai positif [> 0] | bernilai negatif [< 0] |
Sistem dari koordinat cartesius dalam dua dimensi pada umumnya diartikan dengan menggunakan dengan dua sumbu yang saling bertegak lurus antar satu dengan yang lain.
Di mana kedua letak dari sumbu tersebut berada pada satu bidang yakni bidang xy. Sumbu horizontal akan diberi label x, semetara untuk sumbu vertikal diberi label y.
Titik pertemuan antara kedua sumbu, titik asal, pada umumnya akan diberi label 0.
Pada masing-masing sumbu juga memilikiu besaran panjang unit, serta masing-masing panjang tersebut akan diberi tanda sehingga akan membentuk semacam grid.
Untuk mendeskripsikan sebuah titik tertentu dalam sistem koordinat dua dimensi, maka nilai x ditulis [absis], kemudia diikuti dengan nilai y [ordinat].
Dengan begitu, format yang digunakan akan selalu [x,y] serta urutannya tidak akan dibalik-balik.
Sistem koordinat cartesius bisa juga dipakai dalam pada dimensi-dimensi yang lebih tinggi.
Sebagai contoh: 3 [tiga] dimensi, dengan memakai tiga sumbu yakni sumbu x, sumbu y, dan sumbu z.
Apabila dalam dua dimensi garisnya berada dalam bidang xy, maka pada sistem koordinat tiga dimensi, akan ditambahkan sumbu lain yang sering diberi label z.
Di mana sumbu z ini berada saling tegak lurus dengan sumbu x dan sumbu y [dengan kata lain, sumbu x, sumbu y, serta sumbu z saling tegak lurus atau ortogonal].
Manfaat Cartesius
Dengan memakai sistem koordinat cartesius, bentuk-bentuk geometri seperti kurva bisa kita gambarkan dengan menggunakan persamaan aljabar.
Dalam era modern ini koordinat cartesius telah banyak dimanfaatkan penggunaanya.
Berikut ini adalah beberapa manfaat dari koordinat cartesius, antara lain yaitu:
Pertama:
Di dalam kehidupan sehai-hari sering kali kita menemukan gambar denah maupun gambar peta.
Di mana fungsi dari peta sendiri untuk memudahkan kita dalam mencari suatu lokasi atau tempat ataupun wilayah.
Begitu pula ketika kita hendak mengirim surat kepada seseorang. Dalam mengirimkan surat kepada seseorang kita harus nengetahui alamat tujuannya secara lengkap dan juga benar.
Hal tersebut bertujuan guna mempermudah pengiriman dari surat itu sendiri.
Sehingga, apabila kita mencantumkan alamat dengan benar dan lengkap maka surat pun akan lebih cepat sampai. Di peta juga terdapat garis lintang dan juga garis bujur.
Kedua:
Di dalam kehidupan sehari-hari dalam bidang koordinat cartesius sangat mutlak diperlukan.
Salah satunya yaitu dalam soal penerbangan.
Seorang pilot bisa menerbangkan pesawat terbangnya tanpa bertabrakan satu sama lainnya serta juga bisa mengetahui jika pesawat telah sampai tujuan.
Hal tersebut disebabkan pesawat terbang itu telah dilengkapi dengan alat yang canggih seperti radar sebagai alat pendeteksi, kompas sebagai petunjuk arah, dan juga radio sebagai alat komunikasi.
Oleh sebab itu seorang pilot harus memahami cara membaca serta menentukan letak suatu tempat dalam bidang koordinat cartesius.
Ketiga:
Dalam pelajaran ilmu-ilmu sosial, sering juga kita temui peta suatu provinsi atau bahkan peta dari sebuah negara.
Posisi dari sebuah kota, gunung, danau, lapangan terbang, bisa kita ibaratkan sebagai kadudukan. Untuk memudahkan pembacaan peta, peta telah dilengkapi dengan garis bantu yang mendatar dan juga tegak atau garis lintang dan garis bujur.
Dasar pembuatan garis tersebut yang mana adalah dasar dari bidang koordinat.
Menentukan Titik pada Sistem Koordinat Cartesius
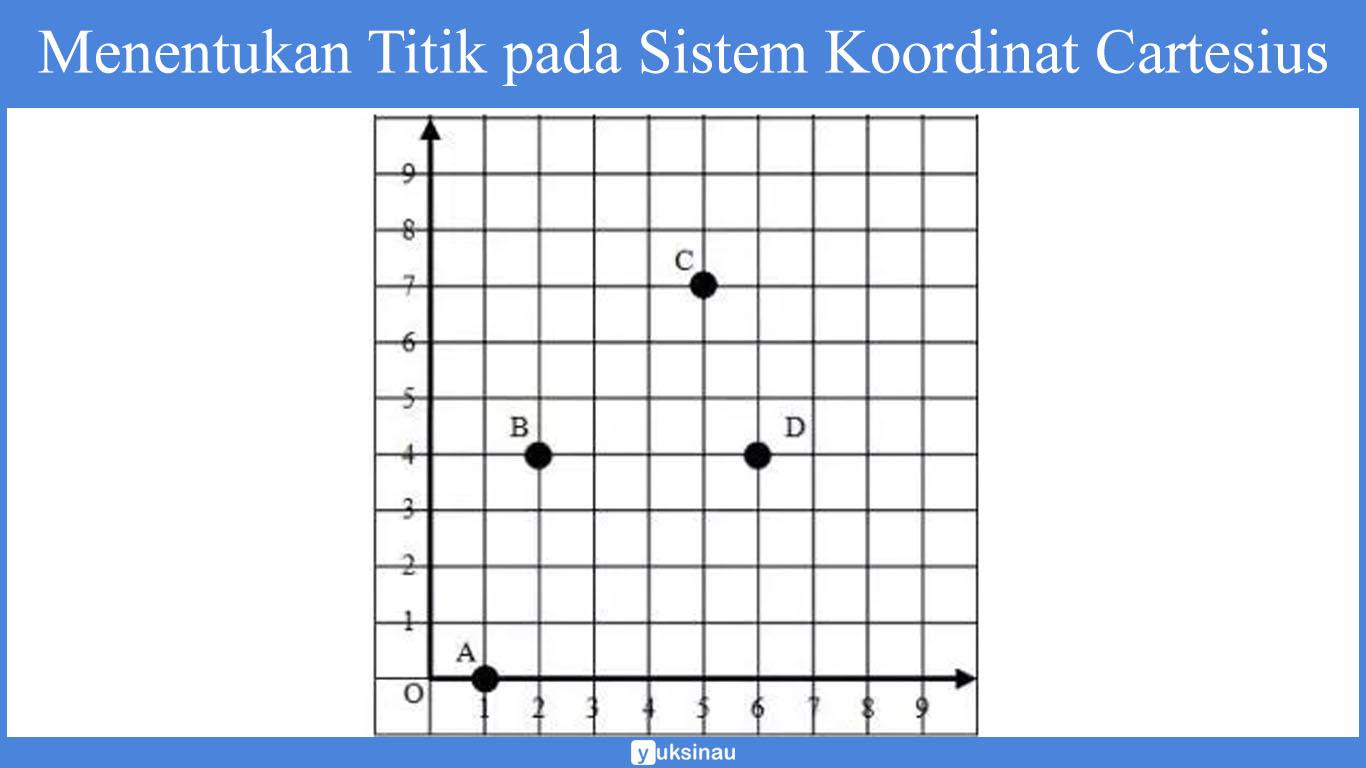
Bidang datar di atas disebut sebagai bidang koordinat yang dibentuk oleh garis tegak Y (sumbu Y) serta garis mendatar X (sumbu X).
Titik akan saling berpotongan diantara garis Y dan garis X yang disebut sebagai pusat Koordinat (titik O).
Dalam koordinat tersebut dikenal dengan bidang koordinat Cartesius. Seperti yang telah dijelaskan di atas, bidang koordinat Cartesius dipakai dalam menentukan letak suatu titik yang dinyatakan dalam pasangan bilangan.
Perhatikan titik A, B, C, dan D dalam bidang tersebut. Untuk menentukan posisinya, mulailah dari titik O. Lalu, bergerak mendatar kearah kanan (sumbu X), kemudian bergerak ke atas (sumbu Y).
Posisi dari titik pada bidang koordinat Cartesius ditulis dalam bentuk pasangan bilangan (x, y), di mana:
- x disebut sebagai absis, serta
- y disebut ordinat.
Dalam bidang koordinat tersebut, maka:
- Titik A berada di koordinat (1,0), ditulis dengan A(1,0).
- Titik B berada pada koordinat (2,4), ditulis dengan B(2,4).
- Titik C berada pada koordinat (5,7), ditulis dengan C(5,7).
- Serta titik D berada pada koordinat (6,4) ditulis dengan D(6,4).
Dalam bidang koordinat Cartesius bisa kita perluas menjadi seperti pada gambar di bawah ini:
Sebagai contoh:
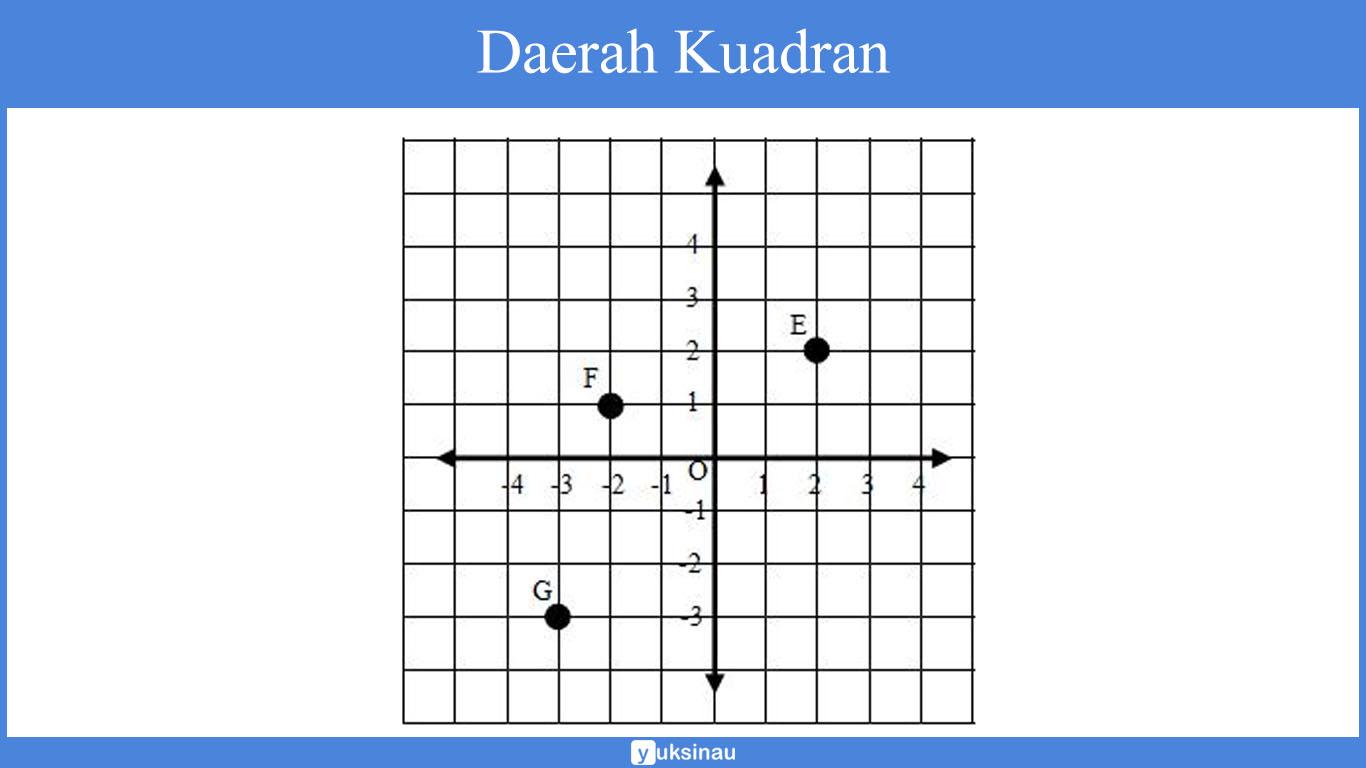
- Koordinat titik E yaitu (2,2)
- Koordinat titik F yaitu (-2,1), didapatkan dengan cara bergerak mendatar ke kiri dimulai dari titik O sebanyak dua satuan kemudia tegak ke atas sebanyak satu satuan.
- Koordinat titik G yaitu (-3,-3), di dapatkan dengan bergerak mendatar ke kiri diawali dari titik O sebanyak tiga satuan kemudian tegak ke bawah sebanyak tiga satuan.
Contoh Soal dan Pembahasan
Soal 1.
Ordinat dari titik A (9, 21) adalah…
a. -9
b. 9
c. -21
d. 21
Jawab:
Pada umumnya, penulisan suatu titik = (absis, ordinat). Dalam soal di atas titik A (9, 21) menunjukkan jika:
Absis = 9
Ordinat = 21
Jawaban yang tepat yaitu D.
Soal 2.
Diketahui titik P (3, 2) dan Q (15, 13). Koordinat relatif titik Q terhadap P adalah…
a. (12, 11)
b. (12, 9)
c. (18, 11)
d. (18, 13)
Jawab:
Koordinat relatif titik Q ke titik P bisa kita cari dengan cara mengurangkan:
a. Absis Q dikurangi absis P
b. Ordinat Q dikurangi ordinat P
Sehingga, koordinat relatif Q terhadap P yaitu:
(15 – 3 , 13 – 2) = (12, 11)
Sehingga,jawaban yang tepat adalah A.
Soal 3.
Titik A (3, 2), B (0, 2), dan C (-5, 2) merupakan titik-titik yang dilewati oleh garis p. Apabila garis q merupakan garis yang sejajar dengan garis p, maka garis q akan…
a. Sejajar dengan sumbu x
b. Sejajar dengan sumbu y
c. Tegak lurus dengan sumbu x
d. Tegak lurus dengan sumbu y
Jawab:
Untuk memudahkan kita dalam menjawab soal di atas, mari kita gambar pada bidang Cartesius:
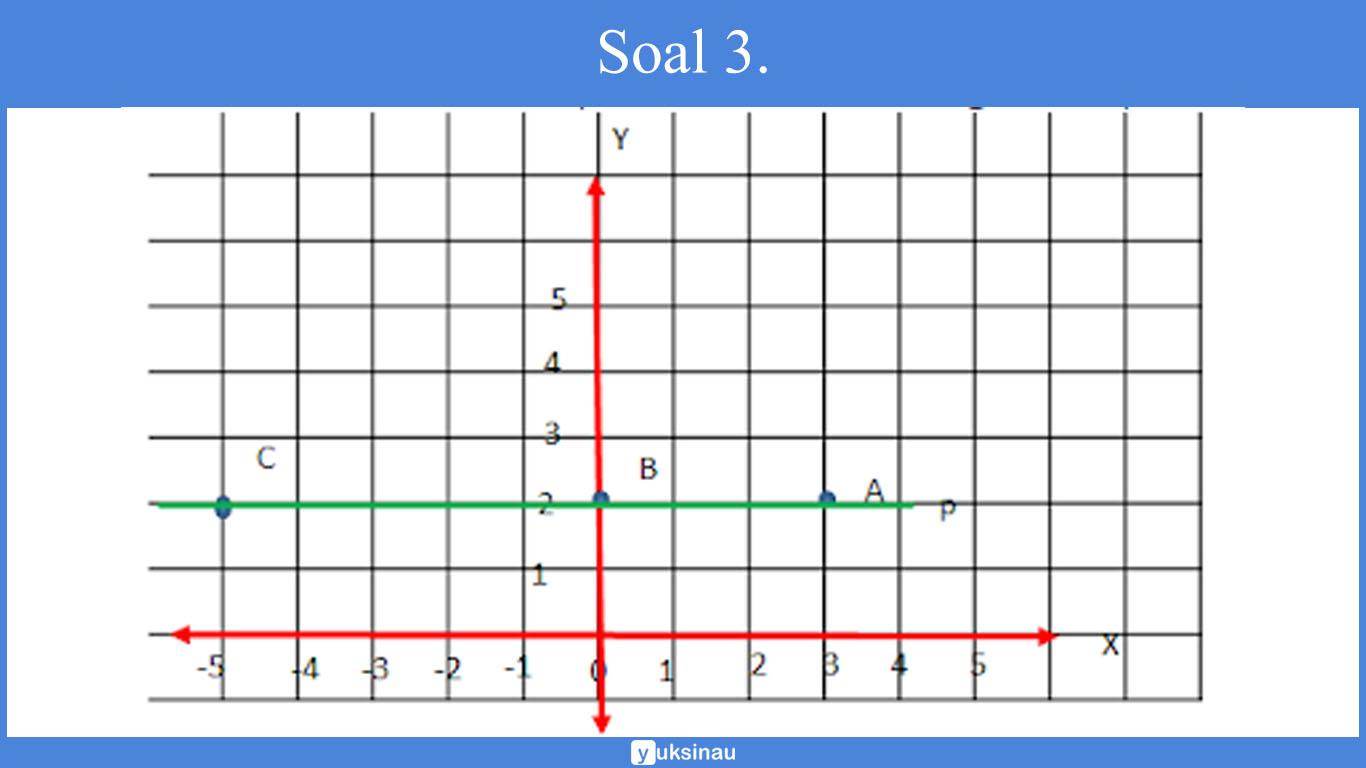
Dalam gambar di atas terlihat jikga garis p sejajar dengan sumbu X. Sebab garis q sejajar dengan garis p, maka garis q juga sejajar dengan sumbu X.
Sehingga, jawaban yang tepat adalah A.
Soal 4.
Diketahui garis p dan q merupakan dua garis lurus yang tidak mempunyai titik potong walaupun telah diperpanjang hingga tak terhingga.
Kedudukan dari garis p dan q yaitu…
a. Berimpit
b. Sejajar
c. Bersilangan
d. Berpotongan
Jawab:
Dua buah garis yang tidak mempunyai titik potong walaupun diperpanjang merupakan dua garis yang saling sejajar.
Sehingga, jawaban yang tepat adalah B.
Soal 5.
Berdasarkan gambar di bawah ini, bisa dinyatakan bahwa:
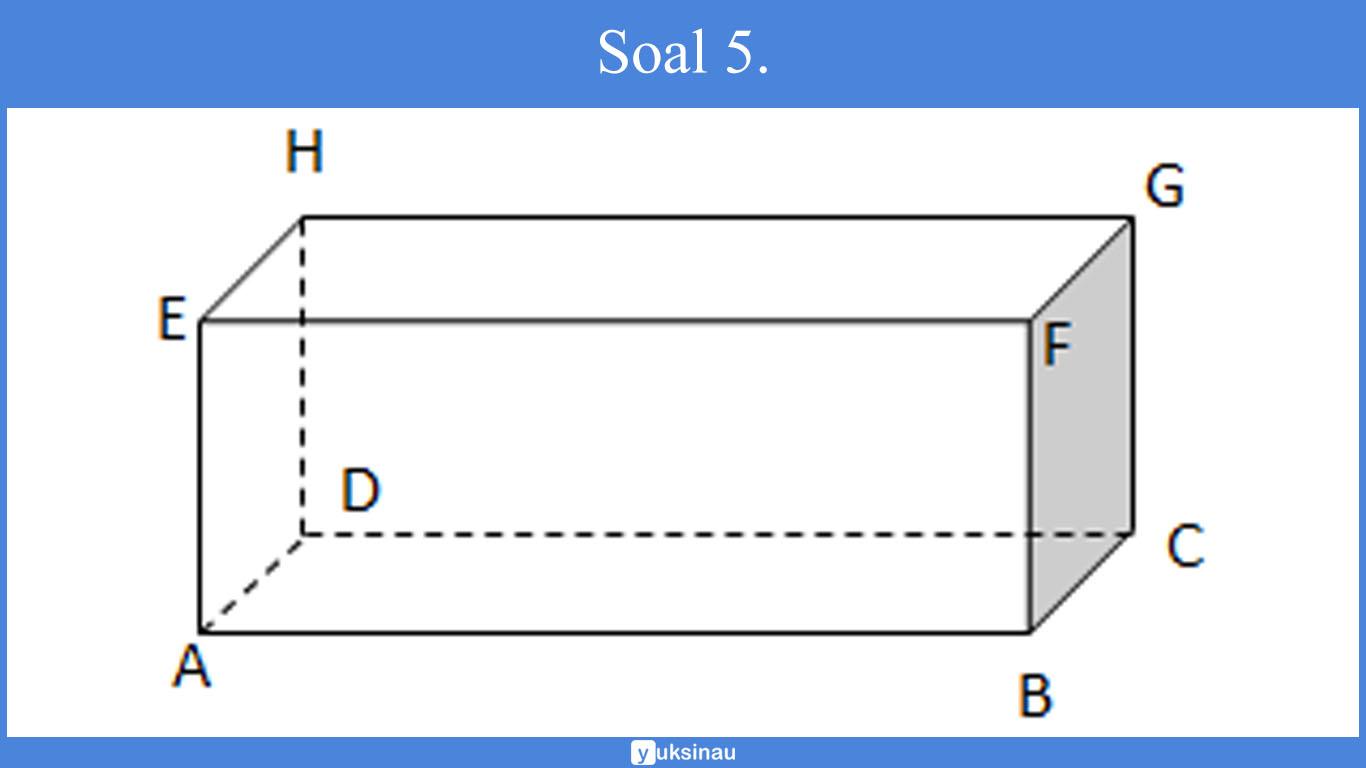
(i) AB sejajar dengan EF.
(ii) BC bersilangan dengan GC
(iii) AD berimpit dengan BC.
(iv) EF berpotongan dengan GF.
Dari pernyataan di atas, yang benar yaitu…
a. (i) dan (ii)
b. (ii) dan (iii)
c. (iii) dan (iv)
d. (i) dan (iv)
Jawab:
Perhatikan gambar balok di atas:
a. AB sejajar EF , maka (i) benar
b. BC berpotongan dengan GC di titik C, maka (ii) salah
c. AD sejajar dengan BC, maka (iii) salah
d. EF berpotongan dengan GF di titik F, maka (iv) benar
Sehingga, jawaban yang benar adalah D.
Soal 6.
Besar <P = 113 derajat maka sudut P adalah sudut…
a. Refleks
b. Tumpul
c. Siku-siku
d. Lancip
Jawab:
Sudut P besarnya 113 derajat, yang berarti sudut P merupakan sudut tumpul.
Sebab sudut tumpul merupakan sudut yang berada dalam kisaran 90 derajat sampai 180 derajat.
Sehingga, jawaban yang benar adalah B.
Soal 7.
Besar sudut pada jarum jam saat menunjukkan pukul 03.00 adalah…
a. 180°
b. 90°
c. 60°
d. 30°
Jawab:
Pada saat pukul 03.00, jarum pendek akan menunjuk pada angka 3 sedangkan jarum panjang akan menunjuk angka 12, oleh karena itu sudut yang dibentuk yaitu 90 derajat.
Sehingga, jawaban yang benar adalah B.
Soal 8.
Perhatikan gambar di bawah ini!
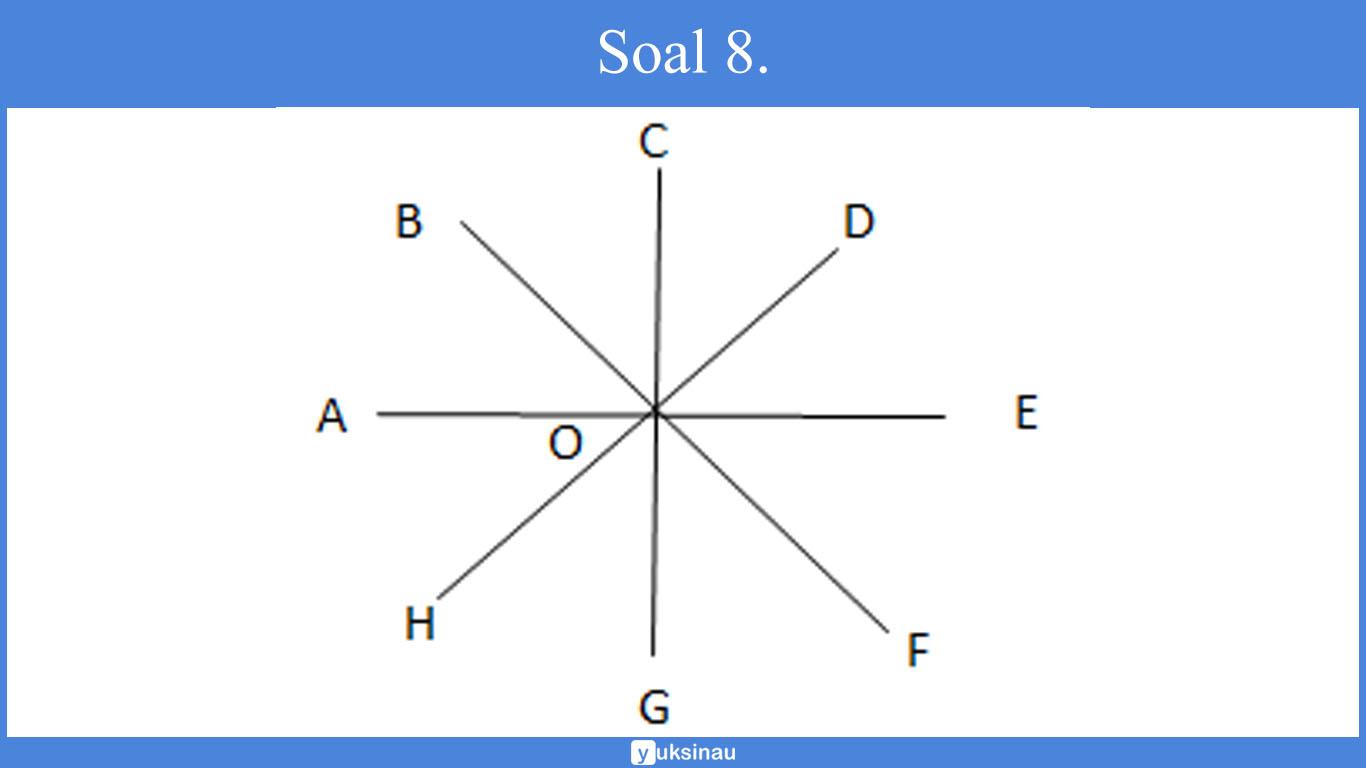
Pasangan sudut yang bertolak belakang yaitu…
a. <BOD dan <EOG
b. <AOH dan <EOC
c. <HOG dan <DOC
d. <AOF dan <FOE
Jawab:
Mari kita bahas satu persatu dari opsi di atas:
a. Opsi A salah, sebab yang seharusnya adalah <BOD bertolak belakang dengan <FOH
b. Opsi B salah, sebab yang seharusnya adalah <AOH bertolak belakang dengan <EOD
c. Opsi C benar, yakni <HOG bertolak belakang dengan <DOC
d. Opsi D salah, sebab yang seharusnya adalah <AOF bertolak belakang dengan <EOB.
Sehingga, jawaban yang benar adalah C.
Soal 9.
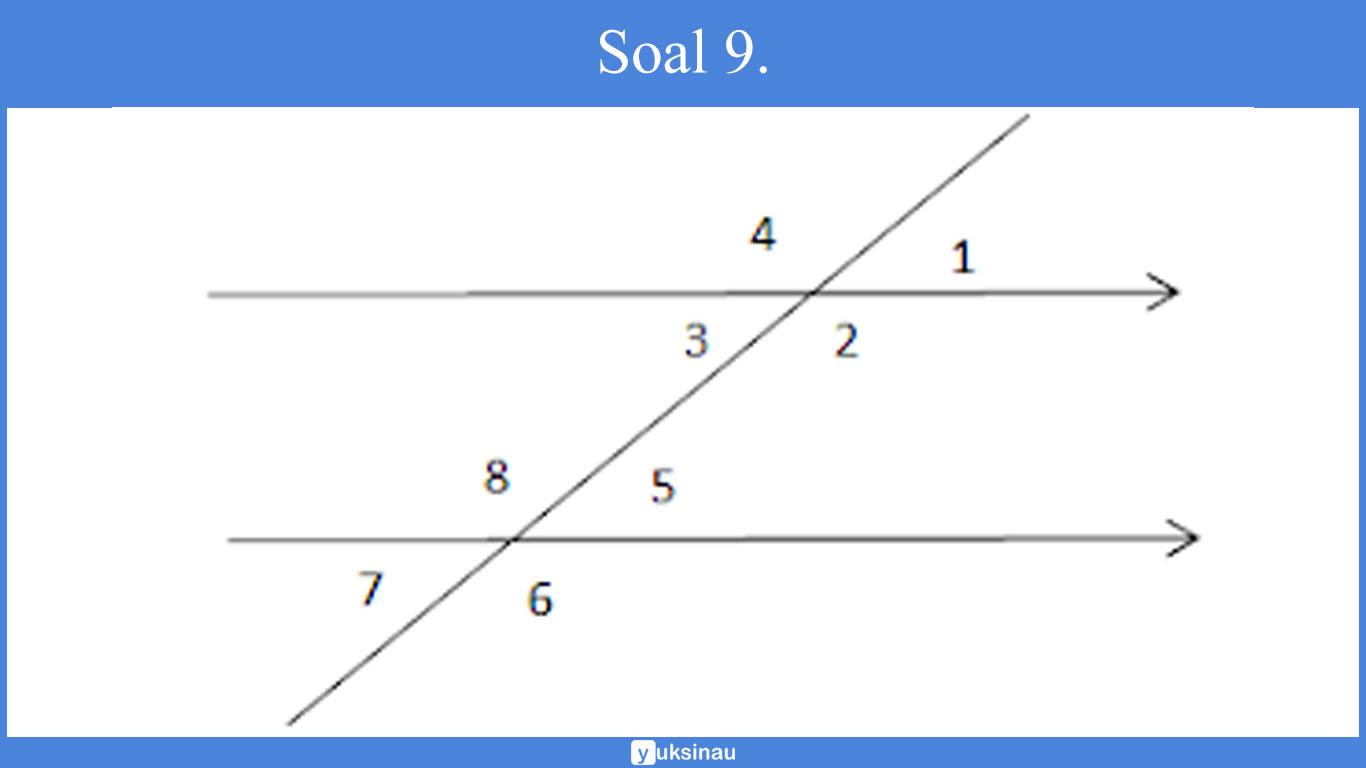
Pasangan sudut dalam berseberangan pada gambar di atas yaitu…
a. 2 dan 8
b. 4 dan 6
c. 3 dan 8
d. 1 dan 5
Jawab:
Mari kita bahas satu persatu dari opsi di atas:
a. 2 dan 8 merupakan pasangan sudut dalam berseberangan.
b. 4 dan 6 merupakan pasangan sudut luar berseberangan.
c. 3 dan 8 merupakan pasangan sudut dalam sepihak.
d. 1 dan 5 merupakan pasangan sudut sehadap.
Sehingga, jawaban yang benar adalah A.
Soal 10.
Komplemen dari sudut 48 dejarat yaitu…
a. 42°
b. 52°
c. 68°
d. 138°
Jawab:
Komplemen = 90 – 48 = 42
Sehingga, jawaban yang benar adalah A.
Demikianlah ulasan singkat kali ini mengenai Koordinat Cartesius yang dapat kami sampaikan. Semoga ulasan di atas mengenai Koordinat Cartesius dapat kalian jadikan sebagai bahan belajar kalian.
Satu pemikiran pada “Koordinat Cartesius”