Seringkali kita dihadapkan pada situasi yang mengharuskan kita untuk menentukan rata-rata, nilai tengah, atau datum dengan frekuensi terbanyak. Dalam menentukan ketiga hal tersebut, terdapat mean, median, modus yang mampu membantu kita dalam menyelesaikannya.
Oleh karena itu, yuk pelajari mean, median, modus melalui artikel ini, supaya kita tidak mengalami kesulitan saat menghadapi situasi tersebut. Selamat belajar!
Daftar Isi
Pengertian Mean, Median, dan Modus

1. Mean
Mean atau rata-rata merupakan wakil dari sekumpulan banyak data. Mean dilambangkan dengan x̄ (dibaca x bar) dan dapat dihitung nilainya dari data tunggal maupun data tunggal berkelompok.
2. Median
Median (Me) atau kuartil merupakan nilai tengah dari kumpulan data setelah data tersebut diurutkan dari yang terkecil sampai terbesar. Apabila suatu kumpulan data berjumlah ganjil, maka mediannya terletak pada data ke 1/2(n+1) dengan n sebagai jumlah data.
Namun, jika suatu kumpulan data berjumlah genap, maka mediannya terletak pada dan data n/2 dan data (n/2) + 1 adalah jumlah data.
3. Modus
Modus (Mo) yaitu datum yang sering muncul dan menjadi ukuran pemusatan untuk menyatakan fenomena dengan frekuensi terbanyak.
Jika data yang diperoleh merupakan data tunggal berkelompok atau data yang disajikan dalam tabel, maka kamu bisa langsung melihat datum dengan frekuensi terbanyak.
Baca: Limit Matematika
Penerapan Mean, Median, dan Modus
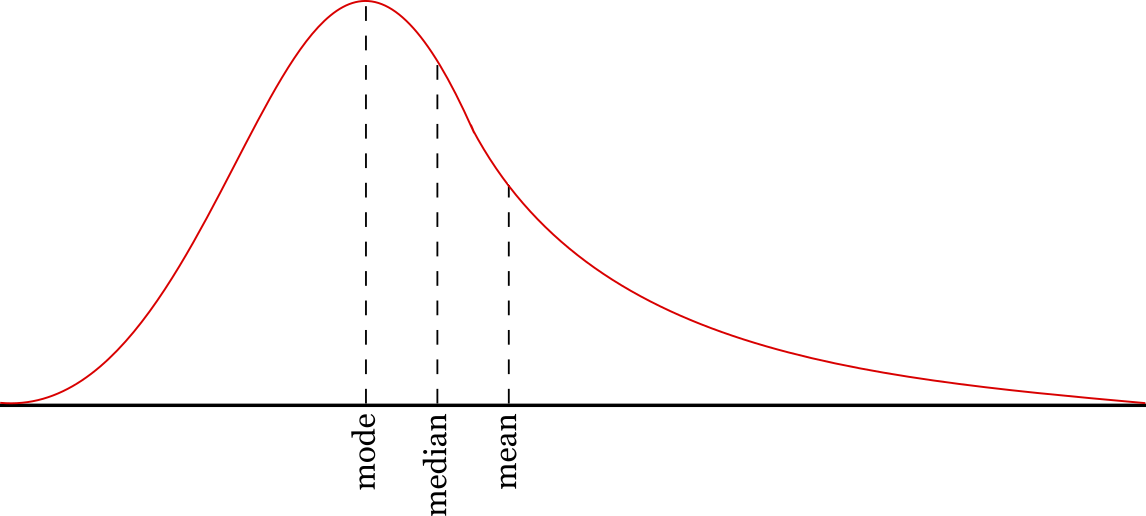
Mean, median, modus biasanya diperlukan untuk menganalisis hasil atau pengumpulan data. Setelah data berhasil diperoleh, kemudian data akan diolah menggunakan metode statistik.
Misalnya, ketika mendapatkan data terkait hasil panen padi setiap tahunnya. Rata-rata atau mean dapat digunakan untuk menentukan berapa rata-rata ton padi yang dihasilkan per tahunnya. Sedangkan, Median digunakan apabila ingin mencari nilai tengah dari hasil panen.
Modus digunakan untuk mengetahui berapa banyak ton padi yang diperoleh pada jumlah tertentu atau untuk menentukan frekuensi paling banyak dari jumlah hasil panen padi.
Untuk lebih jelasnya, yuk pelajari rumus dari mean, median, modus!
Rumus Mean, Median, dan Modus
Rumus Mean
1. Data Tunggal
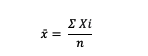
x̄ = nilai rata-rata (mean)
∑Xi = jumlah dari nilai data ke-i
n = banyaknya data
2. Data Berkelompok
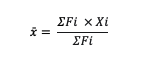
x̄ = nilai rata-rata (mean)
Fi = frekuensi dari kelompok data ke-i
Xi = nilai tengah dari kelompok data ke-i
Baca: Turunan Matematika
Rumus Median
1. Data tunggal dengan jumlah datum ganjil
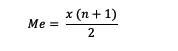
Dalam menentukan median jika datum berjumlah ganjil, kamu bisa menggunakan rumus berikut:
Me = median
x = datum
n = banyaknya data
2. Data tunggal dengan datum genap
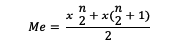
Jika datum ternyata berjumlah genap, gunakan rumus berikut untuk menentukan median:
Me = median
x = datum
n = banyaknya data
3. Data berkelompok
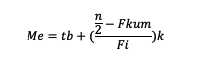
Me = median
tb = tepi bawah kelas median
n = banyaknya data
Fkum = frekuensi kumulatif sebelum kelas median
Fi = frekuensi kelas median
k = panjang kelas
Rumus Modus
Dalam menentukan modus pada data tunggal, kamu bisa membuat tabel frekuensi agar mudah dalam melihat frekuensi terbanyak pada tiap datum. Sedangkan pada data berkelompok, kamu bisa menggunakan rumus di bawah ini:
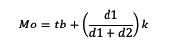
Mo = modus pada data berkelompok
tb = tepi bawah kelas modus
d1 = frekuensi kelas modus yang dikurangi dengan frekuensi kelas sebelumnya
d2 = frekuensi kelas modus yang dikurangi dengan frekuensi kelas sesudahnya
k = panjang kelas
Baca: Logaritma
Contoh Soal Mean, Median, dan Modus
Setelah khatam dengan materi mean, median, modus kurang afdol rasanya jika belum melatih pemahaman tersebut dengan latihan soal. Yuk kerjakan soal berikut ini!
1. Diketahui deretan angka 163, 167, 168, 170, 175, 180, 185. Berapakah nilai mediannya?
- 168
- 170
- 185
- 163
Jawab:
163, 167, 168, 170, 175, 180, 185
Jadi, nilai median dari deretan angka tersebut adalah 170 (B)
2. Perhatikan tabel berikut!
| Nilai | Frekuensi |
| 105 | 5 |
| 95 | 2 |
| 80 | 3 |
| 75 | 1 |
| 65 | 1 |
| 60 | 2 |
Nilai yang sering muncul dari tabel di atas yaitu?
- 105
- 95
- 80
- 75
- 60
Jawab:
Dilihat dari tabel, nilai dengan frekuensi terbanyak yaitu 105 (A)
3. Diketahui deretan angka 150, 165, 168, 168, 175, 177, 180, 188. Berapakah nilai mediannya?
- 188
- 175
- 165
- 171,5
- 177
Jawab:
150, 165, 168, 168, 175, 177, 180, 188
Gunakan rumus:
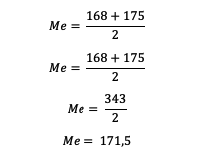
Jadi, nilai median dari deretan angka tersebut adalah 171, 5 (D)
4. Nilai modus dari 40,40,45,45,45,50,55,65,65,70 yaitu …
- 70
- 65
- 55
- 50
- 45
Jawab:
| Angka | Frekuensi |
| 40 | 2 |
| 45 | 3 |
| 50 | 1 |
| 55 | 1 |
| 65 | 2 |
| 70 | 1 |
Modus atau nilai dengan frekuensi terbanyak dari angka-angka tersebut yaitu 45 (E)
Cermati tabel berikut untuk menjawab pertanyaan nomor 5, 6, dan 7!
| Nilai | Frekuensi |
| 10-20 | 2 |
| 21-31 | 8 |
| 32-42 | 15 |
| 43-53 | 7 |
| 54-64 | 10 |
| 65-75 | 3 |
5. Berapakah mean dari data di atas?
- 41,77
- 41,87
- 42,77
- 42,87
- 43,77
Jawab:
| Nilai | Frekuensi | Fkum | Xi | Fi.X.Xi |
| 10-20 | 2 | 2 | 15 | 30 |
| 21-31 | 8 | 10 | 26 | 208 |
| 32-42 | 15 | 25 | 37 | 555 |
| 43-53 | 7 | 32 | 48 | 336 |
| 54-64 | 10 | 42 | 59 | 590 |
| 65-75 | 3 | 45 | 70 | 210 |
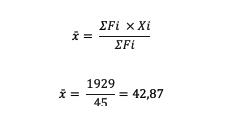 Jadi, nilai mean atau rata-rata data tersebut yaitu 42,87 (D)
Jadi, nilai mean atau rata-rata data tersebut yaitu 42,87 (D)
6. Berapakah median dari tabel di atas?
- 40,27
- 40,37
- 40,47
- 40,57
- 40,67
Jawab:
| Nilai | Frekuensi | Fkum | Xi | Fi.X.Xi |
| 10-20 | 2 | 2 | 15 | 30 |
| 21-31 | 8 | 10 | 26 | 208 |
| 32-42 | 15 | 25 | 37 | 555 |
| 43-53 | 7 | 32 | 48 | 336 |
| 54-64 | 10 | 42 | 59 | 590 |
| 65-75 | 3 | 45 | 70 | 210 |
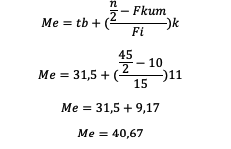 Jadi, median dari data di atas adalah 40,67 (E)
Jadi, median dari data di atas adalah 40,67 (E)
7. Berapakah modus dari tabel di atas?
- 35,53
- 35,63
- 36,63
- 36,53
- 36,73
Jawab:
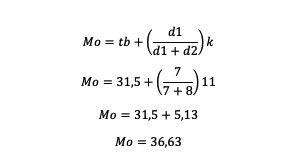
Jawab:
Nilai modus yang didapatkan yaitu 36,63 (C)
Kesimpulan
Dalam statistika, terdapat data tunggal dan data berkelompok. Kita dapat mencari mean, median, modus dari data tunggal maupun data berkelompok menggunakan rumus-rumus yang telah dijelaskan di atas.
Seperti yang sudah dijelaskan, mean merupakan rata-rata atau perwakilan dari sebuah data. Mean adalah nilai tengah dari sebuah data. Sedangkan modus adalah datum yang paling sering muncul atau yang memiliki frekuensi terbanyak.
Dalam kehidupan sehari-hari, kita banyak menerapkan mean, median, modus untuk membantu memecahkan masalah tersebut. Sehingga, penting bagi kita untuk memahami materi ini dengan baik.
Nah, sekian pembahasan terkait mean, median, modus yang mampu membantu permasalahan kamu sehari-hari. Jangan lupa untuk selalu berlatih dengan soal-soal yang ada kamu bisa menjadi lebih jago lagi.