Pertidaksamaan Linear Satu Variabel (PtLSV)

Pertidaksamaan Linear Satu Variabel- Pertidaksamaan linear satu variabel merupakan suatu kalimat terbuka yang hanya mempunyai satu variabel dan berderajat satu serta memuat hubungan (<,> >  atau < ).

Sebagai contohnya, lihat beberapa kalimat seperti di bawah ini:

1. X > 9
2. 3x – 3 < 8
3. 3b > b + 6
4. 5n – 3 < 3n + 2

Beberapa kalimat terbuka di atas menggunakan tanda hubung seperti <, >, > atau <. Yang menandakan kalimat tersebut merupakan  pertidaksamaan.

Masing-masing pertidaksamaan itu hanya memiliki satu variabel, yakni x, a dan n. Pertidaksamaan tersebut disebut sebagai pertidaksamaan satu variabel. Peubah (variabel) pertidaksamaan di atas berpangkat satu atau juga disebut sebagai berderajat satu menjadi dinamakan pertidaksamaan linear.

Pertidaksamaan linear satu variabel merupakan kalimat terbuka yang hanya mempunyai satu variabel dan berderajat satu serta terdapat hubungan (<, >, ³atau £ ).

Bentuk umum dari PtLSV dalam variabel dapat dinyatakan seperti di bawah ini:

ax + b < 0, ax + b > 0, atau ax + b > 0, atau ax + b < 0,dengan a < 0, a serta b merupakan bilangan nyata (real).

Dibawah ini terdapat beberapa contoh dari PtLSV dengan menggunakan variabel x, antara laing:

1. 3x – 2 < 0
2. 3x – 2 < 0
3. 5x – 1 > 8
4. 3x + 1 > 2x – 4
5. 10 < 2(x + 1)

Sifat Pertidaksamaan Linear Satu Variabel

Sama halnya dengan yang ada dalam persamaan linear satu variabel, dalam mencari penyelesaian pertidaksamaan linear satu variabel bisa dilakukan dengan menggunakan cara subtitusi.

Namun, kalian juga dapat melakukannya dengan cara mengurangkan, menjumlahkan, mengkali, ataupun membagi kedua ruas pertidaksamaan dengan bilangan yang sama.

Pertidaksamaan dalam matematika merupakan kalimat atau pernyataan matematika yang menunjukkan perbandingan ukuran dua objek atau lebih.

Seperti yang ada pada A < B pertidaksamaan linear satu variabel x dan C merupakan konstanta tidak nol.

Pertidaksamaan A < B ekuivalen dengan:

1. A + C < B + C
2. A – C < B – C
3. A x C < B x C, bila C > 0 untuk seluruh x
4. A x C > B x C, bila C < 0 untuk seluruh x
5. A/C < B/C, bila C > 0 untuk seluruh x
6. A/C > B/C, bila C < 0 untuk seluruh x

Perlu kalian catat, beberapa sifat di atas juga berlaku untuk  lambang “>” atau “<”.

Contoh Soal PtLSV dan Cara Penyelesaiannya

Di bawah ini akan kami berikan contoh soal sekaligus cara penyeleaiannya dan juga jawaban dari soal pertidaksamaan linear satu variabel. Berikut ulasan selengkapnya.

1. Penjumlahan dan Pengurangan Pertidaksamaan Linear Satu Variabel (PtLSV)

Silakan perhatikan pertidaksamaan yang ada di bawah ini:

x + 3 < 8, dengan x variabel dari bilangan bulat.

Untuk:

x = 1, jadi 1 + 3 < 8, bernilai benar
x = 2, jadi 2 + 3 < 8, bernilai benar
x = 3, jadi 3 + 3 < 8, bernilai benar
x = 4, jadi 4 + 3 < 8, bernilai salah

Pengganti x merupakan 1,2, dan 3 sehingga pertidaksamaan x + 3 < 8 merupakan benar dinamakan penyelesaian dari pertidaksamaan tersebut.

2. Perkalian atau pembagian Pertidaksamaan Linear Satu Variabel (PtLSV)

Perhatikan pertidaksamaan dibawah ini:

Untuk bilangan x asli kurang dari 10 maka penyelesaiannya yakni x = 7, x = 8, atau x = 9

Berdasarkan uraian di atas, bisa kita tarik kesimpulan bahwa:

 “Setiap pertidaksamaan tetap ekuivalen, dengan tanda ketidaksamaan tidak berubah, walaupun kedua ruas dikalikan dengan bilangan positif yang sama”

Contoh Soal:

Saat ini perhatikan pertidaksamaan berikut ini:

a. –x > – 5, dengan x adalah bilangan asli kurang dari 8. Pengganti x yang memenuhi yaitu x = 1, x = 2, x = 3 atau x = 4.

Cara lain untuk menyelesaikan soal pertidaksamaan di atas yakni dengan cara mengalikan kedua ruasnya dengan bilangan negatif yang sama.

* –x > –5

–1(–x) > – 1(–5), (kedua ruas dikalikan dengan –1 dan tanda pertidaksamaan tetap)

x > 5

Penyelesaiannya yaitu dengan x = 6 atau x = 7.

* –x > –5

–1(–x) < –1(–5), (kedua ruas dikalikan dengan –1 serta tanda pertidaksamaan berubah dari > menjadi <)

x < 5

Penyelesaiannya yakni x = 1, x = 2, x = 3, atau x = 4.

Berdasarkan penyelesaian tersebut ternyata, pertidaksamaan yang mempunyai penyelesaian sama adalah:

–x > –5 dan –1(–x) < –1(–5)

sehingga, –x > –5 <=> –1(–x) < –1(–5)

b. –4x <–8, dengan x bilangan asli kurang dari 4. Pengganti x yang memenuhi yaitu x = 2, atau x = 3. sehingga, penyelesaiannya yakni x = 2 atau x = 3.

Berdasarkan penjelasan di atas maka dapat kita tarik kesimpulan bahwa:

“Suatu pertidaksamaan apabila kedua ruasnya dikalikan dengan bilangan negatif yang sama maka tanda pertidaksamaan berubah”

Contoh:

3. Soal cerita 

Soal certa 1.

Jumlah dua bilangan tidak lebih dari 120. Apabila bilangan kedua merupakan 10 lebihnya dari bilangan pertama, maka tentukan batas nilai untuk bilangan pertama.

Jawab:

Dari soal di atas, dapat kita ketahui bahwa terdapat dua besaran yang tidak diketahui. Yakni bilangan pertama dan juga bilangan kedua.

Maka berikutnya kita akan jadikan kedua besaran tersebut sebagai suatu variabel.

Sebagai contoh:

Dari soal tersebut juga kita ketahui bahwasannya bilangan kedua “10 lebihnya dari bilangan pertama”, maka akan berlaku hubungan seperti berikut:

y = x + 10

Dalam soal juga diketahui bahwa jumlah kedua bilangan “tidak lebih” dari 120.

Kalimat “tidak lebih” adalah tanda indikasi pertidaksamaan kurang dari sama dangan (≤). Sehingga, bentuk pertidaksamaan yang sesuai dengan soal yaitu pertidaksamaan kurang dari sama dengan.

Kemudian kita susun pertidaksamaannya seperti:

Sehinga, batas nilai untuk bilangan pertama tidak lebih dari 55.

Soal cerita 2.

• Tentukan model matematikan dari persamaan panjang kawat yang dibutuhkan dalam x.
• Apabila panjang kawat yang diapakai semuanya tidak lebih dari 132 cm, maka tentukan ukuran dari nilai maksimum dari balok tersebut.

Jawab:

Supaya kita lebih mudah untuk memahami soal di atas, maka perhatikan ilustrasi balok di bawah ini:

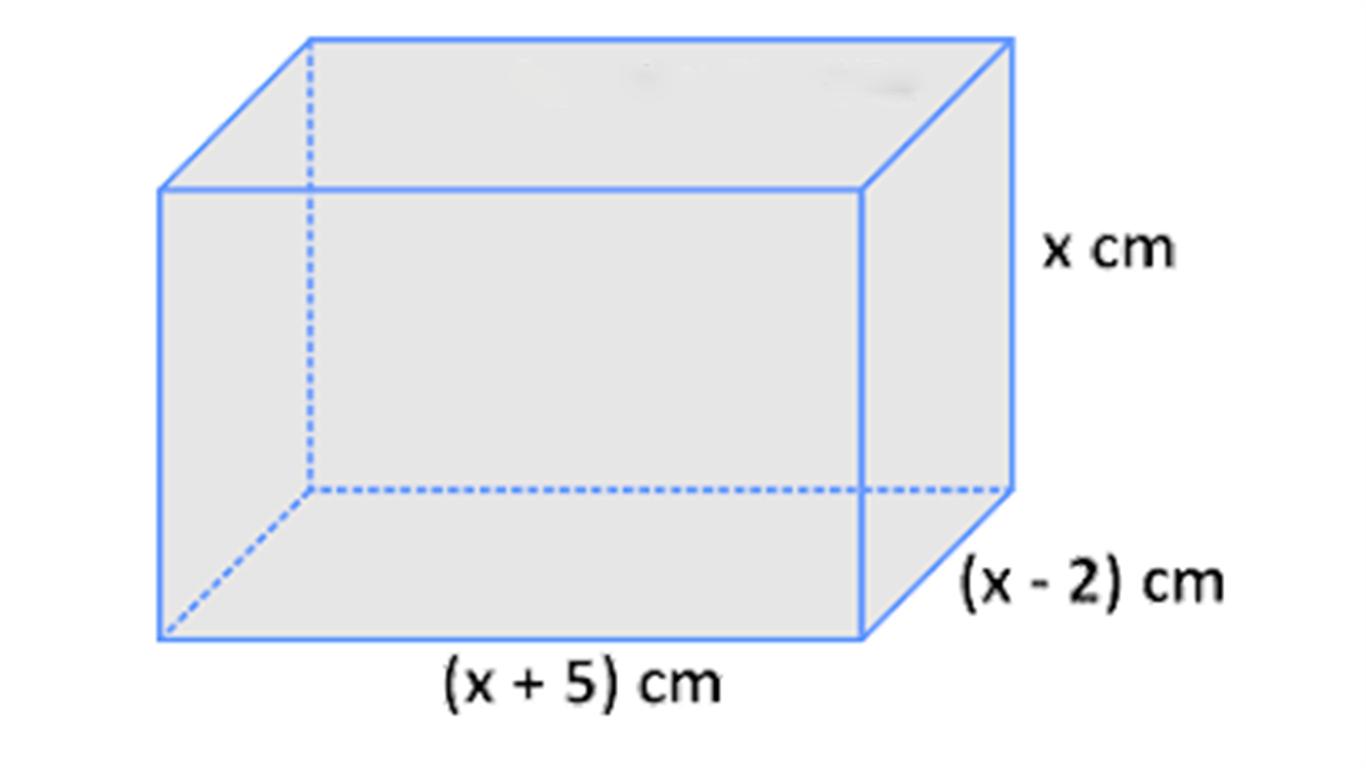
• Menentukan model matematika dari soal di atas.

Contohnya K menyatakan total dari panjang kawat yang diperlukan untuk membuat kerangka balok, maka total panjang kawat yang diperlukan merupakan jumlah dari keseluruhan rusuknya.

Maka, panjang K ialah sebagai berikut.

K = 4p (panjang) + 4l (lebar) + 4t (tinggi)

K = 4(x + 5) + 4(x – 2) + 4x

K = 4x + 20 + 4x – 8 + 4x

K = 12x + 12

Sehingga, kita dapatkan model matematika dari soal cerita nomor dua untuk panjang kawat total yakni K = 12x + 12.

• Menentukan ukuran maksimum balok dari soal di atas.

Panjang kawat tidak boleh melebihi panjang dari 132 cm maka model pertidaksamaannya bisa kita tulis sebagai berikut:

K ≤ 132

12x + 12 ≤ 132

Kemudian kita selesaikan pertidaksamaan linear satu variabel tersebut dengan menggunakan penyelesaian seperti berikuti ini:

12x + 12 ≤ 132

⇒ 12x ≤ 132 – 12

⇒ 12x ≤ 120

⇒ x ≤ 10

Dari penyelesaian x ≤ 10, maka nilai maksimum dari x yaitu 10. Dengan demikian, ukuran balok yakni untuk panjang, lebar dan juga tingginya ialah sebagai berikut:

Panjang = x + 5 ⇔ 10 + 5 = 15 cm

Lebar = x – 2 ⇔ 10 – 2 = 8 cm

Tinggi = x ⇔ 10 cm

Sehinaa kita dapatkan maksimum untuk balok tersebut adalah (15 × 8 × 10) cm.

Soal cerita 3.

Terdapat jumlah dari dua bilangan kurang dari 80. Bilangan kedua sama dengan tiga kali dari bilangan pertama.

Tentukan batas-batas dari kedua bilangan tersebut.

Jawab:

Andaikan bilangan pertama kita sebut sebagai x, maka bilangan kedua sama dengan 3x.

Jumlah kedua bilangan tersebut kurang dari 80. Oleh sebab itu, model matematikanya ialah seperti berikut ini:

x + 3x < 80 ⇔ 4x < 80

Penyelesaian model matematika ini yaitu 4x < 80 ⇔ x < 20.

Oleh sebab itu, batas bilangan pertama tidak lebih dari 20, sementara bilangan kedua tidak lebih dari 60.

Soal cerita 4.

Permukaan suatu meja yang berbentuk persegi panjang memiliki ukuran panjang 16x cm dan lebar 10x cm.

Apabila luasnya tidak kurang dari 40 dm2, maka tentukan ukuran minimum dari permukaan meja tersebut.

Jawab:

Diketahui panjang permukaan meja yaitu:

• (p) = 16x
• lebar (l) = 10 x
• luas = L.

Model matematika dari luas persegi panjang tersebut ialah sebagai berikut:

L = p × l

L = 16x × 10x

L = 160x2

Dari soal tersebut disebutkan bahwa luas tidak kurang dari 40 dm2 = 4.000 cm2 sehingga pertidaksamaannya bisa kita tulis seperti berikut ini:

L = 160x2 ≥ 4.000

160x2 ≥ 4.000

Kemudian kita selesaikan pertidaksamaan tersebut, dengan penyelesaian sebagai berikut:

160x2 ≥ 4.000

⇒ x2 ≥ 25

⇒ x ≥ ±5

Sebab ukuran besaran tidak boleh negatif, maka nilai minimum untuk x = 5 cm, sehingga kita dapatkan:

p = 16x cm = 16(5) cm = 80 cm

l = 10x cm = 10(5) cm = 50 cm

Sehingga, ukuran minimum dari permukaan meja tersebut yaitu (80 × 50) cm.

Soal cerita 5.

Suatu sepeda melaju di jalan raya dengan persamaan lintasan s(t) = t2 – 10t + 39.

Apabila x dalam meter dan t dalam detik, maka tentukan interval waktu supaya sepeda tersebut sudah menempuh jarak sekurang-kurangnya 15 meter.

Jawab:

Sepeda tersebut bisa menempuh jarak sekurang-kurangnya 15 meter, yang berarti s(t) ≥ 15.

Sehingga, model matematikanya yakni t2 – 10t + 39 ≥ 15. Model ini bisa kita selesaikan dengan cara seperti berikut ini:

t2 – 10t + 39 ≥ 15

⇒ t2 – 10t + 39 – 15 ≥ 0

⇒ t2 – 10t + 24 ≥ 0

⇒ (t – 6)(t – 4) ≥ 0

⇒ t ≤ 4 atau t ≥ 6

Dengan demikian, interval waktu supaya sepeda tersebut sudah menempuh jarak sekurang-kurangnya 15 meter yaitu t ≤ 4 detik atau t ≥ 6 detik.

Soal cerita 6.

Pak Irvan mempunyau sebuah mobil box pengangkut barang dengan daya angkut tidak lebih dari 500 kg.

Berat pak Irvan yaitu 60 kg serta dia akan mengangkut kotak barang yang setiap kotak beratnya 20 kg. Maka:

• Tentukan banyak kotak maksimum yang bisa diangkut oleh pak Irvan dalam sekali pengangkutan!
• Apabila pak Irvan akan mengangkut 115 kota, paling sedikit berapa kali kotak itu akan dapat terangkut semua?

Jawab:

Dari soal kita dapatkan beberapa model matematika seperti berikut:

1. Contohnya x menyatakan banyak kota yang bisa diangkut oleh mobil untuk sekali jalan.
2. Setiap kotak beratnya 20 kg, maka x kotak beratnya 20x kg.
3. Total berat sekali jalan yaitu berat kotak ditambah dengan berat pak Irvan yakni 20x + 60.
4. Daya angkut mobil tidak lebih dari, maka kita menggunakan tanda “≤”.
5. Daya angkut tidak lebih dari 500 kg sehingga dari ketentuan (3) kita dapatkan model pertidaksamaan berikut=
   20x + 60 ≤ 500

• Menentukan banyak kotak maksimum yang bisa diangkut dalam sekali jalan.

Menentukan banyak kotak berarti sama saja dengan menentukan nilai x, yakni dengan menyelesaikan pertidaksamaan di bawah ini:

20x + 60 ≤ 500

⇒ 20x ≤ 500 – 60

⇒ 20x ≤ 440

⇒ x ≤ 22

Dari penyelesaian tersebut, kita dapatkan nilai maksimum dari x yaitu 22. Dengan demikian, dalam setiap kali jalan mobil box dapat mengangkut paling banyak 22 kotak.