Polinomial atau yang biasa disebut juga sebagai Suku banyak adalah sebuah bentuk dari suku-suku dengan nilai banyak yang disusun dari perubah variabel serta konstanta. Operasi yang dipakai hanya penjumlahan, pengurangan, perkalian serta pangkat bilangan bulat tidak negatif.
Adapun bentuk umum dari Polinomial ini, yaitu:
Bentuk Umum Polinomial: an xn + an-1 xn-1 + . . . + a1 x + a
Keterangan:
Dengan an , an-1 , …. , a1 , a0 € R koefisien atau konstanta
Polinom an ≠ 0 , serta n adalah bilangan bulat positif.
Pangkat tertinggi dari x merupakan derajat polinomial. Sementara suku yang tidak mengandung variable (a) disebut sebagai suku tetap (konstan).
Suatu polinomial dapat terlihat seperti berikut:
25x2 + 19x – 06
Contoh lain dari bentuk polinomial yaitu:
- 3x
- x – 2
- -6y2 – (½)x
- 3xyz + 3xy2z – 0.1xz – 200y + 0.5
- 512v5+ 99w5
- 5 (Konstanta adalah koefisien yang variabelnya memiliki pangkat 0, sehingga angka adalah polinomial.)
Suatu polinomial dapat mempunyai:
- Variabel (adalah nilai yang bisa berubah, seperti x, y, z dalam suatu persamaan; boleh mempunyai lebih dari 1 variabel)
- Koefisien (adalah konstanta yang mendampingi variabel)
- Konstanta (suatu nilai tetap serta tidak berubah)
- Eksponen atau pangkat adalah pangkat dari variabel; bisa juga disebut sebagai derajat dari suatu polinomial.
Daftar Isi
Syarat Polinomial
Terdapat juga beberapa syarat sehingga sebuah persamaan bisa disebut sebagai ‘polinomial’, diantaranya ialah sebagai berikut:
- Variabel tidak boleh mempunyai pangkat pecahan atau negatif.
- Variabel tidak boleh masuk dalam sebuah persamaan trigonometri.
Polinomial dan Bukan Polinomial
Berikut adalah beberapa bentuk yang tidak termasuk ke dalam bentuk polinomial, diantaranya ialah sebagai berikut:
- 3xy-2 sebab pangkatnya negatif. Eksponen atau pangkat hanya boleh {0,1,2…}.
- 2/(x+2) sebab membagi dengan variabel tidak diperkenankan (pangkat penyebut yaitu negatif).
- 1/x sebab alasan yang sama ^.
- √x sebab akar merupakan pangkat pecahan, yang tidak diperkenankan.
- x cos x sebab terdapat variabel x dalam fungsi trigonometri
Berikut adalah hal yang diperbolehkan atau termasuk dalam bentuk polinomial, perhatikan baik-baik:
- x/2 dibolehkan, sebab boleh membagi dengan konstanta.
- √x2 boleh, sebab sesudag dijabarkan hasilnya tidak terdapat pangkat pecahan.
- √2 boleh sebab yang diakar merupakan konstanta, bukan variabel.
- ½ x5 – (cos∏)x3 – (tan 60°)x – 1 boleh sebab fungsi trigonometri merupakan konstanta, serta tidak terdapat variabel di dalamnya

bentuk di atas boleh, sebab sesudah dijabarkan akan menjadi:

di mana tidak terdapat variabel sebagai penyebut atau variabel berpangkat negatif
Nilai Polinomial
Nilai polinomial f(x) untuk x=k atau f(k) dapat kita cari dengan menggunakan metode substitusi atau dengan skema Horner. Berikut rinciannya:
Cara subtitusi:
Dengan mensubtitusikan x = k ke dalam polinomial, sehingga akan menjadi:
f(x) = an kn + an-1 kn-1 + . . . + a1 k + a
Cara skema horner:
Sebagai contoh:
(f(k) = x3 + bx2 + cx + d sehingga: f(k) = ak3 + bk2 + ck + d
xa3 + bx2 + cx + d = (ak2 + bk + c)k+d
= ((ak + b)k + c)k+d
Pembagian Polinomial
Secara umum, pembagian dalam polinomial dapat dituliskan seperti di bawah ini:
Rumus: f(x) = g(x) h(x) + s(x)
Keterangan:
- f(x) merupakan suku banyak yang dibagi.
- g(x) merupakan suku banyak pembagi.
- h(x) merupakan suku banyak hasil bagi.
- s (x) merupakan suku banyak sisa.
Pembagian Polinomial Dengan Cara Horner
Pembagian suku banyak atau polinomial f(x) oleh (x-k) bisa kita lakukan dengan menggunakan cara atau metode horner.
Cara ini bisa kita pakai untuk pembagi berderajat 1 atau pembagi yang bisa difaktorkan menjadi pembagi-pembagi berderajat 1.
Caranya ialah seabgai berikut:
- Tulis koefisiennya saja → harus runtut atau urut mulai dari koefisien xn, xn – 1, … sampai konstanta (apabila terdapat variabel yang tidak ada, maka koefisiennya ditulis 0)
Sebagai contoh: untuk 4x3 – 1, koefisien-koefisiennya yaitu 4, 0, 0, dan -1 (untuk x3, x2, x, dan konstanta)
- Apabila koefisien derajat tertinggi P(x) ≠ 1, maka hasil baginya harus kita bagi kembali dengan koefisien derajat tertinggi P(x).
- Apabila pembagi bisa kita difaktorkan, maka:
- Apabila pembagi bisa difaktorkan menjadi P1 serta P2, maka S(x) = P1.S2 + S1
- Apabila pembagi bisa difaktorkan menjadi P1, P2, P3, maka S(x) = P1.P2.S3 + P1.S2 + S1
- Apabila pembagi dapat difaktorkan menjadi P1, P2, P3, P4, maka S(x) = P1.P2.P3.S4 + P1.P2.S3 + P1.S2 + S1
- dan begitu juga seterusnya.
Contoh soal menggunakan cara horner:
Soal 1.
F(x) = 2x3 – 3x2 + x + 5 dibagi dengan P(x) = 2x2 – x – 1
Jawab:
P(x) = 2x2 – x – 1 = (2x + 1)(x – 1)
P1: 2x + 1 = 0 → x = –½
P2: x – 1 = 0 → x = 1
Cara Hornernya:
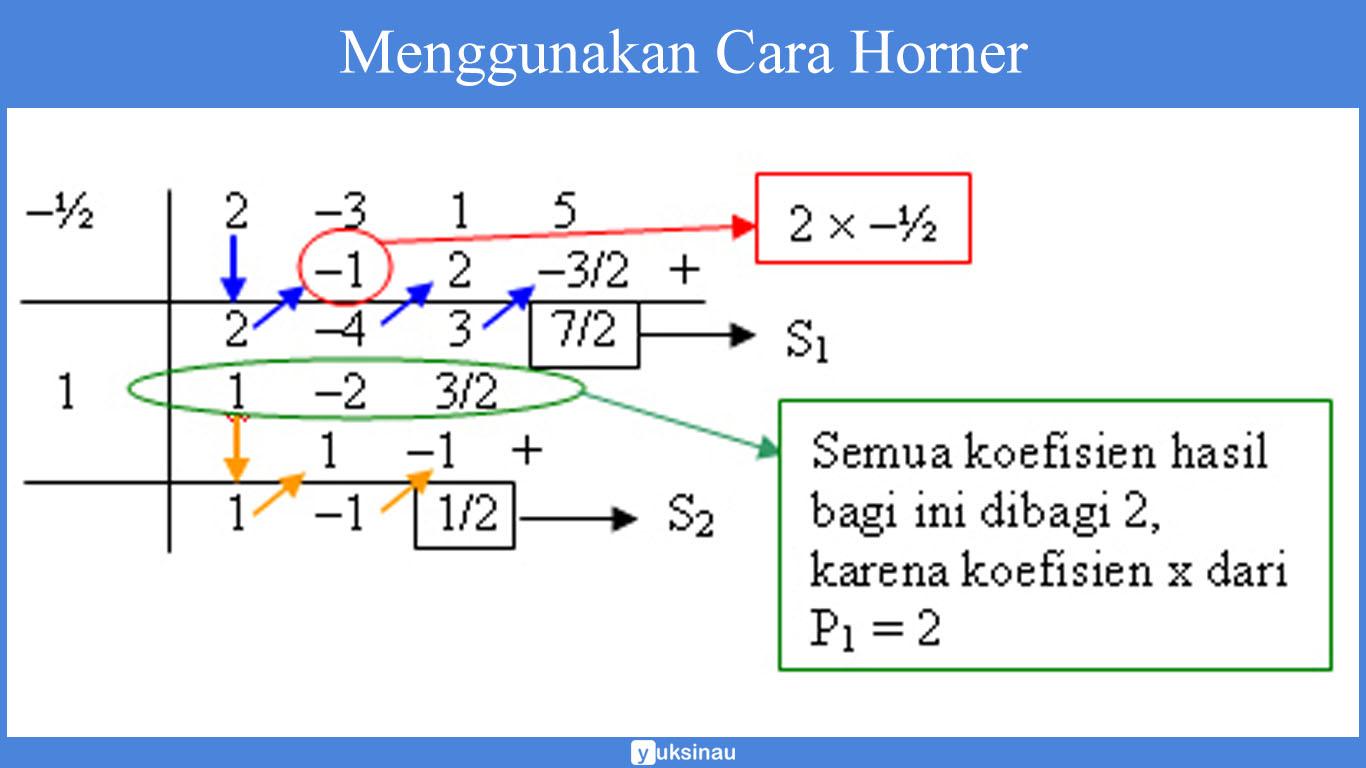
H(x) = 1.x – 1 = x – 1
S(x) = P1.S2 + S1 = (2x + 1).1/2 + 7/2 = x + ½ + 7/2 = x + 4
Koefisien Tak Tentu
F(x) = P(x).H(x) + S(x)
Untuk contoh soal di atas (soal no 1 pada cara horner), sebab F(x) berderajat 3 serta P(x) berderajat 2, maka dari itu:
H(x) berderajat 3 – 2 = 1
S(x) berderajat 2 – 1 = 1
Sehingga, misalnya H(x) = ax + b dan S(x) = cx + d
Maka:
2x3 – 3x2 + x + 5 = (2x2 – x – 1).(ax + b) + (cx + d)
Ruas kanan menjadi:
= 2ax3 + 2bx2 – ax2 – bx – ax – b + cx + d
= 2ax3 + (2b – a)x2 + (–b – a + c)x + (–b + d)
Samakan koefisien ruas kiri dan juga ruas kanan, sehingga menjadi:
x3 → 2 = 2a → a = 2/2 = 1
x2 → –3 = 2b – a → 2b = –3 + a = –3 + 1 = –2 → b = –2/2 = –1
x → 1 = –b – a + c → c = 1 + b + a = 1 – 1 + 1 → c = 1
Konstanta → 5 = –b + d → d = 5 + b = 5 – 1 → d = 4
Sehingga hasil akhirnya adalah:
H(x) = ax + b = 1.x – 1 = x – 1
S(x) = cx + d = 1.x + 4 = x + 4
Rumus patokan yang harus kalian ketahui adalah:
- Derajat H(x) = Derajat F(x) – Derajat P(x)
- Derajat S(x) = Derajat P(x) – 1
Penjumlahan, Pengurangan dan Perkalian Polinomial
Berikut ini akan kami berikan contoh soal polinomial pada opersai penjumlahan, pengurangan, dan juga pengurangan. Perhatikan baik-baik ya!!
Contoh soal:
Diketahui suku banyak f(x) serta g(x) adalah sebagai berikut:
- f(x) = 2x3 – x2 + 5x – 10
- g(x) = 3x2 – 2x + 8
Maka tentukanlah:
a) f(x) + g(x)
b) f(x) – g(x)
c) f(x) x g(x)
Jawab:
a) f(x) + g(x) = (2x3 – x2 + 5x – 10) + (3x2 – 2x + 8)
= 2x3 – x2 + 3x2 + 5x – 2x – 10 + 8
= 2x3 + 2x2 + 3x – 2
b) f(x) – g(x) = (2x3 – x2 + 5x – 10) – (3x2 – 2x + 8)
= 2x3 – x2 – 3x2 + 5x + 2x – 10 – 8
= 2x3 – 4x2 + 7x – 18
c) f(x) x g(x) = (2x3 – x2 + 5x – 10) × (3x2 – 2x + 8)
= 2x3(3x2 – 2x + 8) – x2(3x2 – 2x + 8) + 5x(3x2 – 2x + 8) – 10(3x2 – 2x + 8)
= 2x5 – 4x4 + 16x3 – 3x4 + 2x3 – 8x2 + 15x3 – 10x2 + 40x – 30x2 + 20x – 80
= 2x5 – 7x4 + 33x3 – 48x2 + 60x – 80
Bagaimana? Mudah bukan?
Teorema
Teorema ini digunakan untuk menentukan akar persamaan dari pangkat lebih dari dua. Teorema terbagi menjadi dua macam, yakni teorema sisa dan teorema faktor. Berikut penjelasannya.
Teorema Sisa
Misalnya f(x) dibagi dengan p(x) dengan hasil bagi h(x) serta sisa h(x), maka akan kita dapatkan hubungan:
f(x) = P(x) x H(x) x S(x)
Apabila f(x) berderajat n serta P(x) pembagi berderajat m, dengan m ≤ n , maka:
- H(x) berderajat (n – m)
- S(x) berderajat maksimum (m – 1)
Teorema untuk sisa ialah sebagai berikut:
- Apabila f(x) berderajat n dibagi dengan (x -k) maka sisanya adaah S = f(k). Sisa dari f(k) yaitu nilai suku banyak untuk x = k.
- Apabila f(x) berderajat n dibagi dengan (ax + b) maka sisanya adalah S = f (-b/a). Sisa dari f (-b/a) merupakan nilai untuk x = -b/a.
- Pembagi berderajat m ≥ 2 yang bisa difaktorkan maka sisa berderajatnya adalah (m – 1).
Adapun rumus sisa yang biasa digunakan, yaitu:
s(x) = mx + n
Untuk lebih memahami uraian di atas, berikut akan kami berikan contoh soalnya:
Cohtoh soal
Soal 1.
Suatu suku banyak apabila dibagi oleh x + 2 bersisa -13 serta apabila dibagi x – 3 sisanya 7. Tentukan sisanya apabila suku banyak tersebut dibagi x2 – x – 6!
Jawab:
Cara 1:
Rumus Sisa yaitu: s(x) = mx + n, sehingga:
k(x) = x2 – x – 6
k(x) = (x + 2) (x – 3)
Kita ketahui jika dibagi oleh x + 2 maka akan bersisa -13 serta apabila dibagi x – 3 sisanya akan menjadi 7
Maka dari itu, k(-2) = -13 dan k(3) = 7
Sehingga, kembalikan ke rumus Sisa, menjadi:
s(x) = mx + n
s(-2) = -2m + n = -13
s(3) = 3m + n = 7
Kemudian kita pakai metode eliminasi, caranya:
-2m + n = -13
3m + n = 7
-5m = -20
m = 4
Kemudian menggunakan metode substitusi, substitusikan ke persamaan:
12 + n = 7
n = -5
Kemudian kembalikan ke rumus s(x) = mx + n
Sehingga diketahui Sisa Polinomial jika dibagi x2 – x – 6 hasil nya 4x – 5.
Uraian singkat dari soal:
Polinominal 8x3 – 2x + 5 dibagi dengan x + 2 mempunyai sisa (S) berikut:
S = f(k) = 8x3 – 2x + 5
S = f(-2) = 8(-2)3 – 2(-2)2 + 5
S = -67
Teorema Faktor
Sebuah suku banyak F(x) memiliki faktor (x – k) apabila F(k) = 0 (sisanya apabila dibagi dengan (x – k) hasilnya 0)
Catatan: apabila (x – k) merupakan faktor dari F(x) maka k disebut sebagai akar dari F(x)
Tips
- Untuk mencari akar dari sebuah suku banyak dengan cara Horner, bisa kita gunakan dengan cara mencoba-coba dengan angka dari faktor-faktor konstanta dibagi faktor-faktor koefisien pangkat tertinggi yang akan nantinya akan memberikan sisa = 0.
Sebagai contoh:
Untuk x3 – 2x2 – x + 2 = 0, faktor-faktor konstantanya adalah: ±1, ±2. Faktor-faktor koefisien pangkat tertinggi adalah: ±1.
Sehingga, angka-angka yang perlu untuk dicoba yaitu: ±1 dan ±2 untuk 4x3 – 2x2 – x + 2 = 0.
Faktor-faktor konstantanya: ±1, ±2, faktor-faktor koefisien pangkat tertinggi: ±1, ±2, ±4.
Sehingga, angka-angka yang perlu dicoba: ±1, ±2, ±1/2, ±1/4 - Apabila jumlah koefisien suku banyak = 0, maka pasti salah satu akarnya merupakan x = 1.
- Apabila jumlah koefisien suku di posisi genap = jumlah koefisien suku di posisi ganjil, maka pasti salah satu akarnya merupakan x = –1.
Perhatikan contoh soal di bawah ini:
Tentukan penyelesaian dari x3 – 2x2 – x + 2 = 0?
Jawab:
Faktor-faktor dari konstantanya adalah 2, merupakan ±1 serta ±2 dan faktor-faktor koefisien pangkat tertingginya, adalah 1, merupakan ±1, sehingga angka-angka yang perlu dicoba: ±1 dan ±2
Sebab jumlah semua koefisien + konstantanya = 0 (1 – 2 – 1 + 2 = 0), maka, pasti x = 1 merupakan salah satu faktornya, sehingga:
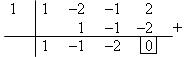
Sehingga, x3 – 2x2 – x + 2 = (x – 1)(x2 – x – 2)
= (x – 1)(x – 2)(x + 1)
x = 1 x = 2 x = –1
Maka dari itu, dapat kita ketahui himpunan penyelesaiannya: {–1, 1, 2}.
Sifat Akar Akar Suku Banyak
Pada persamaan berderajat 3:
ax3 + bx2 + cx + d = 0 akan memiliki akar-akar x1, x2, x3
Dengan sifat-sifat:
- Jumlah 1 akar: x1 + x2 + x3 = – b/a
- Jumlah 2 akar: x1.x2 + x1.x3 + x2.x3 = c/a
- Hasil kali 3 akar: x1.x2.x3 = – d/a
Pada persamaan berderajat 4:
ax4 + bx3 + cx2 + dx + e = 0 akan memiliki akar-akar x1, x2, x3, x4
Dengan sifat-sifat:
- Jumlah 1 akar: x1 + x2 + x3 + x4 = – b/a
- Jumlah 2 akar: x1.x2 + x1.x3 + x1.x4 + x2.x3 + x2.x4 + x3.x4 = c/a
- Jumlah 3 akar: x1.x2.x3 + x1.x2.x4 + x2.x3.x4 = – d/a
- Hasil kali 4 akar: x1.x2.x3.x4 = e/a
Pada persamaan berderajat 5:
ax5 + bx4 + cx3 + dx + e = 0 akan mempunyai akar-akar x1, x2, x3, x4, x5
Dengan sifat-sifat:
- Jumlah 1 akar: x1 + x2 + x3 + x4 + x5 = – b/a
- Jumlah 2 akar: x1.x2 + x1.x3 + x1.x4 + x2.x3 + x2.x4 + x3.x4 + x4.x5 =c/a
- Jumlah 3 akar: x1.x2.x3 + x1.x2.x4 + x2.x4.x5 = – d/a
- Hasil kali 4 akar: x1.x2.x3.x4.x5 = e/a
Dari kedua persamaan tersebut, kita bisa menurunkan rumus yang sama untuk persamaan berderajat 6 dan begitu juga seterusnya. (Amati pola: –b/a, c/a, –d/a , e/a, …).
Pembagian Istimewa
Perhatikan gambar di bawah ini baik-baik:

Contoh Soal dan Pembahasan
Soal 1.
Polinomial f(x) ÷ (x – 2) sisanya 24 serta f(x) ÷ (x + 5) sisanya 10. Maka f(x) tersebut dibagi x2 + 3x – 10 sisanya yaitu…
a. x + 34
b. x – 34
c. x + 10
d. 2x + 20
e. 2x – 20
Jawab:
Rumusnya yaitu P(x) = H(x) . Pembagi + (px + q)
Diketahui:
- f(x) ÷ (x – 2) sisa 24, maka:
f(x) = H(x)(x – 2) + 24
Kemudian subtitusikan x = 2, sehingga:
f(2) = H(2)(2 – 2) + (2p + q)
= 2p + q = 24 …. (i)
f(x) ÷(x + 5) sisa 10, sehingga:
f(x) = H(x)(x + 5) + 10
Dengan Subtitusikan x = -5, sehingga:
(f(-5) = H(-5)(-5 + 5) + (-p + q)
= -5p + q = 10 …. (ii)
Eliminasikan persamaan (i) serta (ii):
2p +q =24
-5p +q =10
7p = 14
p =2
Dalam mensubtitusikan p = 2 pada 2p + q = 24
2(2) + q = 24
q = 24 – 4
q = 20
Apabila f(x) dibagi x2 + 3x – 10 maka:
f(x) = H(x) (x2 + 3x – 10) + (px + q)
f(x) = H(x) (x-2) (x + 5) + (px + q)
sisa px + q = 2x + 20
Jawaban: D
Soal 2.
Suku banyak x4 – 3x3 – 5x2 + x – 6 dibagi oleh x² – x -2 sisanya sama dengan …
a. 16x + 8
b. 16x – 8
c. -8x + 16
d. -8x – 16
e. -8x – 24
Jawab:
Diketahi pembaginya yaitu: x² – x -2, sehingga:
x² – x -2= 0
(x – 2) (x + 1) = 0
x = 2 dan x = -1
Ingat rumus: P(x) = H(x) + (px + q), sehingga sisanya (px + q), maka:
- x = 2
f(2) = 2p + q
24 – 3(2)3 – 5(2)2 + 2 – 6 = 2p + q
16 – 24 – 20 + 2 – 6 = 2p + q
-32 = 2p + q … (i)
- x = -1
f(-1) = -p + q
(-1) – 3(-1)3 – 5(-1)2 + (-1) – 6 = -p + q
1 + 4 – 5 – 1 – 6 = -p + q
-8 = -p + q …(ii)
Eliminasikan persamaan (i) serta (ii), menjadi:
-32 =2p +q
-8 =-p +q
-24 =3p
p = -8
Jika kita substitusikan p = –p + q = -8
-(-8) + q = -8
q = -16
Maka , sisanya adalah = p + q = -8x – 16
Jawaban: D
Soal 3.
Diketahui g(x) = 2x3 + ax2 + bx + 6 dan h(x) = x2 + x – 6 merupakan faktor dari g(x). Nilai a yang memenuhi yaitu…
a. -3
b. -1
c. 1
d. 2
e. 5
Jawab:
x2 + x – 6 = 0
(x + 3)(x – 2) = 0
x = -3 dan x = 2
Sebab h(x) merupakan faktor dari g(x), sehingga:
- g(-3) = 0
2x3 + ax2 + bx + 6 = 0
2(-3)3 + a(-3)2 + b(-3) + 6 = 0
-54 + 9a – 3b + 6 = 0
9a – 3b = 48 … (i)
- g(2) = 0
2x3 + ax2 + bx + 6 = 0
2(2)3 + a(2)2 + b(2) + 6 = 0
16 + 4a + 2b + 6 = 0
4a + 2b = – 22
2a + b = – 11 … (ii)
Eliminasikan persamaan (i) serta (ii):
- 9a -3b 48 | x1 | 9a -3b =48
- 2a +b =-11 | x3 | 6a +3b =-33
- 15a =15
- a = 1
Jawaban: C
Soal 4.
Apabila f(x) dibagi oleh x2 – 2 dan x2 – 3x masing-masing memiliki sisa 2x + 1 dan 5x + 2 maka f(x) dibagi oleh x2 – 5x + 6 memiliki sisa…
a. 22x – 39
b. 12x + 19
c. 12x – 19
d. -12x + 29
e. -22x + 49
Jawab:
Misalnya sisa pembagiannya S(x) = px+ q, maka:
f(x) dibagi oleh x² – 2x ataupun x(x -2) → x =2 sisanya 2x + 1, sehingga:
S(2) = 2x + 1
S(2) = 2(2) + 1
S(2) = 5
2p + q = 5 … (i)
f(x) dibagi oleh x2 – 3x ataupun x(x – 3) –> x = 3 sisanya 5x + 2, sehingga:
S(3) = 5x + 2
S(3) = 5(3) + 2
S(3) = 17
3p + q = 17 … (ii)
Eliminasikan (i) serta (ii):
2p + q =5
3p +q =17
-p = -12
p = 12
Substitusikan p = 12 dalam 2p + q = 5
2(12) + q = 5
24 + q = 5
q = -19
Maka sisanya adalah: px + q = 12x – 19
Jawaban: C.
Soal 5.
Polinomial 2x3 + 5x2 + ax + b ÷ x + 1 sisa 1 serta apabila ÷ (x – 2) sisanya 43. Nilai a + b = …
a. -4
b. -2
c. 0
d. 2
e. 4
Jawab:
- Dibagi (x + 1) sisanya 1
Sehingga, pada saatu x = -1, h(-1) = 1
2(-1)3 + 5(-1)2 + a(-1) + b = 1
-2 + 5 – a + b = 1
-a + b = 1 – 3
-a + b = -2 …(i)
- Dibagi (x – 2) sisanya 43
Sehingga pada saat x = 2, h(2) = 43
2(2)3 + 5(2)2 + a(2) + b = 43
16 + 20 + 2a + b = 43
2a + b = 43 – 36
2a + b = 7 …. (ii)
Eliminasikan (i) sera (ii):
2a +b =7
-a +b =-2
3a = 9
a =3
Subtitusikan a = 3 ke dalam 2a + b = 7, sehingga menjadi:
2(3) + b = 7
6 + b = 7
b = 1
Sehingga, a + b = 3 + 1 = 4
Jawaban: E
Soal 6.
Salah satu faktor dari (2x³ -5x² – px =3) merupakan (x + 1). Faktor lain dari suku banyak tersebut ialah…
a. (x – 2) dan (x – 3)
b. (x + 2) dan (2x – 1)
c. (x + 3) dan (x + 2)
d. (2x + 1) dan (x – 2)
e. (2x – 1) dan (x – 3)
Jawab:
Yang merupakan faktornya adalah x + 1 –> x = -1
f(-1) = 0
2(-1)³ – 5(-1)³ – p(-1) + 3 = 0
-2 – 5 + p + 3 = 0
p = 4
Maka, f(x) = 2x³ -5x³ – 4x =3
= (x + 1)(2×2 – 7x + 3)
= (x + 1)(2x – 1)(x – 3)
Sehingga, faktor yang lainnya yaitu (2x – 1) dan juga (x – 3).
Jawaban: E
Soal 7.
Ada Dua polinomial x³ -4x³ – 5x + m dan x2 -3x – 2 ÷ x + 1 akan memiliki sisa sama, maka nilai 2m + 5 = …
a. 17
b. 18
c. 24
d. 27
e. 30
Jawab:
Misalnya f(x) = x³ -4x2 – 5x + m dan x2 -3x – 2
Jika ÷(x + 1 ) –> x = -1 akan mempunyai sisa sama, maka:
f(-1) = g(-1)
(-1)³ – 4(-1)2 + 5(-1) + m = (-1)2 + 3(-1) – 2
-1 -4 – 5 + m = 1 – 3 – 2
-10 + m = -4
m = -4 + 10
m = 6
Sehingga, nilai dari 2m + 5 = 2(6) + 5 = 17
Jawaban: A
Soal 8.
Dalam f(x) ÷ (x – 1) sisa 3, sementara ÷ (x – 2) sisa 4. Apabila dibagi dengan x2 -3x + 2 maka sisanya adalah…
a. –x – 2
b. x + 2
c. x – 2
d. 2x + 1
e. 4x – 1
Jawab:
- f(x) dibagi (x – 1) sisanya 3 → f(1) = 3
- f(x) dibagi (x – 2) sisanya 4 → f(1) = 4
Misalkan sisanya = ax + b, maka:
x2 -3x + 2 = (x – 2)(x – 1)
Maka sisanya ialah:
f(1) = 3
a + b = 3 … (i)
f(2) = 4
2a + b = 4 … (ii)
Eliminasikan (i) serta (ii):
2a + b =4
a +b = 3
a =1
Dalam Subtitusi a = 1 pada a + b = 3
1 + b = 3
b = 2
Sehingg diketahui sisanya adalah: ax + b = x + 2
Jawaban: B
Soal 9.
Banyaknya akar-akar real dari x4 – 3x3 – 3x2 + 7x + 6 = 0 adalah …
a. 2
b. 3
c. 4
d. 5
e. 6
Jawab:
x4 -3×3 -3×2 +7x +6 =0
(1 +)(x3 -4×2 +x +6) =0
(x +1)(x+1- x2 – 5x +6) + 0
(x +1)(x +1)(x -2)(x -3) = 0
x = -1, x = 2, dan x = 3
Sehingga banyak akar- akarnya terdapat 3 buah.
Jawaban: B
Soal 10.
polinomia : x3 -4x + px +6 dan z2 +3x -2 dibagi (x + 1) mempunyai sisa yang sama maka nilai p adalah …
a. 7
b. 5
c. 3
d. -5
e. -7
Jawab:
Misalnya f(x) = x3 -4×2 + px +6 serta x2 +3x -2
Kemudian dibagai (x + 1) maka,
x = -1
f(-1) = g(-1)
(-1)3 – 4(-1)2 + p(-1) + 6 = (-1)2 + 3( -1) -2
-1 – 4 – p + 6 = 1 -3 – 2
1 – p = -4
p = 5
Jawaban: B
Demikianlah ulasan singkat terkait Polinomial yang dapat kami sampaikan. Semoga ulasan di atas dapat kalian jadikan sebagai bahan belajar kalian.
2 pemikiran pada “Polinomial”