Prisma Segi Enam: Ciri-Ciri, Rumus, Rusuk Sisi Titik

Dalam pelajaran Matematika, kamu akan menemukan materi mengenai bangun ruang yang lebih kompleks dibanding bangun datar, sebab bangun ruang mempunyai luas alas serta volume. Salah satu bangun ruang adalah prisma segi enam.

Di samping itu, terdapat bangun ruang lain, seperti kubus, balok, limas, tabung, dan sebagainya. Kali ini, kita akan membahas prisma yang memiliki atap dan alas berbentuk segi enam, mulai dari pengertian, ciri-ciri, hingga rumus serta contoh soalnya.

Pengertian Prisma Segi Enam

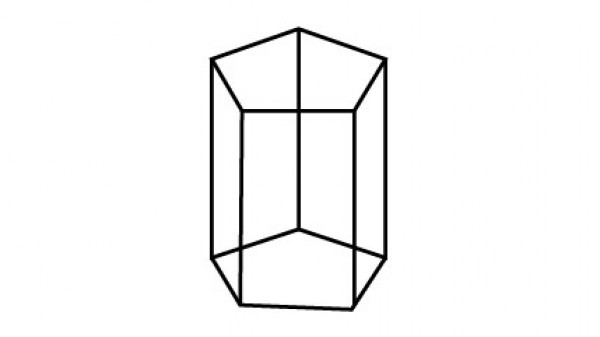
Prisma ini merupakan bangun ruang tiga dimensi yang mempunyai alas dan atap berbentuk segi enam. Prisma ini juga mempunyai selimut dengan bentuk persegi panjang pada sisi sampingnya.

Jenis-Jenis Prisma Segi Enam

Prisma sendiri memiliki ragam-ragam jenis, namun untuk segi enam terdapat dua jenis yang berbeda berdasarkan bentuknya, yakni sebagai berikut.

1. Segi Enam Beraturan

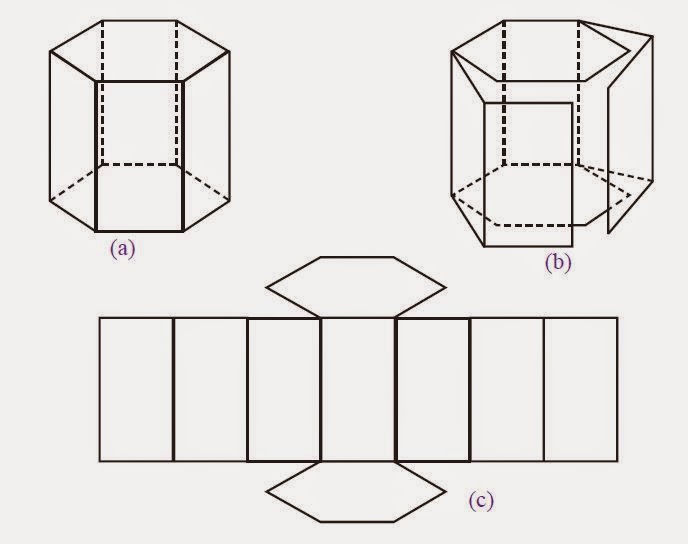
Prisma segi enam beraturan adalah prisma dengan bentuk sisi yang sama panjang serta mempunyai enam sudut yang besarnya sama pula. Hal ini berarti setiap sisi pada prisma memiliki ukuran panjang yang sama persis.

Dari gambar tersebut, kamu dapat melihat bahwa segi enam dapat membentuk enam buah segitiga sama sisi, di mana ketika sudut pusat (360 derajat) dibagi rata menjadi enam, maka besar masing-masing sudut adalah 60 derajat.

2. Segi Enam Tidak Beraturan

Prisma bersegi enam tidak beraturan merupakan prisma dengan dua bentuk sisi yang tidak sama panjang dengan sisi-sisi lain. Hal ini menjadikan sudut-sudut yang terbentuk pada prisma juga tidak sama besar sehingga memiliki cara yang sedikit rumit ketika menghitungnya.

Baca: Bangun Ruang

Ciri-Ciri Prisma Segi Enam

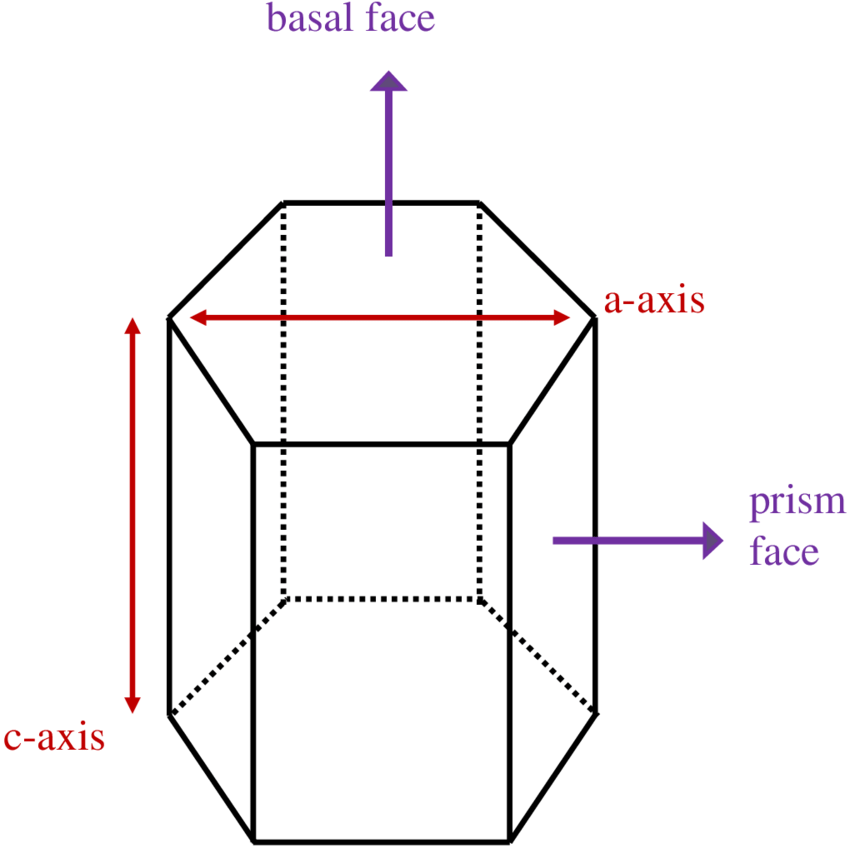
Sifat atau ciri-ciri yang dimiliki oleh prisma ini adalah sebagai berikut.

• Memiliki 18 buah rusuk, di mana 6 buah rusuk adalah rusuk tegak.
• Memiliki 12 titik sudut.
• Memiliki 8 sisi, di mana 6 sisi yang ada di sisi samping adalah sisi yang berbentuk persegi panjang, sementara 2 sisi lain ada di atap dan alas, berbentuk segi enam.

Rusuk Prisma Segi Enam

Unsur prisma bersegi enam yang pertama adalah rusuk. Seperti yang telah dijelaskan sebelumnya, prisma segi enam memiliki 18 buah rusuk, di mana 6 rusuk adalah rusuk tegak. Perhatikan gambar di bawah ini.

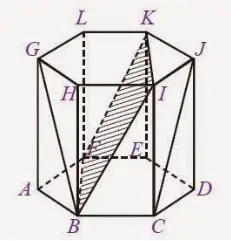
Pada gambar prisma bersegi enam tersebut, yang merupakan rusuk adalah AB, BC, CD, DE, EF, FA, GH, HI, IJ, JK, KL, dan LG. Sementara rusuk tegaknya adalah AG, BH, CI, DJ, EK, dan FL.

Baca: Bangun Ruang Sisi Lengkung

Sisi pada Prisma Segi Enam

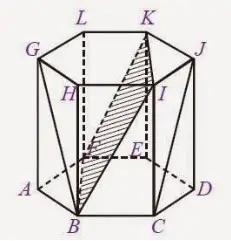
Unsur yang dimiliki segi enam berikutnya adalah sisi. Pada gambar sebelumnya, dapat dilihat bahwa bangun ruang ini memiliki 8 sisi atau bidang, di antaranya adalah sebagai berikut.

• ABCDEF, sebagai sisi alas.
• GHIJK, sebagai sisi atas.
• BCIH, sebagai sisi depan.
• FEKL, sebagai sisi belakang.
• ABHG, sebagai sisi depan kanan.
• AFLG, sebagai sisi belakang kanan.
• CDJI, sebagai sisi depan kiri.
• DEKJ, sebagai sisi belakang kiri.

Pada prisma segi ini juga memiliki diagonal bidang atau diagonal sisi yang berjumlah. Perhatikan kembali gambar di atas, diagonal bidang dari prisma tersebut adalah BG, CJ, BI, AH, HC, ID, DK, JE, KF, LE, LA, GF, HK, IL, BE, dan CF.

Selain itu, pada sebuah prisma segi banyak ada yang disebut bidang diagonal. Menurut gambar yang tertera, empat buah bidang diagonal pada prisma tersebut di antaranya adalah BFKI, ECHL, KLBC, dan HIEF.

Diagonal ruang juga merupakan unsur yang ada pada sebuah prisma dengan segi enam. Berdasarkan gambar tersebut, ada 36 diagonal ruang di sana, dan sembilan di antaranya adalah AI, AJ, AK, BJ, BK, BL, CG, CL, CK, dan lain sebagainya.

Titik Sudut Prisma Segi Enam

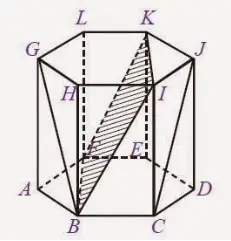
Masih berbicara mengenai unsur prisma bersegi enam, unsur selanjutnya adalah titik sudut. Prisma bentuk ini mempunyai 12 titik sudut. Bila melihat gambar sebelumnya, titik sudutnya adalah A, B, C, D, E, F, G, H, I, J, K, dan L.

Baca: Bangun Ruang Sisi Datar

Rumus Prisma Segi Enam

Bangun ruang tiga dimensi ini dapat dihitung luas permukaan serta volumenya dengan rumus berbeda. Kamu dapat menyimak rumus-rumusnya sebagai berikut.

1. Menghitung Luas Permukaan dan Volume

Untuk dapat mengerjakan soal-soal berkaitan dengan bangun ruang prisma dengan alas segi enam, kamu dapat mempelajari rumus-rumus berikut.

a. Rumus Luas Permukaan Prisma dengan Segi Enam Beraturan

Dapat dihitung dengan rumus sebagai berikut.

L = 2La + Ls

Di mana La adalah luas alas prisma dan Ls adalah selimut.

Untuk segi enam beraturan, rumus luas alas adalah sebagai berikut.

La = 3/2√3 . s²

Di mana s adalah panjang sisi segi enam beraturan.

Untuk segi enam beraturan, rumus luas selimut adalah sebagai berikut.

Ls = Ka . t

Di mana Ka adalah keliling alas dan t adalah tinggi prisma.

b. Rumus Volume Prisma dengan Segi Enam Beraturan

Dapat dihitung dengan rumus sebagai berikut.

V = La . t

Di mana V  adalah volume prisma, La adalah luas alas, dan t adalah tinggi prisma.

2. Contoh Soal

Nah, setelah menguasai rumus-rumusnya, kamu dapat menguji kemampuan dengan beberapa contoh soal. Berikut ini kami sajikan contoh-contoh pengerjaan serta penyelesaiannya.

a. Contoh Soal 1

Sebuah prisma mempunyai alas dengan bentuk segi enam beraturan. Jika panjang sisi alas tersebut adalah 10 cm dan tinggi prisma adalah 7 cm, hitunglah volume prisma tersebut!

Penyelesaian:

b. Contoh Soal 2

Ada sebuah prisma dengan alas segi enam beraturan memiliki volume 576√3 cm^2 dengan tinggi 6 cm. Berapakah panjang sisi segi enam tersebut?

Penyelesaian:

c. Contoh Soal 3

Sebuah prisma mempunyai alas berbentuk segi enam beraturan dengan panjang sisi 15 cm dan tinggi 10 cm. Hitunglah luas permukaan prisma tersebut!

Penyelesaian:

d. Contoh Soal 4

Sebuah prisma dengan alas berbentuk segi enam beraturan memiliki luas permukaan 300 √3 + 480 cm^2 dan panjang sisi segi enam adalah 10 cm. Berapa tinggi prisma tersebut?

Penyelesaian:

Berlatih dengan materi dan pengerjaan soal-soal yang berkaitan dengan prisma segi enam dapat mengasah kemampuan kamu. Walaupun lebih sulit daripada pengerjaan bangun datar, semakin banyak berlatih, semakin terbiasa kamu dalam menyelesaikan persoalan yang lebih banyak lagi.