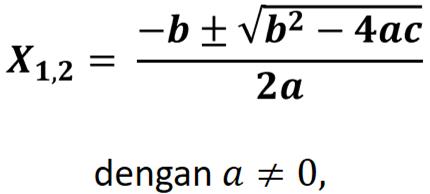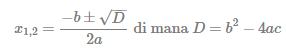Salah satu bab yang dipelajari di dalam matematika ialah persamaan kuadrat atau juga disebut sebagai rumus abc.
Yang mana komponen penyusun rumus satu ini terdiri atas huruf a,b, dan c.
Rumus ABC biasanya dimanfaatkan untuk menyelesaikan permasalahan yang sulit untuk ditemukan sehingga dengan adanya menggunakan rumus satu ini, proses penyelesaian soal akan menjadi lebih mudah untuk dipahami.
Selengkapnya terkait rumus ABC, simak pembahasannya di bawah ini.
Daftar Isi
Pengertian Rumus ABC

Rumus abc merupakan salah satu rumus yang dimanfaatkan untuk mencari akar – akar persamaan kuadrat.
Terdapat beberapa syarat supaya rumus satu ini dapat digunakan, diantaranya yaitu:
- Persamaan kuadrat tersebut memiliki bentuk ax2 + bx + c = 0.
- Nilai nya a ≠ 0.
- Bilangan yang berada di bawah tanda akar di dalam rumus di atas disebut sebagai Diskriminan ( D ), yang mana mana D = b2 − 4ac
- Rumus ABC dapat berlaku apabila nilai D > 0.
Untuk memperoleh rumus ABC, terdapat 3 cara yang dapat kalian gunakan, antara lain:
- Yang pertama ialah memecahkan persamaan kuadrat.
- Yang kedua dengan cara pemfaktoran.
- Dan yang terakhir dengan melengkapi bentuk rumus serta kuadrat.
Formula ABC atau yang biasa disebut sebagai rumus kuadrat satu ini biasanya dimanfaatkan dalam mengarah ke persamaan kuadrat yang sulit untuk ditemukan.
Bahkan beberapa orang lebih suka dengan menggunakan metode satu ini, sebab tanpa dasar pemfaktoran atau mengisi bentuk kuadrat.
Dikatakan sebagai formula abc sebab komponen yang terdapat di dalam formula hanya ada cara a, b, c dan masing – masing variabel tersebut berupa koefisien x2, konstanta, serta koefisien x.
Rumus ABC
Berikut adalah bentuk umum dari rumus ABC, antara lain:
atau
Huruf – huruf a, b, dan juga c pada rumus di atas berperan sebagai koefisien.
Koefisien kuadrat x2 ialah a, koefisien x ialah b, serta c ialah koefisien konstan, pada umumnya disebut juga sebagai konstanta / suku bebas.
Persamaan kuadrat pada dasarnya adalah persamaan matematika yang membentuk suatu geometri lengkung parabola di dalam kuadran xy.
Nilai koefisien yang ada di dalam rumus abc memiliki beberapa arti seperti berikut ini:
- a untuk menentukan cekung atau cembungnya parabila yang dibentuk oleh persamaan kuadrat. Apabila nilai a>0 maka parabola tersebut akan terbuka ke atas.
Tetapi apabila a<0 maka parabola tersebut akan terbuka ke bawah. - b untuk menentukan posisi x puncak parabola, atau sumbu simetri cermin dari kurva yang dibentuk. Posisi tepat sumbu simetri ialah -b/2a dari persamaan kuadrat.
- c untuk menentukan titik potong yang berfungsi sebagai persamaan kuadrat parabola yang dibentuk dengan sumbu y atau ketika nilai x=0.
Contoh Soal
Untuk memudahkan kalian dalam memahami uraian di atas, berikut kami sajikan beberapa soal terkait rumus abc, antara lain:
1. Apabila diketahui suatu persamaan kuadrat x2 + 7x + 10 = 0. Maka tentukan akar – akar persamaannya sehingga nilai x dapat diketahui!
Jawab:
Diketahui persamaan kuadrat a = 1, b = 7, c = 10.
Sehingga dapat disubstitusikan ke dalam rumus persamaan kuadrat sebagai berikut:
x = ( -b ± √b2 – 4ac )/ 2a
x = ( -7 ± √72 – 4.1.(10) )/ 2.1
x = ( -7 ± √49 + 40 )/ 2
x = ( -7 ± √89 )/ 2
x = (-7 + 3)/2
x1 = (-7 – 3)/2 = -5
x2 = (-7 + 3)/2 = -2
Sehingga dapat kita kita ketahui bahwa nilai x1 = -5 serta x2 = -2.
2. Apabila diketahui suatu persamaan kuadrat 2x2 – 5x – 3 = 0. Berapakah nilai x1 dan juga x2 ?
Jawab:
Diketahui persamaan kuadrat a = 2, b = -5, c = -3.
Sehingga dapat disubstitusikan ke dalam rumus persamaan kuadrat sebagai berikut:
x = ( -b ± √b2 – 4ac )/ 2a
x = ( -(-5) ± √(-5)2 – 4.2.(-3) )/ 2.2
x = ( 25 ± √25 + 24 )/ 4
x = ( 25 ± √49 )/ 4
x = (5 + 7)/4
x1 = (5 – 7)/4 = – 1/2
x2 = (5 + 7)/4 = 3
Sehingga dapat kita kita ketahui bahwa nilai x1 = -1/2 dan x2 = 3.
3. Hitunglah nilai x apabila persamaan kuadrat yang diketahui yaitu 3x2 + 7x – 20 = 0!
Jawab:
Diketahui persamaan kuadrat a = 3, b = 7, c = -20.
Sehingga dapat disubstitusikan ke dalam rumus persamaan kuadrat sebagai berikut:
x = ( -b ± √b2 – 4ac )/ 2a
x = ( -7 ± √72 – 4.3.(-20) )/ 2.3
x = ( -7 ± √49 + 240 )/ 6
x = ( -7 ± √289 )/ 6
x = (-7 + 17)/6
x1 = (-7 – 17)/6 = -4
x2 = (-7 + 17)/6 = 5/3
Sehingga dapat kita kita ketahui bahwa nilai x = -4 dan 5/3.
4. Berapakah perkiraan nilai x apabila persamaan kuadrat yang diketahui yaitu x2 – 2x – 3 = 0!
Jawab:
Diketahui persamaan kuadrat a = 1, b = -2, c = -3.
Sehingga dapat disubstitusikan ke dalam rumus persamaan kuadrat sebagai berikut:
x = ( -b ± √b2 – 4ac )/ 2a
x = ( -(-2) ± √(-2)2 – 4.1.(-3) )/ 2.1
x = ( -(-2) ± √4 +12 )/ 2
x = ( 2 ± √16 )/ 2
x = (2 + 4)/2
x1 = (2 – 4)/2 = -1
x2 = (2 + 4)/2 = 3
Sehingga dapat kita kita ketahui bahwa nilai x = -1 dan 3.
5. Berapakah perkiraan nilai x apabila persamaan kuadrat yang diketahui yaitu x2 + 8x + 12 = 0!
Jawab:
Diketahui persamaan kuadrat a = 1, b = 8, c = 12.
Sehingga dapat disubstitusikan ke dalam rumus persamaan kuadrat sebagai berikut:
x = ( -8 ± √b2 – 4ac )/ 2a
x = ( -8 ± √82 – 4.1.(12) )/ 2.1
x = ( -8 ± √64 – 48 )/ 2
x = ( -8 ± √16 )/ 2
x = (-8 + 4)/2
x1 = (-8 – 4)/2 = -6
x2 = (-8 + 4)/2 = -2
Sehingga dapat kita kita ketahui bahwa nilai x = -6 dan -2.
6. Dengan memakai rumus abc, tentukan himpunan penyelesaian dari x2 + 2x = 0!
Jawab:
Diketahui:
a = 1 , b = 1, c = 0
Sehingga akar – akar dari persamaan tersebut ialah sebagai berikut:
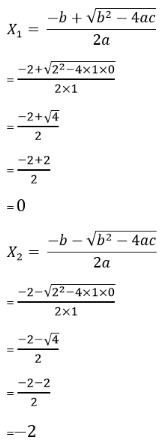
Sehingga dapat diketahui, hasil akar – akar dari persamaan x2 + 2x = 0 ialah x1= 0 dan x2= -2, sehingga himpunan penyelesaiannya adalah HP = { -2,0 }
7. Tentukan akar – akar dari persamaan 2x2 + 3x +5 = 0 dengan menggunakan rumus persamaan kuadrat.
Jawab:
Diketahui:
a = 2, b = 3, dan c = 5
Sehingga akar – akar dari persamaan tersebut ialah sebagai berikut:
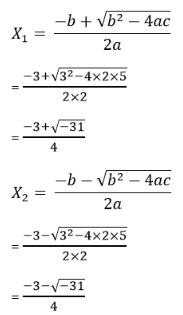
Hasil dari akar persamaan 2x2 + 3x +5 = 0 memiliki bilangan akar imajiner √–31, sehingga persamaan itu tidak memiliki penyelesaian.
Untuk himpunan penyelesaiannya ditulis sebagai himpunan kosong HP = { ∅ }.
8. Selesaikan akar – akar dari persamaan kuadrat x2 + 7x + 10 = 0 dengan memakai rumus persamaan kuadrat!
Jawab:
Diketahui:
a=1, b=7, dan c=10
Sehingga akar – akar dari persamaan tersebut ialah sebagai berikut:
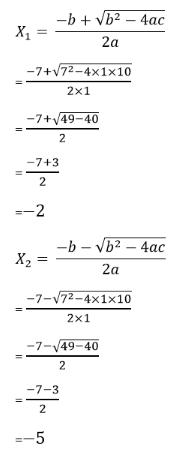
Sehingga dapat diketahui hasil akar – akar dari persamaan x2 + 7x + 10 = 0 ialah x = -2 atau x = -5.
9. Tentukan himpunan dari 3x2 – x – 2 = 0!
Jawab:
Diketahui:
a = 3, b = -1, c = -2
Sehingga akar – akar dari persamaan tersebut ialah sebagai berikut:
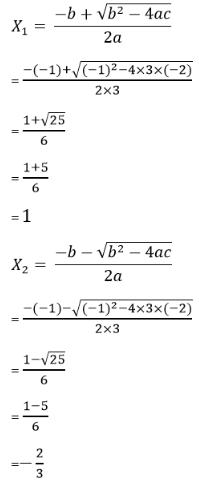
Sehingga akar – akar persamaan kuadrat 3x2 – x – 2 = 0 ialah x1=1 dan x2=-2/3.
Dan himpunan penyelesaiannya yaitu HP = { 1,-2/3 }.
10. Tentukan hasil persamaan kuadrat x2 + 12x + 32 = 0 dengan memakai rumus persamaan kuadrat!
Jawab:
Diketahui:
a = 1, b=12, dan c =32
Sehingga akar – akar dari persamaan tersebut ialah sebagai berikut:
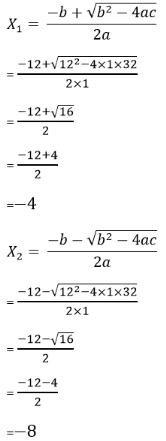
Sehingga hasil akar – akar persamaan kuadratnya yaitu -4 dan -8.