Materi Gerak Parabola: Rumus dan Contoh Soal

Rumus gerak Parabola biasanya menjadi salah satu rumus yang dicari. Pada dasarnya, gerak parabola juga dikenal sebagai gerak peluru. Diberi nama gerak parabola karena lintasan yang dimilikinya mempunyai bentuk parabola, bukan bergerak lurus.

Contoh dari gerak parabola juga dapat kita lihat dalam kehidupan sehari-hari, contohnya saja seperti gerakan benda yang dilempar dari pesawat hingga gerakan peluru Meriam yang sedang ditembakkan.

Pengertian Gerak Parabola

Gerak parabola merupakan gerakan dengan bentuk lintasan tidak lurus namun berbentuk parabola. Hal tersebut disebabkan karena adanya perpaduan GLB atau Gerak Lurus Beraturan dan GLBB atau Gerak Lurus Berubah Beraturan.

Kedua gerak ini akhirnya membentuk sebuah sudut elevasi di sumbu horizontal atau X serta sumbu vertikal atau Y. Sumbu X adalah GLB sedangkan sumbu Y adalah GLBB. Sehingga, keduanya memiliki lintasan melengkung dengan sebutan gerak parabola.

Gerak parabola awalnya didorong kecepatan awal dan kemudian menempuh lintasan dengan arah dipengaruhi gravitasi. Sebutan gerak peluru pada gerak parabola disebabkan karena jenis gerakan saat peluru ditembakkan juga mempunyai lintasan yang sama.

Ada berbagai karakteristik dari gerak parabola, yaitu:

1. Gerak parabola benda yang disebabkan karena gaya yang diberikan. Di dalam bahasan dinamika di ilmu fisika, gaya merupakan penyebab gerakan benda. Di bahasan gerak parabola, kita lebih fokus pada gerak benda sesudah dilempar serta bergerak bebas di udara.
2. Layaknya gerak jatuh bebas, benda yang melakukan gerak parabola ini dipengaruhi gaya gravitasi serta memiliki arah ke bawah atau pusat bumi sebesar g = 9.8 m/s2.
3. Adanya hambatan yang membuat benda saat ditembakkan, dilempar atau ditendang dengan kecepatan awal, gerakan bergantung dari gravitasi serta hambatan.

Baca: Rumus Daya

Ciri Ciri Gerak Parabola

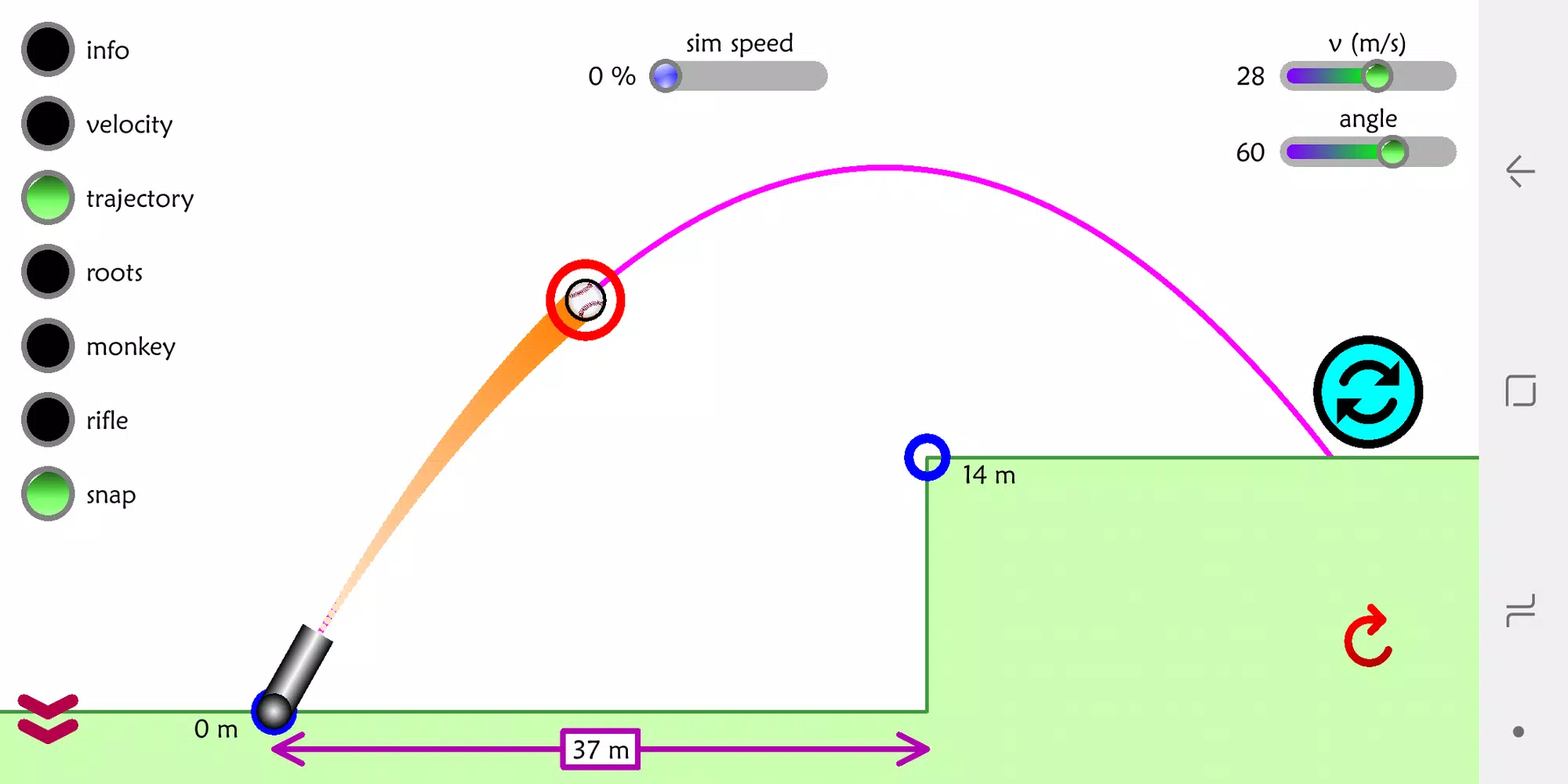
Berikut berbagai macam ciri yang dimiliki gerak parabola, yaitu:

1. Gerak terjauh ditempuh menggunakan sudut 45°
2. Pasangan sudut yang menghasilkan sudut dengan angka 90° nantinya dapat menghasilkan jarak tempuh yang sama
3. Massa tidak memiliki pengaruh pada sudut elevasi selama kecepatan di awal konstan

Baca: Rumus Transformator

Rumus Gerak Parabola

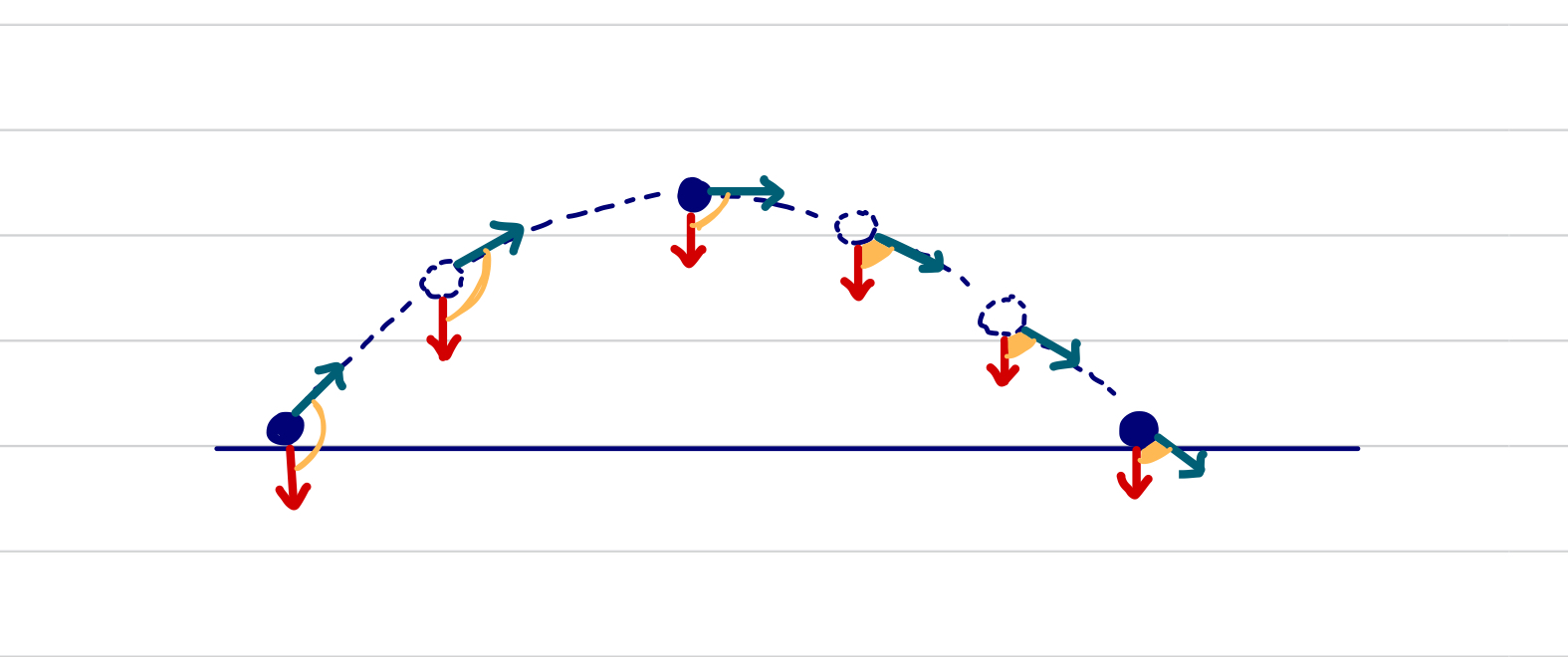
Bagaimana dengan rumus? Untuk rumus dari gerak parabola ini ada beberapa. Berikut beberapa diantaranya, seperti:

1. Rumus Gerak Parabola Pada Titik Awal

Pada dasarnya, peluru yang ditembak memiliki kecepatan awal. Ketika membentuk lintasan melengkung akan terdapat sudut dibentuk. Oleh sebab itu, nantinya kita akan memasukkan sudut di perhitungan kecepatan awal.

Dengan ini, kita memperoleh persamaan kecepatan awal untuk gerak horizontal (V_0x) serta vertikal (V_0y), yaitu:

• Kecepatan awal pada gerak horisontal (V_0x)

V_0x = V cos θ

• Kecepatan awal pada gerak vertikal (V_0y)

V_0y = V sin θ

• Kecepatan awal (V)

V = √V_0x+ V_0y

Keterangan:

• V = kecepatan awal
• V_0x= kecepatan awal sumbu x
• V_0y= kecepatan awal sumbu y
• θ = sudut yang dibuat terhadap sumbu x positif

2. Rumus Gerak Parabola Pada Titik A

Setelah memahami penjelasan rumu di atas, maka gerak pada sumbu X dianalisis dengan GLB. Oleh sebab itu, untuk kecepatan sama dengan kecepatan V_0x. Sedangkan V_y akan terdorong oleh gravitasi yang menarik serta unik benda ke bawah sehingga kecepatan akan berkurang.

Untuk jarak horizontal akan menggunakan rumus jarak GLB sedangkan jarak vertikal atau tinggi menggunakan rumus GLBB. Dengan persamaan ini, terdapat persamaan, yakni:

• Kecepatan sumbu x

V_x = V_0x = V cos θ

• Kecepatan sumbu y

V_y = V_0y – gt
V_y = V sin θ – gt

• Jarak di sumbu x

X = V_0x . t

• Jarak di sumbu y

Y = V_0y . t –

1 / 2

gt²

Keterangan

• V = kecepatan awal
• V_0x= kecepatan awal sumbu x
• V_x= kecepatan sumbu x
• V_0y= kecepatan awal sumbu y
• V_y= kecepatan di sumbu y
• g = gravitasi
• t = waktu tempuh
• θ = sudut yang dibuat terhadap sumbu x positif
• X = jarak terhadap sumbu x
• Y = jarak terhadap sumbu y

3. Rumus Gerak Parabola Pada Titik B

Titik B merupakan titik tertinggi yang disimbolkan sebagai h atau y_maks. Agar sebuah benda bisa mencapai ketinggian maksimal, syaratnya V_y = 0. Sehingga kecepatan di titik tertinggi yakni pada sumbu x (V_x ). Berikut merupakan persamaan yang bisa dirumuskan saat berada di titik B maksimal:

a. Titik tertinggi yang bisa dicapai
h =

V_0y² / 2g

h =

V² sin² θ / 2g

b. Waktu untuk mencapai titik tertinggi (B)
V_y = 0
V_y = V_0y – gt
0 = V sin θ – gt
t =

(V x sin θ) / g

t =

V_0y / g

c. Jarak horizontal dari titik awal sampai titik B
X = V_0x x t
X = V cos θ x

V sin θ / g

X =

V² x cos θ x sin θ / g

X =

V² x sin 2θ / g

Keterangan

• V : kecepatan awal
• V_0x:kecepatan awal di sumbu x
• V_x: kecepatan sumbu x
• V_0y: kecepatan awal di sumbu y
• V_y: kecepatan sumbu y
• g : gravitasi
• t : lama tempuh satuan waktu
• X : jarak terhadap sumbu x
• h : tinggi maksimum

4. Rumus Gerak Parabola Titik C

Pada gerak di titik C, sebenarnya sama serta menyerupai gerak parabola di titik A. Namun perbedaannya ada pada gerak gravitasi yang memiliki nilai factual. Hal tersebut disebabkan karena menuju ke bawah.

Karena dikatakan sama serta menyerupai melalui A, gerak di sumbu X akan tetap menggunakan GLB sedangkan Y akan menggunakan GLBB tetapi gravitasi yang dimilikinya mempunyai nilai positof. Dengan persamaan ini, terdapat beberapa persamaan, yakni:

• Kecepatan pada sumbu x

V_x = V_0x = V cos θ

• Kecepatan pada sumbu y

V_y = V_0y + gt
V_y = V sin θ + gt

5. Rumus Gerak Parabola Pada Titik D

Titik D merupakan jarak terjauh yang bisa dilalui benda yang melakukan gerak parabola. Jarak terjauh bisa disimbolkan dengan X_maks. Jarak maksimal ini juga bisa dikatakan sebagai jarak sebuah objek kembali ke tanah setelah objek melakukan gerakan parabola.

Waktu yang diperlukan sebuah benda untuk sampai ke tanah yakni 2 kali waktu benda untuk mencapai jarak saat ada di titik tertinggi. Berikut persamaannya:

Kecepatan pada sumbu x
V_x= V_0x = V . cos θ

Kecepatan pada sumbu y
V_y= V sin θ + gt

Waktu yang dibutuhkan hingga ke tanah (titik D)t = 2.

V_0y / g

t =

V . sin θ / g

Jarak maksimum (Jarak dari awal bola bergerak hingga titik D)

X_maks= V² sin 2θ / 2g

Keterangan

• V : kecepatan awal
• V_0x: kecepatan awal sumbu x
• V_x: kecepatan  sumbu x
• V_0y: kecepatan awal sumbu y
• V_y: kecepatan sumbu y
• g : gravitasi
• t : waktu tempuh
• X : jarak terhadap sumbu x
• X_maks: jarak maksimum

Baca: Rumus Massa Jenis

Komponen Gerak Parabola

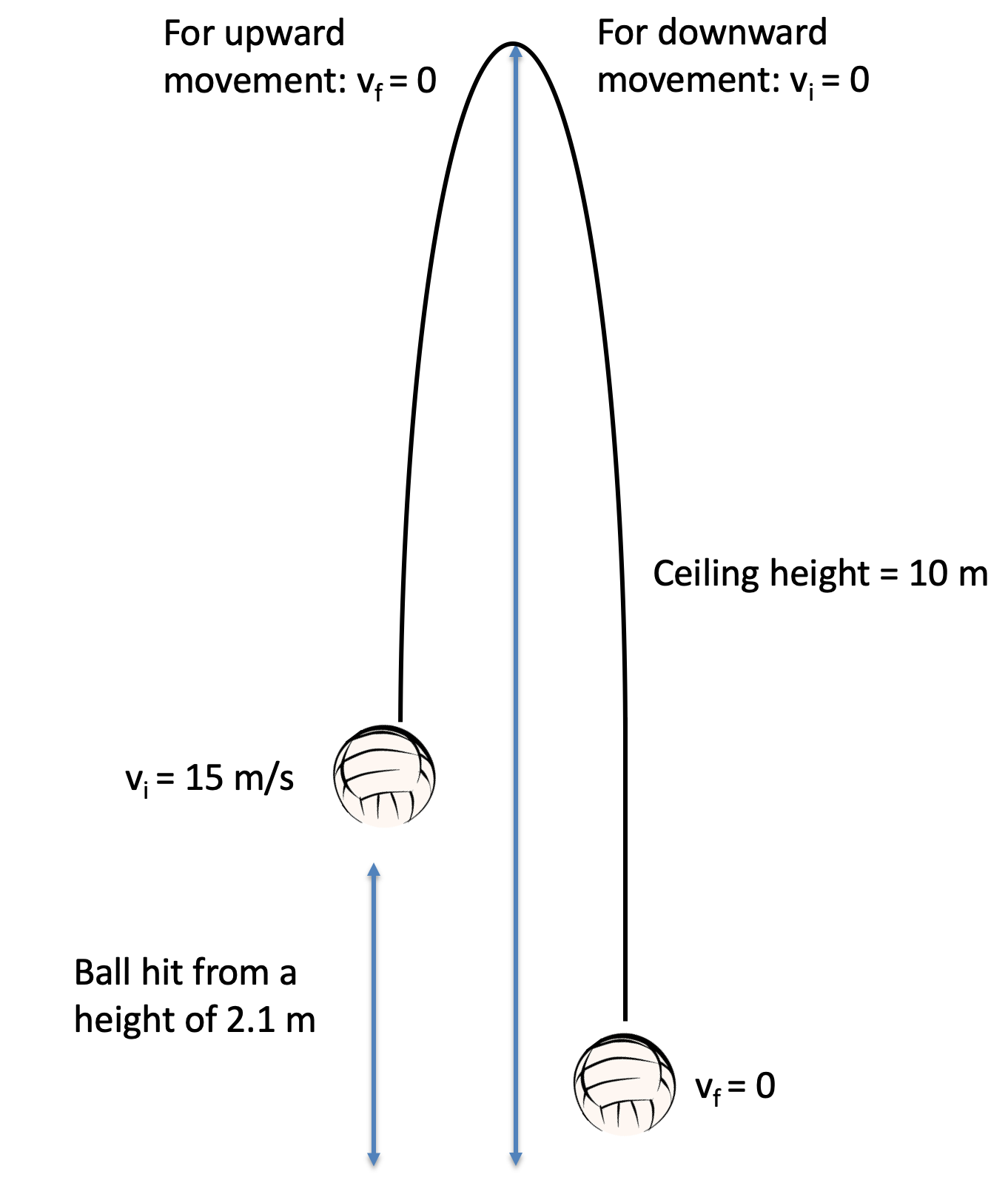
Seperti pada materi gerak parabola, gerak ini memiliki komponen, yaitu:

1. Komponen Gerak Sisi Horizontal

Komponen gerak horizontal memiliki besaran yang selalu tetap dalam setiap rentang waktu, hal ini disebabkan karena tidak ada percepatan serta perlambatan sumbu X.

Selain itu juga terdapat sudut antara kecepatan benda serta komponen gerak horizontal dalam setiap rentang waktu. Terakhir, tidak terdapat percepatan dan perlambatan di sumbu X.

2. Komponen Gerak Parabola Pada Sisi Vertikal

Sedangkan untuk gerak vertikal, memiliki besaran yang selalu berubah-ubah dalam setiap rentang, hal ini disebabkan karena pengaruh percepatan gravitasi di sumbu y.

Contoh Soal Gerak Parabola

Agar materi mengenai gerak parabola lebih jelas, berikut contoh soalnya:

Salah satu peluru jatuh tepat 10 meter di depan Sandra serta sudut elevansi yang dimilikinya 45 derajat. Tentukan kecepatan awal peluru tersebut

Jawab:

Andi menendang bola dengan kecepatan awal 15 m/s, serta memiliki sudut elevasi 45 derajat. Tentukan panjang lintasan maksimal bola

Jawab:

Rumus gerak parabola memang tidak semudah seperti yang dibayangkan untuk dihafalkan. Namun dengan latihan soal secara terus menerus, kita akan terbiasa untuk mengerjakannya.