Pada kesempatan kali ini, kita akan membahas terkait rumus gerak lurus berubah beraturan atau biasa disebut sebagai GLBB.
Namun sebelum itu, kalian juga harus mengetahui pengertian dari gerak lurus berubah beraturan itu sendiri dan juga contoh soalnya.
Selengkapnya simak ulasan di bawah ini baik baik ya.
Daftar Isi
Pengertian GLBB

GLBB merupakan suatu gerak lurus berubah beraturan, yang mana artinya ialah suatu benda bergerak pada lintasan lurus dengan kecepatan tak konstan serta percepatannya konstan.
Dari pengertian tersebut, maka bisa kita tulis menjadi:
v ≠ konstan
a = konstan
Ciri – Ciri Gerak Lurus Beraturan
Sebuah benda dapat disebut bergerak lurus berubah beraturan (GLBB) apabila mempunyai ciri utama sebagai berikut:
- Memiliki lintasan yang garis lurus.
- Kecepatan benda dapat berubah – ubah secara teratur.
- Percepatan benda tetap atau konstan.
Ciri utama pada gerak lurus berubah beraturan bahwasanya dari waktu ke waktu kecepatan benda akan mulai berubah, semakin lama akan semakin cepat atau lambat sehingga gerakan pada benda itu dari waktu menuju waktu akan mengalami percepatan atau perlambatan.
Cara untuk membedakan sebuah benda termasuk dalam GLB atau GLBB sebetulnya sangat mudah.
Pada benda yang mengerjakan gerak lurus beraturan atau GLB, maka kecepatan benda akan selalu tetap atau konstan sehingga tidak terdapat istilahnya kecepatan awal, kecepatan akhir, diam, berhenti, percepatan maupun gravitasi bumi.
Tetapi jika benda yang mengerjakan GLBB maka akan terdapat istilah kecepatan awal, kecepatan akhir, diam, berhenti, percepatan maupun gravitasi bumi.
Jenis – Jenis GLBB
Pada GLBB di bagi ke dalam dua jenis yang berbeda, yakni GLBB dipercepat dan diperlambat. Berikut penjelasannya:
1. GLBB Dipercepat
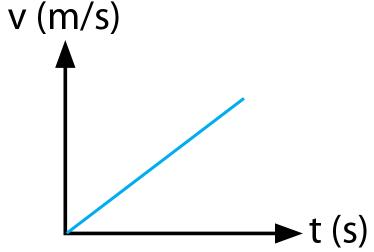
Gambar grafik yang ada di bawah ini adalah grafik kecepatan pada waktu GLBB dipercepat.
2. GLBB Diperlambat
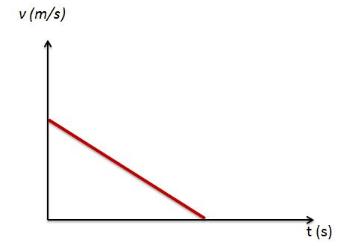
Gambar grafik yang ada di bawah ini adalah grafik kecepatan pada waktu GLBB diperlambat.
Rumus GLBB
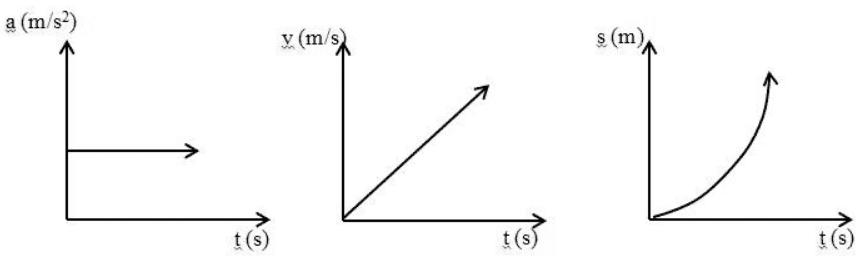
Persamaan atau rumus pada GLBB memakai suatu tanda positif (+) dan juga negatif (-) yang tergantung dengan dipercepat atau diperlambatnya suatu gerak.
Berikut ini adalah rumus atau persamaan dari GLBB yang perlu kalian ketahui:
vt2 = v02 + 2.a.s
vt = v0 + a.t
s = v0.t + 1/2.a.t2
Keterangan:
- v0: Kecepatan awal (m/s)
- v: Kecepatan (m/s)
- a: Percepatan (m/s2)
- t: Waktu (s)
- s: Jarak (m)
Contoh GLBB
Berikut ini adalah beberapa benda yang dapat dikatakan mengerjakan suatu Gerak lurus berubah beraturan (GLBB), antara lain:
- Benda tersebutjatuh bebas. Benda jatuh bebas dari arah ketinggian tertentu, maka semakin lama kecepatannya akan menjadi semakin besar. Seperti buah jatuh dari pohon
- Naik sepeda tanpa me-kayuh di jalanan yang dikategorikan menurun. Maka sepeda tersebut akan bergerak semakin lama semakin cepat.
- Naik mobil di jalan yang lurus dengan menginjak pedal gas teratur. Gerak mobil nantinya semakin lama akan semakin cepat/ kebut.
Di dalam kehidupan sehari – hari, kebanyakan gerak di dalam sebuah benda kecepatannya berubah pada setiap waktu. Dapat dipercepat atau diperlambat.
Seperti contoh di atas yang kebanyakan adalah benda yang jatuh dari arah ketinggian tertentu, dimana kecepatannya sedikit demi sedikit akan berubah.
Percepatan yang semakin cepat atau semakin lambat itulah yang disebut sebagai gerak lurus berubah beraturan.
Contoh Soal
Setelah membaca uraian yang ada di atas, untuk memudahkan kalian dalam memahaminya, berikut ini akan kami berikan beberapa contoh soal beserta pembahasan nya, simak baik – baik ya!
1. Contoh Pertama
Pada mulanya, Pak Turitno mengendarai sebuah motor dengan menggunakan kecepatan tetap 40 m/s. Namun tiba – tiba, motor itu di rem sehingga mengalami perlambatan sebesar 20 m/s2.
Hitunglah jarak yang ditempuh oleh motor itu hingga hingga berhenti!
Jawab:
Diketahui:
- v0 = 40 m/s
- vt = 0 m/s
- a = -20m/s2
Ditanya:
s?
Pembahasan:
vt = v0 + a.t
0 = 40 – 20.t
t = 2 s
Jarak yang ditempuh selama waktu 2 s:
s = v0.t + 1/2.a.t2
s = 40.2 + 1/2.(-20).22
s = 80 + (-40)
s = 40 m
Sehingga dapat diketahui bahwa jarak yang ditempuh oleh motor itu agar bisa berhenti ialah 40 m.
2. Contoh Kedua
Suatu bola mula – mula dalam kondisi diam di lantai yang licin, lalu bola tersebut didorong sampai mengalami percepatan sebesar 4 m/s2.
Hitunglah kecepatan bola selepas bergerak selama waktu 8 sekon!
Jawab:
Diketahui:
- v0 = 0 m/s
- a = 4 m/s2
- t = 8 s
Ditanya:
v8?
Pembahasan:
v8 = v0 + a.t
v8 = 0 + 4.8
v8 = 32 m/s
Sehingga dapat kita ketahui bahwa kecepatan bola selepas bergerak 8 sekon ialah 32 m/s.
3. Contoh Ketiga
Di dalam sebuah perlombaan kuda, seekor kuda dapat berlari dengan kecepatan awal 4 m/s serta percepatan 4 m/s2.
Maka hitunglah kecepatan kuda selepas menempuh jarak 30 meter!
Jawab:
Diketahui:
- v0 = 4 m/s
- a = 4 m/s2
- s = 30 m
Ditanya:
vt?
Pembahasan:
vt2 = v02 + 2.a.s
vt2 = 16 + 2.4.30
vt2 = 256
vt = 16 m/s
Sehingga dapat kita ketahui bahwa kecepatan kuda selepas menempuh jarak 30 meter ialah 16 m/s.
4. Contoh Keempat
Suatu motor balap di rem dengan perlambatan konstan dari kelajuan 50 m/s ke 30 m/s pada jarak 80 m.
Jarak total (dalam meter) yang sudah ditempuh oleh motor itu hingga akhirnya dapat berhenti ialah?
Jawab:
Diketahui:
- v1 = 50 m/s
- v2 = 30 m/s
- s12 = 80 m
Pembahasan:
v22 = v12 + 2.a.s12
900 = 2500 + 2.a.80
a = -10 m/s2 …(1)
v32 = v12 + 2.a.s13
0 = 2500 + 2.(-10).s13
s13 = 125 m …(2)
Sehingga dapat kita ketahui bahwa jarak yang ditempuh oleh motor balap hingga sampai berhenti ialah 125 m.
5. Contoh Kelima
Benda yang pada mulanya berkecepatan 20 m/s berubah menjadi 5 m/s selepas menempuh jarak 8 meter.
Berapa jauh lagi jarak yang dapat ia tempuh sampai berhenti?
Jawab:
Langkah pertama tentukan nilai perlambatan (-a):
Vt² = V0² + 2 × a × s
5² = 20² + 2 × a × 8
25 – 400 = 16 × a
16 × a = -375
a = -23,4375 m/s²
Kemudian menentukan jarak selepas 8 meter:
Vt² = V0² + 2 × a × s
0² = 5² + 2 × (-23,4375) × s
46,875 × s = 25
s = 1,875 meter
Sehingga dapat kita ketahui bahwa total jarak yang ditempuh benda tersebut ialah:
s = 8 + 1,875 = 9,875 meter.