Kamu tentu sudah familiar dengan bentuk dari bangun ruang kerucut, bukan? Memiliki bentuk unik seperti nasi tumpeng, kerucut mempunyai tampilan unik yang menjadi ciri khasnya. Namun, tahukah kamu bagaimana cara menghitung volume dan luas kerucut menggunakan rumus kerucut?
Bagi kamu yang berstatus sebagai pelajar atau mahasiswa jurusan Matematika, pasti akan menghadapi soal mengenai cara menghitung luas dan volume bangun ruang kerucut. Oleh sebab itulah, kamu harus mempelajari dan memahami cara menggunakan rumus dari kerucut.
Daftar Isi
Pengertian Kerucut

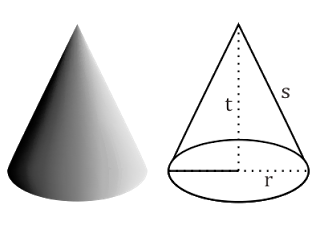
Kerucut adalah jenis bangun ruang yang mempunyai alas berbentuk lingkaran dengan selimut beriris. Sisi tegak kerucut berupa suatu bidang miring yang juga dikenal sebagai selimut kerucut. Sementara itu, sisi lain pada bangu ruang ini disebut dengan alas kerucut.
Secara umum, kerucut hanya mempunyai dua sisi dengan satu rusuk. Kerucut juga akrab disebut limas segi-n tak terhingga atau sisi alas lingkaran. Sebagaimana bola dan tabung, kerucut dikategorikan sebagai bangun ruang sisi lengkung karena mempunyai sisi berbentuk lengkungan.
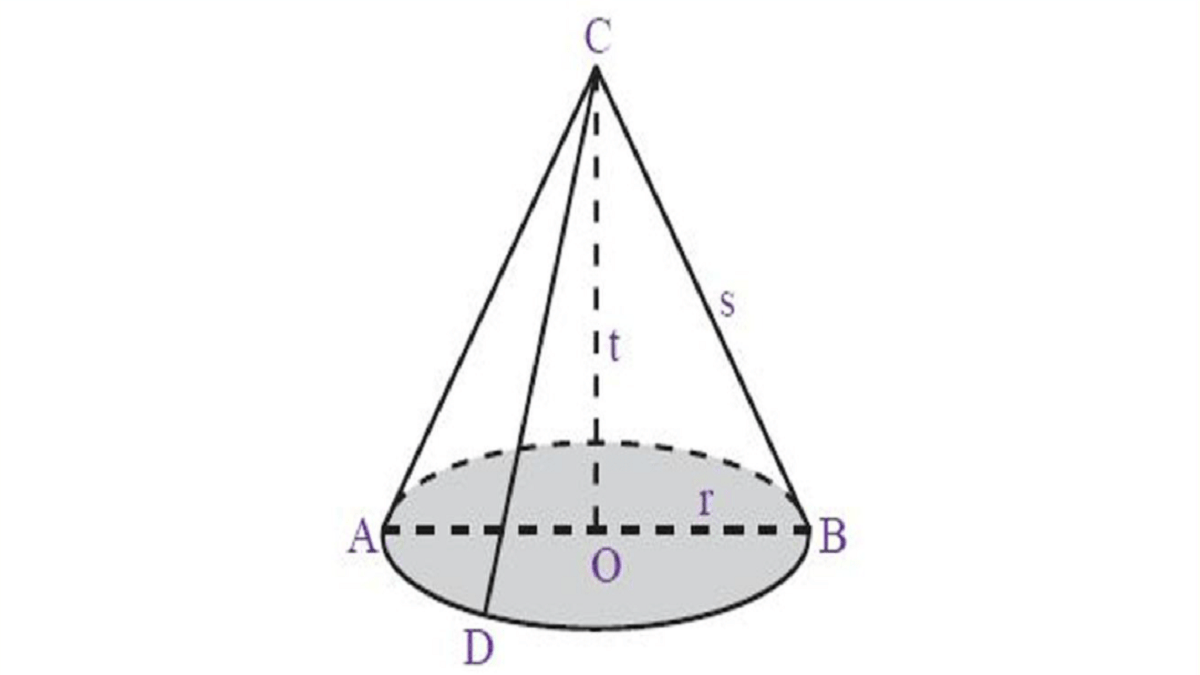
Kerucut terdiri atas beberapa unsur atau elemen penting, diantaranya adalah sebagai berikut:
- Bidang alas : Daerah yang diarsir atau sisi berbentuk lingkaran.
- Diameter alas : Ruas dari garis di kedua sisi.
- Jari-jari alas : Garis bagian tengah yang memanjang dari atas ke bawah.
- Selimut kerucut : Sisi kerucut yang tidak diarsir.
- Tinggi kerucut : Jarak dari titik puncak hingga pusat bidang alas.
- Garis pelukis : Garis-garis pada selimut kerucut dari titik puncak ke lingkaran alas.
Sementara itu, kerucut juga memiliki beberapa sifat seperti di bawah ini:
- Memiliki dua sisi, alas lingkaran dan sisi lengkung.
- Mempunyai satu rusuk melengkung.
- Terdapat satu titik puncak.
- Tidak mempunyai rumus titik sudut.
Baca: Bangun Datar
Ciri Ciri Kerucut
Apabila kamu memperhatikan gambar kerucut secara detail, maka akan melihat adanya karakteristik yang menjadi ciri khasnya. Untuk lebih jelasnya, di bawah ini adalah ciri-ciri bangun ruang kerucut:
- Memiliki 1 rusuk
- Terdiri dari 2 sisi
- Memiliki 1 titik puncak
- Jaring-jaring dengan bentuk lingkaran serta juring lingkaran
- Memiliki luas permukaan
- Mempunyai volume
- Kerucut adalah bangun ruang berbentuk limas dengan alas lingkaran
Baca: Irisan Kerucut
Rumus Luas Permukaan Kerucut
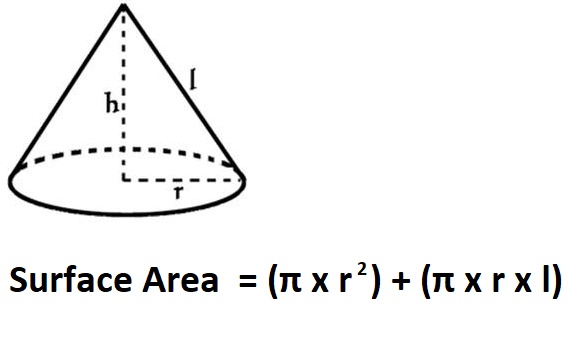
Setelah memahami pengertian dan ciri-ciri kerucut. Kamu juga harus tahu cara menghitung bangun ruang ini dengan menggunakan rumus-rumus jitu. Untuk mencari luas permukaan kerucut atau luas alas dan luas selimutnya, maka kamu dapat menerapkan rumus menghitung luas kerucut.
Dalam kasus ini, maka perlu terlebih dahulu membuat jaring-jaring kerucut yang terdiri dari lingkaran serta juring lingkaran. Sementara itu, rumus yang digunakan adalah sebagai berikut:
Keterangan:
Luas lingkaran = π x r2
Luas juring lingkaran = π x r x s
Luas permukaan kerucut = Luas lingkaran + luas juring lingkaran
Pembahasan:
π = 3,14 atau 22/7
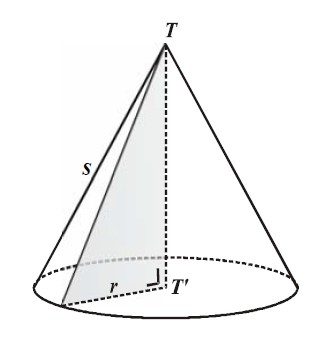
r = Jari-jari kerucut
s = Garis pelukis kerucut (garis dari puncak sampai rusuk kerucut)
Baca: Bangun Ruang Sisi Lengkung
Contoh Soal Luas Permukaan Kerucut
Setelah mengetahui rumus kerucut, tepatnya untuk mencari luas permukaan kerucut. Kamu mungkin masih merasa bingung bagaimana cara menerapkannya agar dapat menyelesaikan soal.
Di bawah ini adalah beberapa contoh soal mengenai menghitung luas permukaan kerucut:
1. Soal 1
Suatu bangun ruang kerucut mempunyai panjang jari-jari alas 5 cm dan tinggi 10 cm. Lantas, berapakah luas kerucut tersebut? (π = 3,14)
Pembahasan:
r = 5 cm
t = 10 cm
S2 = r2 + t2
S2 = 52 + 102 = 25 + 100 = 125
S = √ 125 = 12.5
Luas sisi kerucut = πr (r + s)
= 3,14 x 5 x 5 x (5 + 12.5) = 3,14 x 5 x 17.5 = 274,75
Jadi, dapat diketahui bahwa luas sisi kerucut adalah 274,75.
2. Soal 2
Terdapat bangun ruang kerucut berjari-jari 15 cm dan panjang pelukis 25 cm. Sekarang, cari dan hitunglah luas dari kerucut tersebut!
Diketahui:
r = 15 cm
s = 25 cm
Pertanyaan: Luas kerucut?
Penyelesaian:
L = πr (r + s)
L = 3,14 x 15 (15 + 25)
L = 3,14 x 15 x 40
L = 1.884 cm2
Jadi, diketahui bahwa luas kerucut adalah 1.884 cm2.
3. Soal 3
Ada kerucut yang mempunyai jari-jari 16 cm dan panjang garis pelukis 31 cm. Sekarang, cari dan hitung luas kerucut tersebut!
Diketahui:
r = 16 cm
s = 31 cm
Pertanyaan: Luas kerucut?
Jawaban:
L = πr (r + s)
L = 22/7 x 16 (16 + 31)
L = 22/7 x 16 x 47
L = 2.363 cm2
Dapat disimpulkan, bahwa luas kerucut adalah 2.363 cm2
4. Soal 4
Sebuah kerucut memiliki jari-jari 19 cm dengan panjang garis pelukis 29 cm. Sekarang, coba cari dan hitunglah luas dari kerucut tersebut!
Diketahui:
r = 19 cm
s = 29 cm
Pertanyaan : Luas?
Jawaban:
L = πr (+s)
L = 22/7 x 19 (19 + 29)
L = 22/7 x 19 x 48
L = 2,866 cm2
Jadi, luas dari bangun datar kerucut tersebut adalah 2,866 cm2.
Baca: Rumus Segitiga
Rumus Volume Kerucut
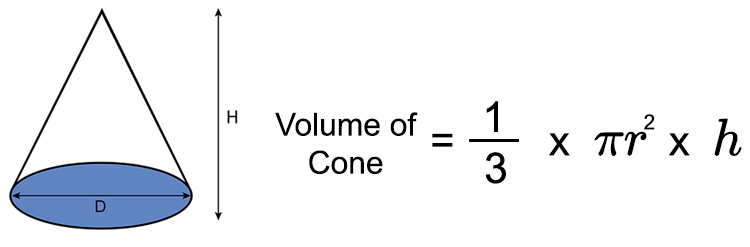
Perlu diketahui, bahwa rumus kerucut untuk menghitung volume, sebenarnya merupakan kombinasi dari rumus luas lingkaran dan volume limas. Pasalnya, seperti diketahui jika kerucut adalah suatu bangun ruang limas yang mempunyai alas dengan bentuk lingkaran.
Rumus volume limas:
Dari rumus tersebut, dapat diketahui bahwa rumus menghitung volume kerucut adalah:
Keterangan:
π = 22/7 (3,14)
r = Jari-jari kerucut
t = Tinggi kerucut
Contoh Soal Volume Kerucut
Supaya lebih mudah dalam mencari volume bangun ruang kerucut. Kamu bisa menjadikan dua contoh soal yang ada di bawah ini sebagai panduan belajar:
1. Soal 1

Jika topi ulang tahun berbentuk kerucut yang memiliki ukuran jari-jari 30 cm dengan tinggi 15 cm, lalu berapa volume dari topi tersebut?
Pembahasan:
r = 30 cm
t = 15 cm
v = x luas alas x tinggi
v = x πr2 x t
v = πr2 t
v = x x 302 cm x 15 cm
v = 4.530 cm3
Dapat disimpulkan bahwa volume topi tersebut adalah 4.530 cm3.
2. Soal 2

Jika sebuah lingkaran mempunyai luas 30 cm2. Apabila lingkaran tersebut dibuat kerucut dengan ketinggian 10 cm, maka hitunglah volume kerucut tersebut.
Pembahasan:
t = 10 cm
Luas : L = π x r2 = 30 cm2
v = 1/3 x π x r2 x t
= 1/3 x 30 x 10 (π x r2 = 30 cm2)
= 100 cm3
Dengan begitu, dapat disimpulkan bahwa volume kerucut adalah 100 cm3.
Rumus kerucut digunakan untuk memecahkan soal yang berhubungan dengan bangun ruang kerucut, baik volume, luas, maupun alas. Dengan memahami rumusnya, maka tidak akan sulit untuk memecahkan berbagai macam soal yang berkaitan dengan kerucut.