Segitiga merupakan suatu bangun datar yang dibentuk oleh tiga garis lurus yang saling berpotongan. Berikut ini akan kami berikan informasi selengkapnya mengenai rumus segitiga.
Segitiga dibentuk oleh 3 buah titik sudut yang posisinya tidak segaris dihubungkan.
Pada setiap segitiga selalu berlaku beberapa sifat, diantaranya yaitu;
- jumlah panjang dua sisi selalu lebih besar dibandingkan dengan panjang sisi segitiga;
- jumlah sudut-sudut suatu segitiga adalah 180 derajat;
- sudut terbesar merupakan sudut yang menghadap sisi terpanjang, sementara sudut terkecil merupakan sudut yang menghadap sisi terpendek;
- besar sudut luar sama dengan jumlah dua sudut yang tidak berpenglurus dengan sudut luar tersebut.
Mengenai segitiga, akan kita bahas selengkapnya di bawah ini.
Daftar Isi
Jenis Jenis Segitiga
Jenis atau macam segitiga dibagi menjadi dua macam, yakni ditentukan oleh panjang sisi-sisi dan besar sudut yang dimilikinya. Berikut penjelasannya masing-masig
Jenis segitiga berdasarkan dari panjang sisi-sisi, antara lain:
- Segitiga Sama Kaki: apabila ketiga sisi segitiga sama panjang.
- Segitiga Sama Sisi: apabila dua di antara sisi segitiga itu sama panjang.
- Segitiga Sembarang: apabila ketiga sisi segitiga tidak sama.
Jenis segitiga berdasarkan besar sudut, antara lain:
- Segitiga Lancip: apabila besar setiap sudut segitiga kurang dari 90 derajat (adalah sudut lancip).
- Segitiga Siku-siku: apabila salah satu sudut serta segitiga besarnya sama dengan 90 derajat.
- Segitiga Tumpul: apabbila salah satu sudut segitiga besarnya lebih besar dari 90 derajat.
Rumus Segitiga
1. Rumus Keliling Segitiga Siku-Siku
Segitiga siku-siku adalah segitiga dengan satu sisi miring, di mana jumlah salah satu sudutnya adalah 90 derajat.
Panjang sisi miring dapat kita ketahui apabila alas dan tingginya dikeahui, yakni dengan memakai dalil Pythagoras.
Adapun sifat dari segitiga siku-siku, diantaranya yaitu:
- Pertama, Segitiga siku siku mempunyai 2 sisi yang saling tegak lurus.
- Kedua, Segitiga siku siku memiliki 1 sisi miring serta salah satu sudutnya merupakan sudut siku siku.
- Ketiga, Segitiga siku siku tidak mempunyai simetri lipat dan simetri putar.
Perhatikan bangun segitiga berikut!
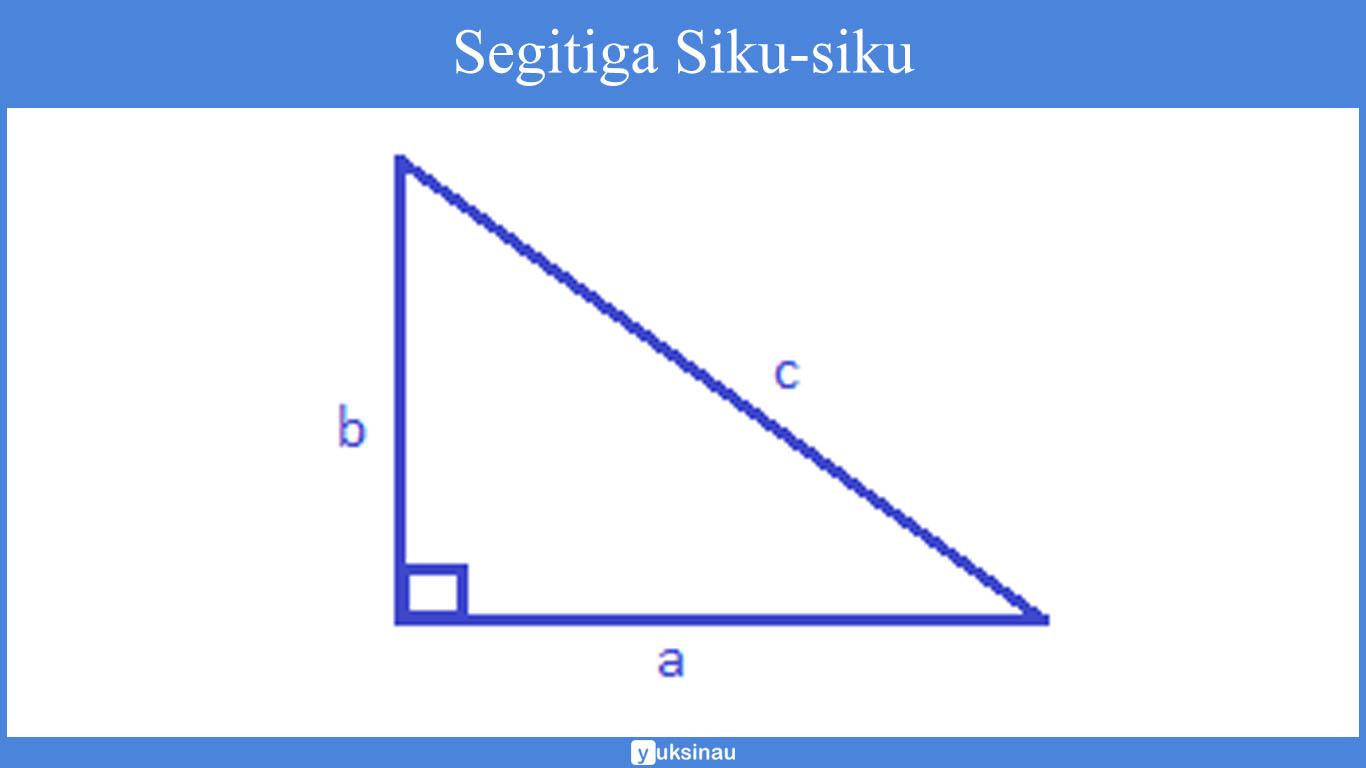
Keliling segitiga siku-siku di atas yaitu a + b + c.
Keterangan:
a = alas
b = tinggi
c = sisi miring (hipotenusa)
Panjang sisi c dapat kita ketahui asalkan panjang a dan juga b diketahui.
c = √(a² + b²)
Untuk mempermudah penulisan serta supaya tidak membingungkan, rumus di atas juga dapat kita ubah menjadi seperti berikut ini:
c² = a² + b²
Sebagai contoh:
a = 8 cm
b = 6 cm
c² = 8² + 6²
c² = 64 + 36 = 100
c = √100 = 10 cm
2. Rumus Keliling Segitiga Sama Sisi
Sesuai dengan namanya, jenis segitiga ini mempunyai sisi-sisi yang sama panjangnya.
Kita dapat menghitung keliling segitiga ini, meski hanya satu saja panjang sisi yang diketahui, sebab panjang salah satu sisinya sama dengan panjang sisi-sisi yang lain.
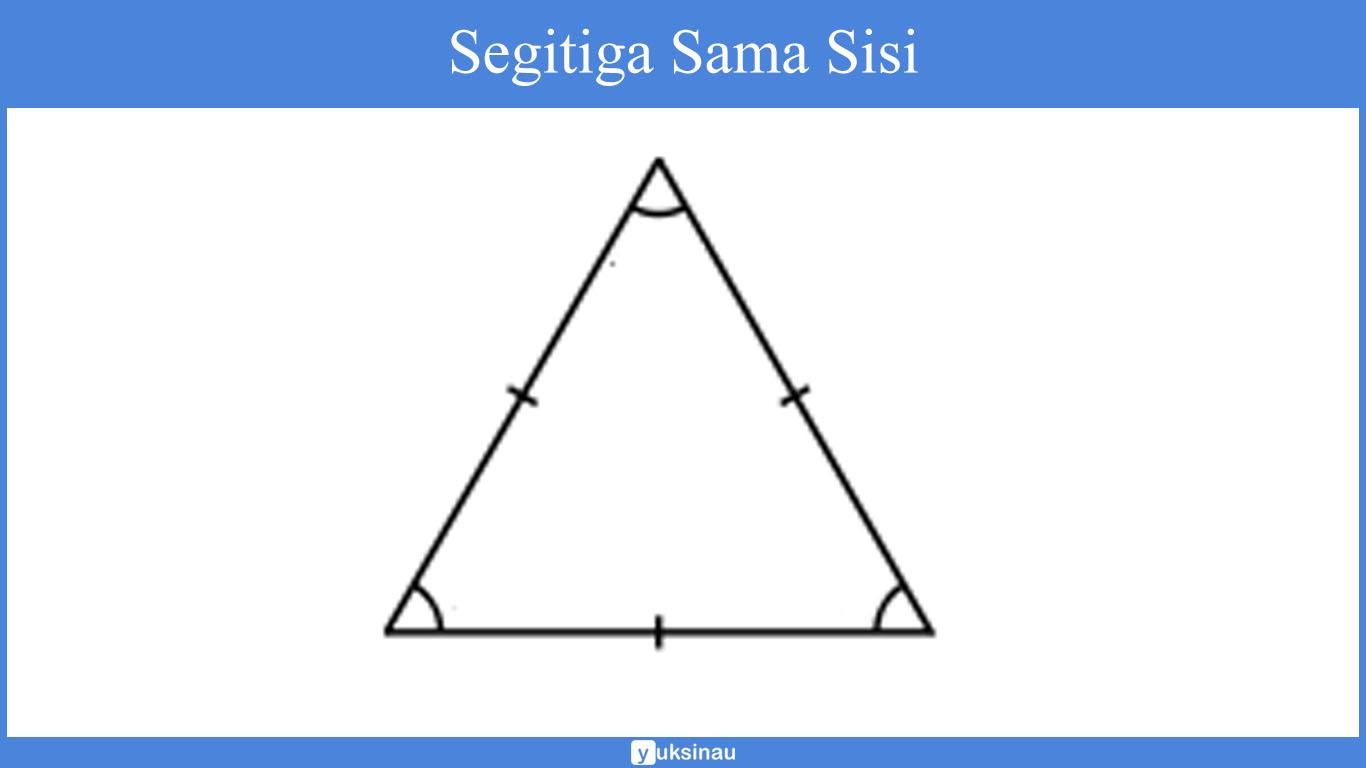
Keliling = a + b + c
Sebab a, b, dan c sama panjang, maka rumusnya dapat kita ubah menjadi seperti berikut ini:
Keliling = 3 x a atau 3 x b atau 3 x c
atau
Keliling = 3 x sisi
Sebagai contoh:
Hitunglah keliling segitiga sama sisi yang panjang salah satu sisinya 7 cm!
Keliling = 3 x 7 = 21 cm
3. Rumus Keliling Segitiga Sama Kaki
Segitiga sama kaki adalah segitiga yang mempunyai sepasang sisi miring sama panjang serta satu sisi sebagai alas.
Apabila ada salah satu sisi miring pada segitiga sama kaki, maka panjang sisi miring lainnya dapat kita ketahui , sebab kedua sisi miring pada segitga sama kaki sama panjang.
Untuk mencari keliling dari segitiga sama kaki, caranya yaitu dengan cara menjumlahkan alas dengan kedua sisi miring yang sama panjang.
Berikut ini adalah gambar dari segitiga sama kaki. Untuk alas kami tandai dengan huruf a, untuk sisi miring kami tandai dengan huruf b.
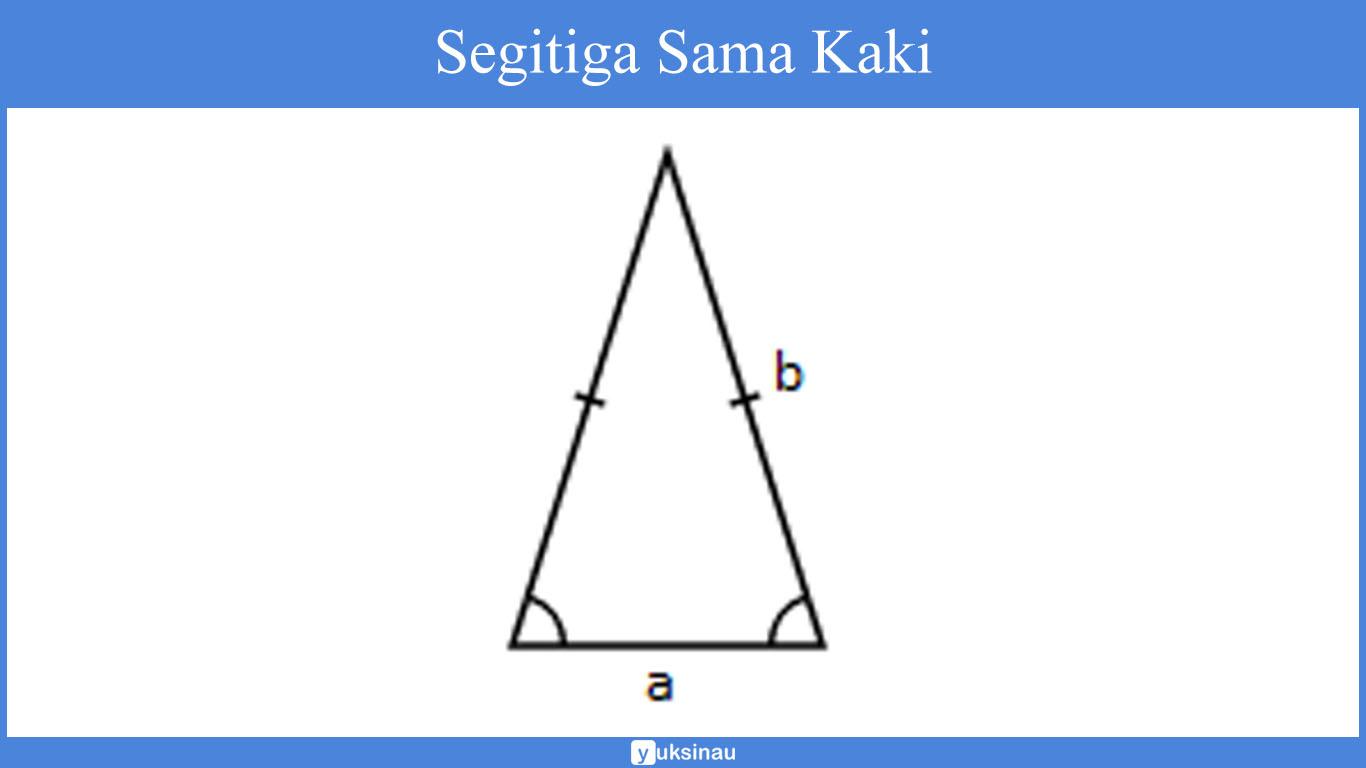
Keliling = 2 x a + b
Sehingga dari penjelasan di atas, dapat kita simpulkan bahwa rumus dari keliling segitiga yaitu:
Keliling (K) = sisi 1 + sisi 2 + sisi 3
Ingat, yang penting diingat yaitu konsep dari keliling itu sendiri. Rumus untuk menyederhanakan penulisan.
Apabila panjang sisi miringnya tidak diketahui, sementara tingginya diketahui, maka kita dapat hitung sisi miringnya dengan memakai rumus Pythagoras yang sudah kita bahas di atas.
4. Rumus Luas Segitiga
Rumus Luas Segitiga adalah salah satu rumus segitiga yang sangat mudah untuk dipahami sebab Rumus matematika segitiga hanya memakai panjang alas segitiga (a) dikali ½ dan dikali dg t / Tinggi Segitiga.
Luas = ½ .a.t
Rangkuman Materi Segitiga
Berikut akan kami berikan rangkuman dari rumus segitiga, antara lain:
| Nama | Rumus |
|---|---|
| Luas (L) | L = ½ × a × t |
| Keliling (Kll) | Kll = a + b + c |
| Tinggi (t) | t = (2 × Luas) ÷ a |
| Alas (a) | a = (2 × Luas) ÷ t |
Contoh Soal dan Pembahasan
Soal 1.
Suatu gambar segitiga memiliki panjang alas 20 cm dan tinggi sebesar 10 cm, maka hitunglah Luas Segitiga dan juga Keliling Segitiga tersebut.
Jawab:
- Mencari Luas Segitiga
Luas = ½.a.t
L = ½.20.10
L = ½ x 200 = 100 cm²
- Mencari Keliling Segitiga
Keliling = s + s + s
K = 20 + 20 + 20
K = 60 cm
Soal 2.
Terdapat Sebuah segitiga siku siku yang dengan panjang alasnya = 12 cm serta mempunyai tinggi = 10 cm. Cari dan hitunglah luas segitiga siku siku tersebut!
Jawab:
Diketahui:
a = 12 cm
t = 10 cm
Ditanya: luas =…?
Penyelesaian:
L = ½ x a x t
L = ½ x 12 x 10
L= 60 cm2
Sehingga, luas segitiga siku siku tersebut yaitu = 60 cm2
Soal 3.
Diketahui sebuah segitiga dengan panjang sisi alas a = 4 cm, sisi b = 3 cm, sisi c = 5 cm serta t = 3 cm.
Hitunglah keliling dan juga luas segitiga tersebut!
Jawab:
Diketahui:
a = 4 cm
b = 3 cm
c = 5 cm
t = 3 cm
Ditanya:
Keliling dan juga luas!
Penyelesaian:
Keliling = a + b + c
Keliling = 4 cm + 3 cm + 5 cm
Keliling = 12 cm
Luas = ½ × a × t
Luas = ½ × 4 cm × 3 cm
Luas = 6 cm²
Sehingga, keliling segitiga yaitu 12 cm serta luas segitiga 6 cm².
Soal 4. Mencai Tinggi Segitiga
Diketahui sebuah segitiga memiliki luas 18 cm² serta sisi alas 4 cm. Tentukan tinggi segitiga!
Diketahui:
Luas = 18 cm², a = 4 cm
Ditanya:
Tinggi segitiga!
Jawab:
Tinggi = (2 × Luas) ÷ a
Tinggi = (2 x 18 cm²) ÷ 4 cm
Tinggi = 36 cm² ÷ 4 cm = 9 cm
Sehingga, tinggi segitiga yaitu 9 cm.
Soal 5. Mencari Alas Segitiga
Diketahui sebuah segitiga memiliki luas 16 cm² dan tinggi 8 cm. Tentukan alas segitiga!
Diketahui:
Luas = 16 cm², a = 8 cm
Ditanya:
Alas segitiga!
Jawab:
Alas = (2 × Luas) ÷ t
Alas = (2 x 16 cm²) ÷ 8 cm
Alas = 32 cm² ÷ 8 cm = 4 cm
Sehingga, alas segitiga yaitu 4 cm.
Demikianlah ulasan singkat kali ini mengenai rumus segitiga yang dapat kami sampaikan. Semoga ulasan di atas mengenai Garis dan Sudut dapat kalian jadikan sebagai bahan belajar kalian.
Satu pemikiran pada “Rumus Segitiga”