Sebelum kalian mengetahui apa saja rumus yang ada pada bangun tabung, maka kalian harus mengetahui apa pengertian dari tabung itu sendir, selengkapnya simak ulasan di bawah ini.
Daftar Isi
Pengertian Tabung
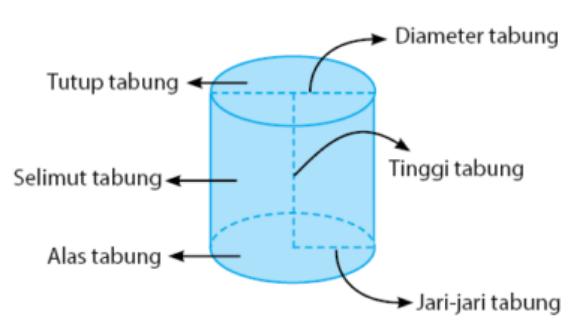
Tabung merupakan suatu bangun ruang yang disusun oleh 3 buah sisi yakni 2 buah lingkaran yang memiliki ukuran sama serta 1 segiempat yang menyelimuti atau mengelilingi kedua lingkaran itu.
Bangun tabung juga kerap disebut sebagai silinder (di dalam bahasa inggris “cylinder“).
Beberapa benda yang berbentuk tabung adalah kayu yang terpotong, pipa, drum, botol, bambu serta benda dengan bentuk yang sama lainnya.
Ciri – Ciri Tabung
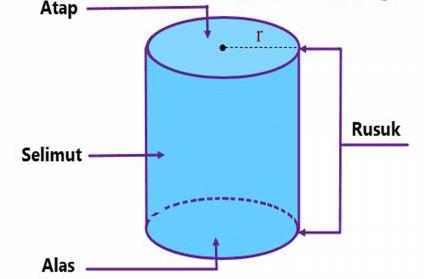
Bentuk tabung mempunyai beberapa ciri yang membedakannya dengan bentuk bangun lainnya, diantaranya yaitu:
- Mempunyai 2 buah rusuk.
- Mempunyai alas serta tutup yang bentuknya lingkaran.
- Mempunyai 3 bidang sisi berupa alas, tutup dan juga selimut.
Unsur – Unsur Tabung
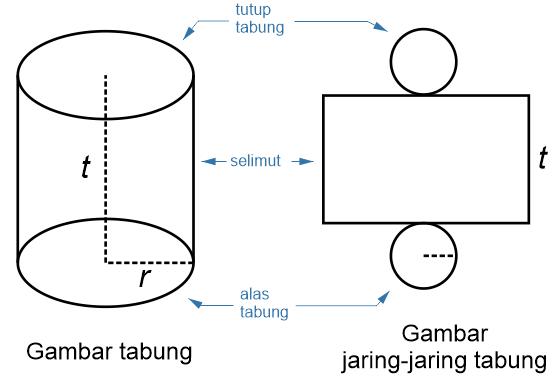
Adapun berbagai unsur pembangun tabung, diantaranya yaitu:
1. Sisi tabung
Sisi tabung merupakan bidang yang membentuk suatu tabung. Sisi tabung terdiri atas dua buah lingkaran serta satu buah selimut.
2. Selimut Tabung
Selimut tabung merupakan suatu bidang yang menutupi bentuk tabung. Selimut tabung mempunyai bentuk persegi panjang.
3. Diameter
Jika salah satu alas maupun tutup yang berbentuk lingkaran dipotong di tengah – tengah maka akan menjadi ukuran yang sama, dimana jarak potongan itu disebut sebagai diameter tabung.
4. Jari – jari
Jari – jari merupakan setengah dari diameter tabung.
Tabung mempunyai tiga parameter ukuran yang bisa dihitung yakni keliling, luas dan juga volume.
Sifat – Sifat Tabung

Berikut adalah sifat – sifat tabung, bagian tabung beserta jaring – jaring tabung, antara lain:
- Tersusun atas 3 buah sisi, yakni dua lingkaran sama panjang serta satu buah segiempat.
- 2 lingkaran yang ada pada tabung memiliki peran sebagai tutup tabung dan juga alas tabung.
- Selimut tabung adalah bangun segiempat yang berfungsi untuk mengelilingi tutup serta alas tabung.
- Tabung tidak memiliki titik sudut.
- Tabung memiliki 2 buah rusuk, yakni rusuk yang mengelilingi alas serta tutup tabung.
- Jari – jari tabung merupakan panjang jari – jari lingkaran yang membentuk suatu tabung.
- Tinggi tabung merupakan jarak yang memisahkan antara kedua lingkaran pada tabung.
Rumus Tabung
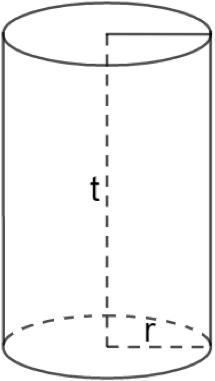
Keterangan:
- t = tinggi
- jari – jari (r) = d÷2
- diameter (d) = 2×r
- π = 22/7 untuk jari – jari dengan kelipatan 7 serta 3,14 untuk jari – jari yang bukan kelipatan 7.
| Nama | Rumus |
|---|---|
| Rumus Volume Tabung (V) | V = π × r × r × t |
| V = π × r² × t | |
| Rumus Luas Permukaan Tabung (L) | L = 2 × π × r × (r + t) |
| Rumus Luas Selimut Tabung (Ls) | Ls = 2 × π × r × t |
| Ls = π × d × t | |
| Rumus Luas Alas Tabung (La) | La = π × r × r |
| Jari – jari (r) diketahui Volume | 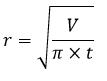 |
| Jari – jari (r) diketahui Luas Selimut | 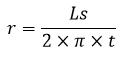 |
| Jari – jari (r) diketahui Luas Permukaan | 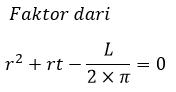 |
| Tinggi (t) diketahui Volume | 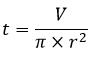 |
| Tinggi (t) diketahui Luas Selimut | 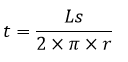 |
| Tinggi (t) diketahui Luas Permukaan | 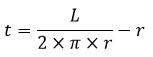 |
Contoh Soal
Berikut adalah contoh soal yang berhubungan dengan tabung, antara lain:
1. Suatu tabung mempunyai diameter 14 cm serta tinggi 10 cm. Hitunglah:
a. Keliling alas tabung?
b. Luas permukaan tabung?
c. Volume tabung?
Jawab:
Diketahui:
Tabung mempunyai diameter 14 cm, sehingga jari – jarinya yaitu 7 cm.
Pembahasan:
a. Keliling Alas Tabung
K= π x d = 22/7 x 14 = 44 cm
b. Luas Permukaan Tabung
Untuk menghitung luas permukaan tabung, maka dibutuhkan luas alas serta luas selimut, jadi:
Luas Alas = π x r2 = 22/7 x 72 = 154 cm²
Luas Selimut = K x t = 44 x 10 = 440 cm²
Sehingga luas permukaan tabung = (2 x Luas Alas) + Luas Selimut = (2 x 154) + 440 =308 + 440 = 748 cm²
c. Volume Tabung
Volume = Luas Alas x t = 154 x 10 = 1540 cm³
2. Berapakah volume suatu tabung yang mempunyai diameter 50 cm dengan tinggi 66 cm?
Jawab:
Diketahui:
Diameter = 50 cm, karena r = 1/2 diameter maka r = 25 cm
Tinggi = 66 cm
Pembahasan:
Volume Tabung = π x r² x t
= (22/7) x 25cm² x 66 cm
= (22/7) x 25 x 25 x 66
= (22/7) x 41250
= 129.642 cm³
3. Seorang tukang kayu sedang memotong sebuah kayu hingga menjadi suatu tabung dengan luas penampang alasanya yaitu 350cm². Tabung / silinder dari kayu itu mempunyai tinggi 45 cm. Hitunglah besar volume tabung atau silinder dari kayu tersebut!
Jawab:
Volume silinder = luas penampang alas atau lingkaran x tinggi
Volume silinder kayu = 350 cm² x 45 cm = 15.750 cm³.
Sehingga volume silinder tersebut yaitu 15.750 cm³.
4. Jika terdapat suatu tabung yang diketahui mempunyai jari – jari sepanjang 16 cm. Hitunglah keliling alas tabung tersebut!
Jawab:
Diketahui:
r = 16 cm
Ditanya:
K = …?
Pembahasan:
K = 2 x π x r
K = 2 x 22/7 x 16
K = 704 / 7
K = 100.57 cm
Sehingga keliling alas tabung tersebut yaitu = 100.57 cm.
5. Hitunglah jari – jari tabung yang memiliki tinggi 8 cm serta volume 2512 cm³!
Jawab:
Diketahui:
t = 8 cm
V = 2512 cm³
Ditanya:
Jari – jari tabung (r) …?
Pembahasan:
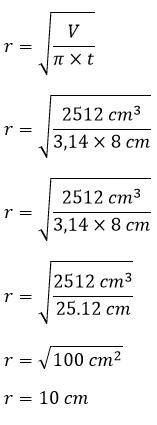
Sehingga jari -jari tabungnya yaitu 10 cm.
6. Hitunglah tinggi tabung yang memiliki jari – jari 10 cm dan volume 2512 cm³!
Jawab:
Diketahui:
r = 10 cm
V = 2512 cm³
Ditanya:
Tinggi tabung (t) …?
Pembahasan:
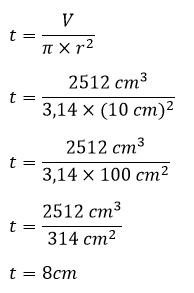
Sehingga tinggi tabung yaitu 8 cm.
7. Hitunglah tinggi tabung yang memiliki jari – jari 5 cm dan luas permukaan 314 cm²!
Jawab:
Diketahui:
r = 5 cm
L = 314 cm²
Ditanya:
Tinggi tabung (t) …?
Pembahasan:
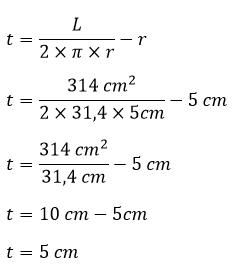
Sehingga tinggi tabung yaitu 5 cm.
8. Hitunglah jari – jari tabung yang memiliki tinggi 21 cm dengan luas permukaan 628 cm²!
Jawab:
Diketahui:
t = 21 cm
L = 628 cm²
Ditanya:
Jari-jari tabung (r) …?
Pembahasan:
Jari – jari tabung memenuhi persamaan sebagai berikut:
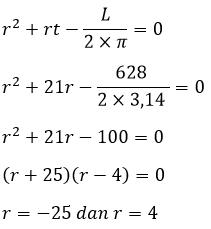
Dari hasil faktor persamaan bisa diuji
r = -25 cm tidak dapat memenuhi syarat, sebab hasil luas permukaan nantinya akan bernilai negatif atau tidak sama dengan 628 cm².
r = 4 cm dapat memenuhi syarat, sebab hasil luas permukaan memiliki nilai 628 cm².
Sehingga jari-jari tabung tersebut yaitu 4 cm.