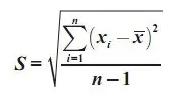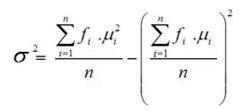Standar deviasi atau varian atau adalah berbagai ukuran keragaman (variasi) data statistik yang paling sering dipakai. Namun ada juga beberapa pengertian dari standar deviasi lainnya seperti di bawah ini.
Daftar Isi
Pengertian Standar Deviasi

Standar deviasi merupakan suatu ukuran yang paling banyak dipakai guna mengukur jumlah sebaran atau variasi dari sejumlah nilai data.
Semakin rendah suatu nilai varian, maka semakin juga mendekati rata – rata, sementara apabila nilai varian semakin tinggi, maka akan semakin lebar rentang variasi datanya.
Sehingga dapat kita tarik kesimpulan bahwa varian adalah besar perbedaan dari suatu nilai sampel pada rata – rata.
Standar deviasi merupakan nilai statistik guna menentukan sebaran data dalam sampel dan seberapa dekat titik data individu pada rata – rata nilai sampel.
Selain itu, varian juga disebut sebagai simpangan baku yang disimbolkan dengan menggunakan alfabet Yunani sigma σ / huruf Latin s.
Di dalam bahasa Inggris, standar deviasi disebut sebagai standard deviation.
Standar deviasi (simpangan baku) adalah akar kuadrat dari varian.
Fungsi Standar Deviasi

Pada umumnya, standard deviation digunakan oleh para ahli statistik maupun orang yang berkecimpung di dunia itu guna mengetahui apakah sampel data yang diambil telah mewakili seluruh populasi.
Namun tak hanya itu saja, ada beberapa fungsi dan manfaat dari standard deviation, seperti:
- Memberikan gambaran terkait persebaran data pada data rata – rata.
- Pada perhitungan fisika bisa memberikan gambaran nilai ketidakpastian ketika sedang mengerjakan pengukuran berulang.
- Memberikan gambaran kualitas data sampel yang didapatkan (apakah dapat mewakili data populasi atau tidak).
- Bisa memberikan gambaran terkait rentang nilai minimal serta maksimal pada data yang didapatkan.
Rumus Standar Deviasi
Berikut adalah empat rumus yang bisa kalian gunakan pada standard deviation, antara lain:
1. Rumus Standar Deviasi Data Tunggal
2. Rumus Standar Deviasi Data Populasi
3. Rumus Standar Deviasi Data Kelompok untuk Sampel
4. Rumus Standar Deviasi Data Kelompok untuk Populasi
Keterangan:
- σ2 : varian atau ragam untuk populasi.
- S2 : varian atau ragam untuk sampel.
- fi : Frekuensi.
- xi : Titik tengah.
- x¯ : Rata – rata (mean) sampel.
- μ : rata – rata populasi.
- n : Jumlah data.
Cara Menghitung Standar Deviasi
Berikut ada tiga cara untuk menghitung standard deviation, antara lain:
1. Menghitung Standar Deviasi Data Tunggal
Tahap 1:
Kalian cari terlebih dahulu nilai rata – ratanya.
X̄ = ΣX : n = 4.4+5.3+5.2+4.8 : 4 = 4.925
Tahap 2:
Kalian cari nilai dari standard deviation tunggalnya.

2. Menghitung Standar Deviasi Data Populasi
Tahap 1:
Kalian cari terlebih dahulu nilai rata – ratanya
X̄= 4.925
Tahap 2:
Kalian cari nilai dari standard deviation populasinya.

3. Menghitung Standar Deviasi di Excel
Rumus yang dapat kalian gunakan untuk menghitung standard deviation di Excel yakni STDEV.
Untuk gambaran singkat perhatikan contoh di bawah ini:
Berdasarkan sampel dari nilai ujian mapel matematika, beberapa siswa di SMA Pelita Rakyat diketahui data sebagai berikut:
80, 60, 80, 90, 70, 80, 95
Hitunglah nilai standard deviation dari data tersebut!
Jawab:
Kalian buka excel kemudian masukkan data ke dalam tabel seperti berikut:

Untuk baris bawah adalah nilai standard deviation. Cara untuk mengetahuinya yakni dengan menekan tombol =STDEV(number1; number 2; dst).
Berdasarkan dari contoh di atas, maka format penulisan rumusnya menjadi:
STDEV(B5:B11)
Nantinya secara otomatis akan keluar hasil standard deviation dari sampel di atas, yaitu 11,70.
Perlu kalian catat bahwa (B5:B11) adalah cell dari data sampel yang kalian masukkan di excel. Sehingga bukan berupa rumus pasti. Sebab data sampel pada contoh di atas ada di cell B5 hingga B11, sehingga kalian masukkan (B5:B11).
Keterangan:
- STDEV mengasumsikan jika argumen merupakan contoh dari populasi. Sehingga data mewakili semua populasi, guna menghitung deviasi standar memakai STDEVP.
- Standard deviation dihitung dengan menggunakan metode “n-1”.
- Argumen bisa berwujud nomor maupun nama, array, referensi yang di dalamnya mengandung angka.
- Nilai – nilai logis serta representasi teks dari nomor yang diketik langsung ke daftar argumen akan dihitung.
- Apabila argumen merupakan suatu array / referensi, maka hanya nomor atau angka pada array / referensi yang akan dihitung. Sel kosong, nilai – nilai logis, teks, dan nilai – nilai kesalahan pada array / referensi akan diabaikan.
- Argumen yang terdapat kesalahan nilai / teks yang tidak dapat diterjemahkan ke dalam nomor / angka akan menimbulkan kesalahan.
- Apabila hendak memasukkan nilai – nilai logis serta representasi teks angka pada referensi sebagai bagian dari perhitungan, maka pakai fungsi STDEVA.
Contoh Soal
Supaya memudahkan kalian dalam mendalami uraian di atas, berikut kami sajikan beberapa contoh soal standar deviasi, antara lain:
1. Soal 1
Data umur berbunga (hari) tanaman padi varietas Pandan Wangi yaitu sebagai berikut: 84 86 89 92 82 86 89 92 80 86 87 90
Berapakah nilai standard deviation dari data tersebut?
Jawab:
| Sampel | y | y2 |
|---|---|---|
| 1 | 84 | 7056 |
| 2 | 86 | 7396 |
| 3 | 89 | 7921 |
| 4 | 92 | 8464 |
| 5 | 82 | 6724 |
| 6 | 86 | 7396 |
| 7 | 89 | 7921 |
| 8 | 92 | 8464 |
| 9 | 80 | 6400 |
| 10 | 86 | 7396 |
| 11 | 87 | 7569 |
| 12 | 90 | 8100 |
| Jumlah | 1043 | 90807 |
Sehingga nilai standard deviation data tersebut adalah:

2. Soal 2
Selepas dikerjakan pengukuran intensitas cahaya sebanyak 10 kali di taman kota, didapatkan data berturut – turut sebagai berikut: 10,2; 10,5;11,0;10,6;12,0;13,0;11,5;12,5;11,3 dan 10,8 W/m2.
Hitunglah standard deviation dari data tersebut!
Jawab:
Pertama kalian tulis datanya di dalam tabel, untuk lebih mudah kalian dapat memakai Microsoft Excel.
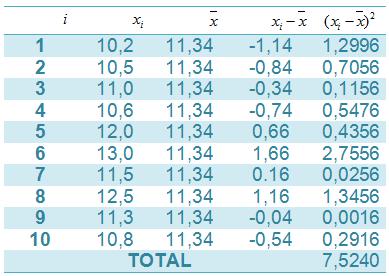
Selepas itu, pakai rumus ragam sampel, sehingga menjadi:

3. Soal 3
Dari hasil survei yang melihat bagaimana kepemimpinan dari 10 orang mahasiswa aktif dalam organisasi intra kampus, diperoleh data yang memperlihatkan nilai kepemimpinan dari 10 responden tersebut yakni:
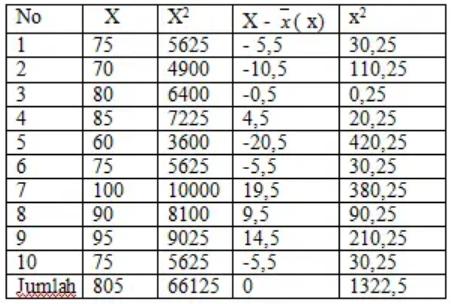
Hitunglah standard deviation dari data tersebut!
Jawab:
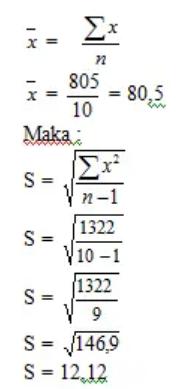
Sehingga bisa kita simpulkan jika rata – rata nilai kepemimpinan mahasiswa yang aktif di dalam organisasi intra kampus tersebut yakni 80, 5 dengan standard deviation (penyimpangan) yaitu 12,12.