Bangun datar yang sangat mudah dikenali bernama lingkaran. Tidak ada titik sudut pada lingkaran, tapi bangun datar tersebut memiliki beberapa unsur, salah satunya adalah tembereng yang terbagi lagi menjadi beberapa jenis.
Unsur lain yang dimiliki lingkaran yaitu tali busur, titik pusat, jari-jari, diameter, busur, juring dan apotema. Pembahasan kali ini akan berfokus pada unsur tembereng dan juring yang meliputi pengertian, rumus serta contoh soalnya.
Daftar Isi
Apa Itu Juring dan Tembereng?
Setiap unsur pada lingkaran memiliki pengertian yang membedakan satu sama lain. Adapun definisi tembereng adalah area di dalam lingkaran yang letaknya diapit oleh 2 unsur lain yaitu busur dan tali busur.
Unsur ini terbagi menjadi 3 jenis yang dibedakan berdasarkan besarnya luas yang dimiliki. Berikut penjelasan dari 3 jenis tersebut:
1. Tembereng Kecil
Disebut dengan tembereng kecil karena unsur lingkaran tersebut mempunyai luas yang terhitung kurang dari luas setengah lingkaran. Busur kecil lingkaran dan tali busur merupakan pembatas area ini.
2. Tembereng Setengah Lingkaran
Selanjutnya, tembereng setengah lingkaran yaitu unsur pada lingkaran yang memiliki luas setara dengan luas setengah lingkaran tersebut.
3. Tembereng Besar
Adapun pengertian tembereng besar adalah unsur lingkaran yang memiliki luas lebih besar dibandingkan jenis yang kecil. Dalam lingkaran, jenis ini merupakan area yang dibatasi oleh busur besar lingkaran dan tali busur.
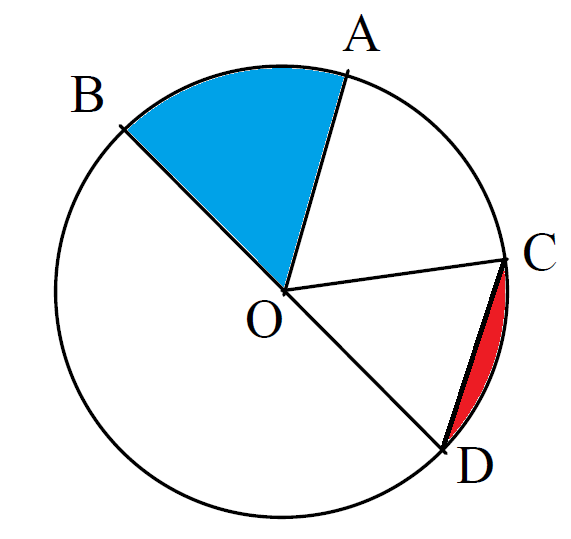
Berikut contoh gambar tembereng dan keseluruhan lingkaran agar lebih mudah untuk mengenali sekaligus membedakan tiap unsurnya:
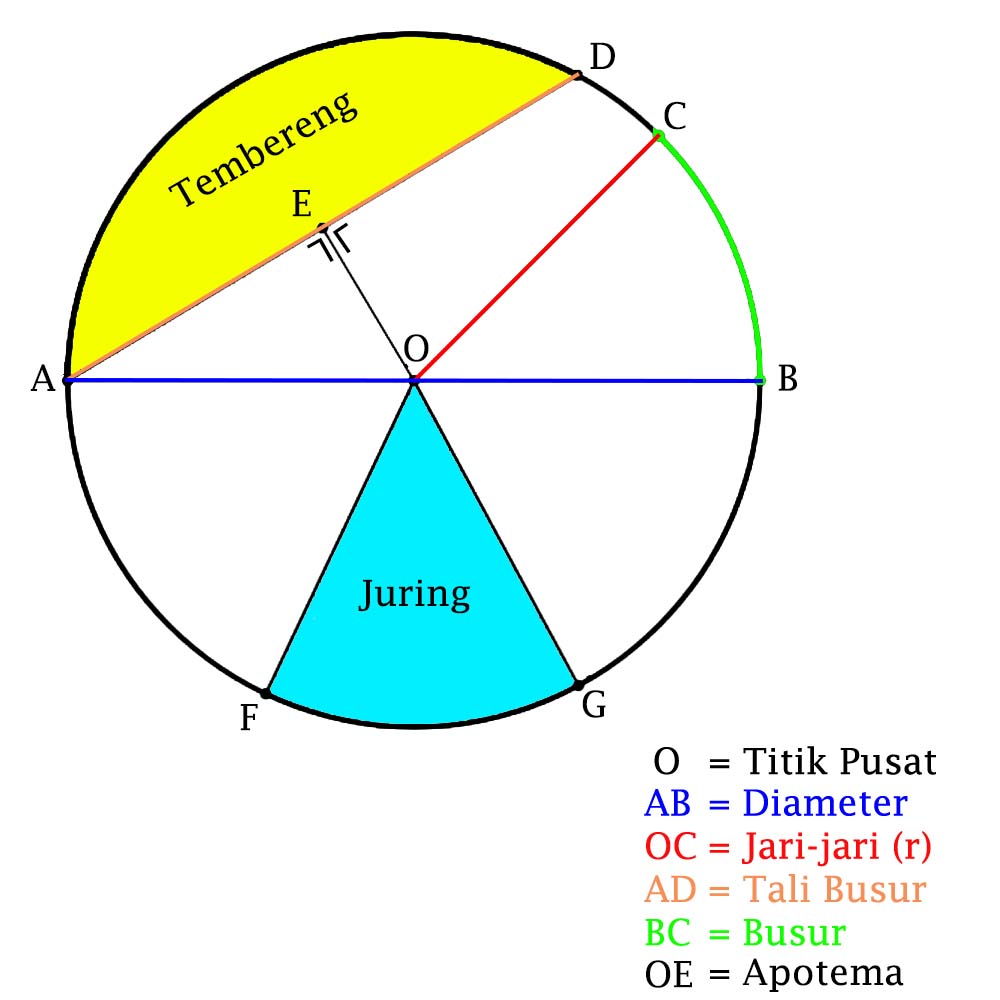
Selanjutnya, apa yang dimaksud dengan juring? Juring adalah salah satu unsur lingkaran yang areanya diapit oleh busur dan jari-jari lingkaran. Area ini dibagi menjadi 2 jenis yakni juring besar dan kecil.
Daerah yang disebut dengan juring kecil ditandai dengan busur kecil lingkaran dan jari-jari yang menjadi pengapit. Sedangkan daerah juring besar diapit oleh busur besar lingkaran beserta jari-jarinya.
Baca: Irisan Dua Lingkaran
Rumus Juring Lingkaran
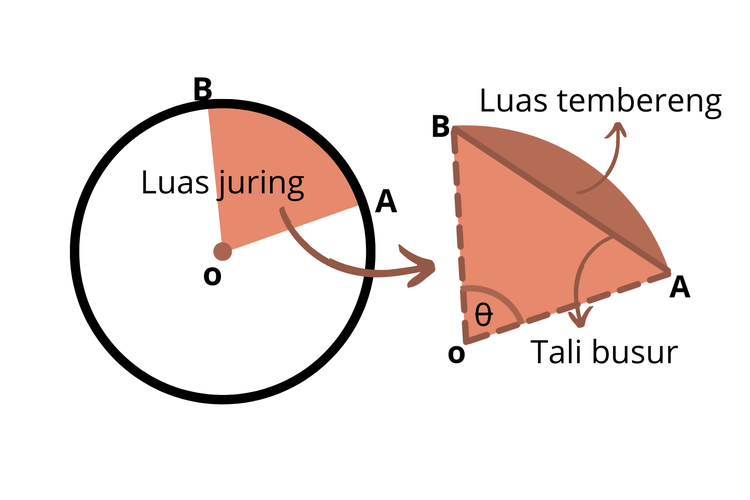
Dalam ilmu matematika, penghitungan luas juring dilakukan dengan cara membagi hasil bagi sudut pusat dengan sudut 3600, setelah itu dikalikan dengan luas lingkaran. Berikut rumus yang digunakan:
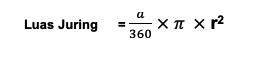
Keterangan rumus:

Pada penerapannya, terdapat permasalahan yang mudah untuk diselesaikan sehingga angka-angka yang diketahui bisa langsung dimasukkan ke dalam rumus. Namun, ada juga jenis soal yang rumit sehingga perlu proses penyelesaian yang lebih panjang sebelum sampai pada rumus tersebut.
Perlu diketahui bahwa luas juring sangat berhubungan dengan penghitungan tembereng. Sebab, hasil dari luas juring digunakan dalam rumus untuk menghitung luas unsur lingkaran tersebut.
Baca: Persamaan Lingkaran
Rumus Tembereng Lingkaran
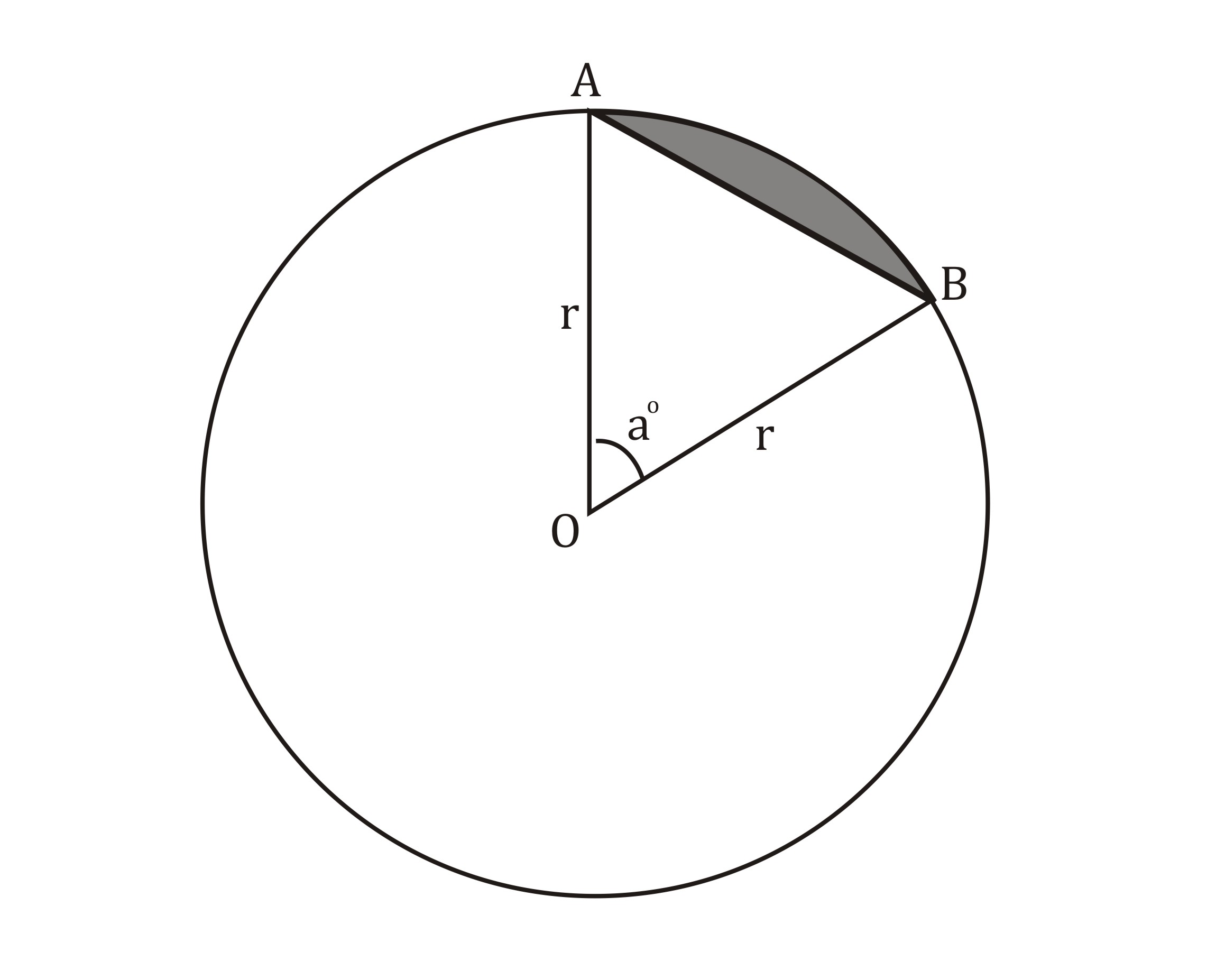
Cara menghitung tembereng yakni dengan mencari selisih yang dimiliki oleh luas segitiga dan luas juring. Maka dari itu, perlu menghitung kedua luas area tersebut agar bisa masuk ke rumus penghitungan luas tembereng.
Adapun rumus yang dipakai yaitu:

Perlu menganalisis soal dengan baik dan melakukan penghitungan dengan cermat karena prosesnya cukup panjang. Walaupun begitu, menghitung tembereng tetap tergolong mudah apabila sudah menemukan angka-angka yang harus dimasukkan ke dalam rumus.
Baca: Diagram Lingkaran
Contoh Soal Juring dan Tembereng
Berikut beberapa contoh soal untuk mengasah kemampuan dalam materi unsur-unsur lingkaran, khususnya juring dan tembereng.
1. Contoh Soal Juring
Berapa luas juring apabila sebuah lingkaran mempunyai jari-jari 10 cm dan sudut pusat juring yang besarnya 600?
Penyelesaiannya:
Dari soal, sudah diketahui bahwa r = 10 cm dan a = 600
Maka, langsung saja angka-angka tersebut dimasukkan ke dalam rumus untuk mengetahui besarnya luas unsur juring:
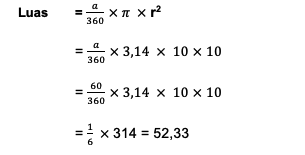
Berdasarkan penghitungan tersebut, maka bisa diketahui bahwa luas juring pada lingkaran sebesar 52,33 cm2.
Sebuah lingkaran memiliki jari-jari 9 cm dengan sudut pusat yang sebesar 900. Cobalah hitung luas juring berdasarkan data tersebut!
Dari soal, diketahui bahwa r = 9 cm dan a = 900, sehingga langsung bisa lanjut ke penggunaan rumus luas juring, yaitu:
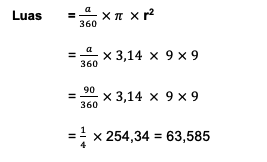
Jadi, sudah jelas bahwa luas yang dimiliki area juring dalam lingkaran tersebut adalah 63,585 cm2.
Lingkaran A memiliki area juring seluas 770 cm2 dan jari-jari 35 cm. Berdasarkan data tersebut, tentukanlah sudut juring!
Diketahui r = 35 cm dan luas juring = 770 cm2. Nilai yang digunakan untuk penghitungan ini yaitu sehingga lebih mudah. Adapun rumus yang dipakai yaitu:

Berdasarkan penghitungan tersebut, maka sudut juringnya sebesar 720
2. Contoh Soal Tembereng
Sebuah lingkaran memiliki jari-jari 21 cm dan sudut juring 600. Maka, berapa luas tembereng yang terdapat dalam bangun datar tersebut?
Sebelum masuk ke rumus inti, perlu mencari luas juring terlebih dahulu dengan rumus sebagai berikut:
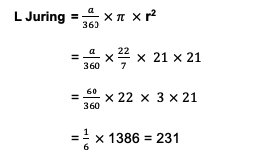
Jadi, luas dari area juring dalam lingkaran sebesar 231 cm2. Setelah itu, saatnya untuk menghitung luas segitiga dengan rumus di bawah ini:
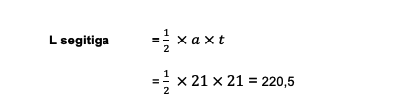
Sekarang, sudah didapatkan luas segitiganya yakni 220,5 cm2
Selanjutnya, masukkan angka-angka tersebut ke dalam rumus inti untuk menghitung luas area tembereng, yakni:
= Luas juring – luas segitiga
= 231- 220,5
10,5 cm2
Dengan begitu, diketahui bahwa area tembereng pada lingkaran tersebut luasnya 10,5 cm2.
Lingkaran A mempunyai tali busur sepanjang 20 cm. Tentukan luas area tembereng pada lingkaran tersebut!
Langkah yang pertama yakni menghitung jari-jari lingkaran. Segitiga yang terbentuk pada lingkaran merupakan segitiga siku-siku sama kaki yang sisi miringnya sepanjang 20 cm dengan sudut 900. Penghitungan jari-jarinya yakni:
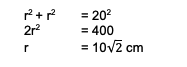
Jadi, jari-jari yang dimiliki oleh lingkaran tersebut sebesar 10 cm atau sama saja dengan 200 cm. Langkah selanjutnya adalah mengetahui luas area juring dan segitiga dalam lingkaran:
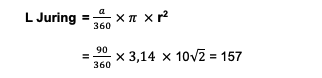
Jadi, area juring dalam lingkaran seluas 157 cm2. Berikutnya, menghitung luas area segitiganya. Sudah dapat diketahui bahwa alas dan tinggi dari segitiga tersebut sama dengan jari-jari lingkarannya yakni 200 cm.
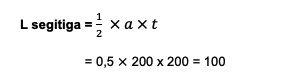
Dengan begitu, area segitiganya memiliki luas 100 cm2
Langkah terakhir adalah menghitung luas area tembereng dengan mencari selisih antara luas area juring dan segitiga.
Luas area juring – luas area segitiga = 157 – 100 = 57 cm2
Akhirnya, bisa diketahui bahwa tembereng dalam lingkaran tersebut seluas 57 cm2
Dua unsur lingkaran yakni tembereng dan juring yang baru saja dibahas, memiliki penghitungan yang terbilang mudah apabila mencermati soal dengan baik. Unsur tersebut juga berhubungan karena luas area juring dipakai untuk menentukan luas area tembereng pada lingkaran.