Transformasi Geometri

Transformasi geometri atau secara bahasa berarti perubahan. Pengertian panjangnya yaitu perubahan pada sebuah bidang geometri yang mencantum posisi, besar dan bentuknya sendiri.

Apabila hasil transformasi kongruen dengan bangunan yang ditranformasikan, maka hal itu disebut sebagai transformasi isometri.

Transformasi isometri sendiri mempunyai dua jenis yaitu transformasi isometri langsung serta transformasi isometri berhadapan.

Transformasi isometri langsung meliputi translasi dan rotasi, sementara untuk transformasi isometri berhadapan termasuk refleksi.

Penasaran apa aja yang termasuk ke dalam materi Transformasi Geometri? Simak selengkapnya berikut ini.

Transformasi Geometri

Transformasi geometri adalah suatu perubahan posisi (perpindahan) dari suatu posisi awal (x , y) menuju ke posisi lain (x’ , y’).

Transformasi geometri terbagi menjadi empat jenis, antara lain:

Jenis-jenis Transformasi Geometri

1.  Translasi (pergeseran)
2. Refleksi (pencerminan)
3. Rotasi (perputaran)
4. Dilatasi (perkalian)

Untuk lebih jelasnya mengenai jenis dari transformasi geometri di atas, yuk simak ulasannya berikut ini.

Jenis-jenis Transformasi Geometri

1. Translasi (Pergeseran)

Translasi adalah salah satu jenis transformasi yang berguna untuk memindahkan suatu titik sepanjang garis lurus dengan arah dan jarak.

Yang berarti, translasi tersebut hanya akan mengalami perpindahan titik ya guys.

Penentuan hasil objek lewat translasi cukup mudah. Caranya hanya dengan cara menambahkan absis serta ordinat dengan jarak tertentu sesuai dengan ketentuan tertentu.

Untuk lebih jelasnya tentang proses translasi bisa dilihat pada gambar di bawah.

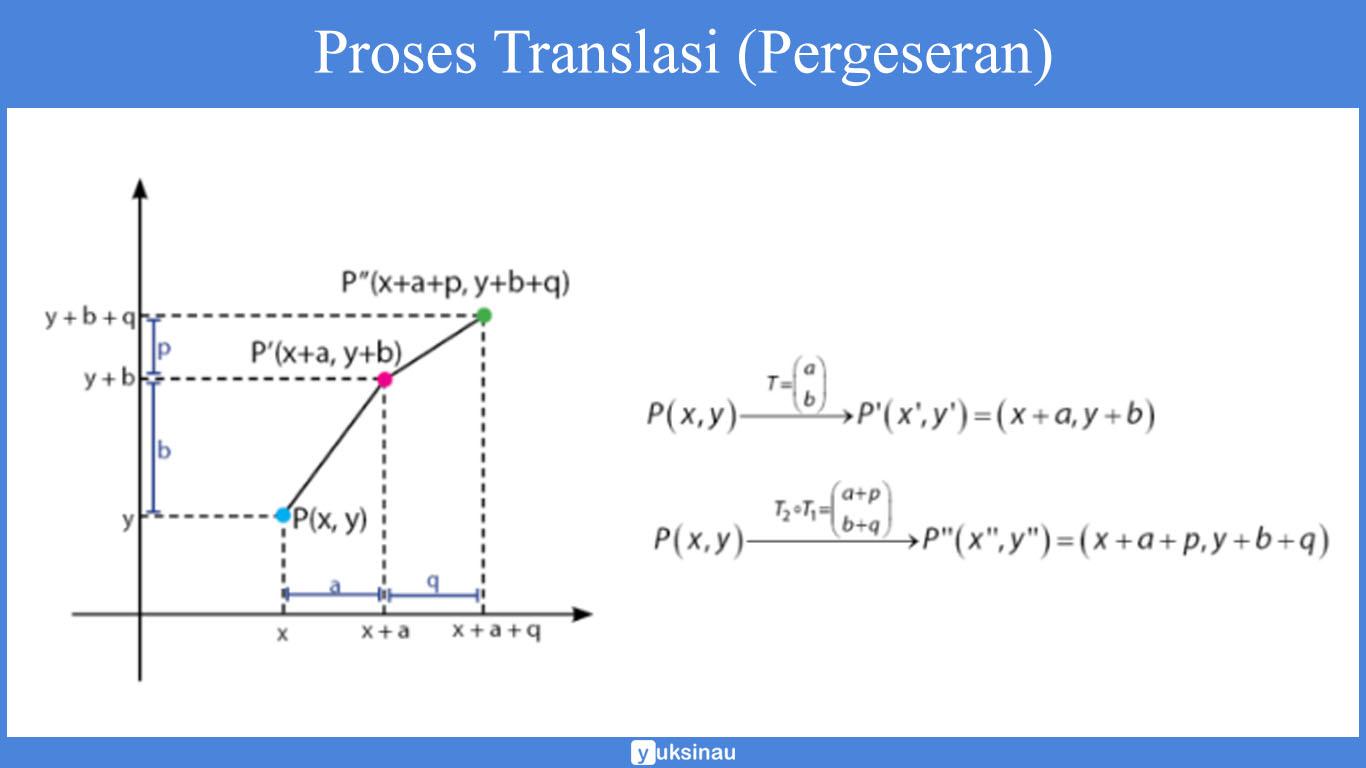
Sebagai contoh:

Jika kalian perhatikan baik-baik, apabila kita sedang naik perosotan, perosotan itu hanya akan mengubah titik awal (puncak perosotan), menuju titik akhir (ujung perosotan).

Berikut adalah gambaran dari translasi:

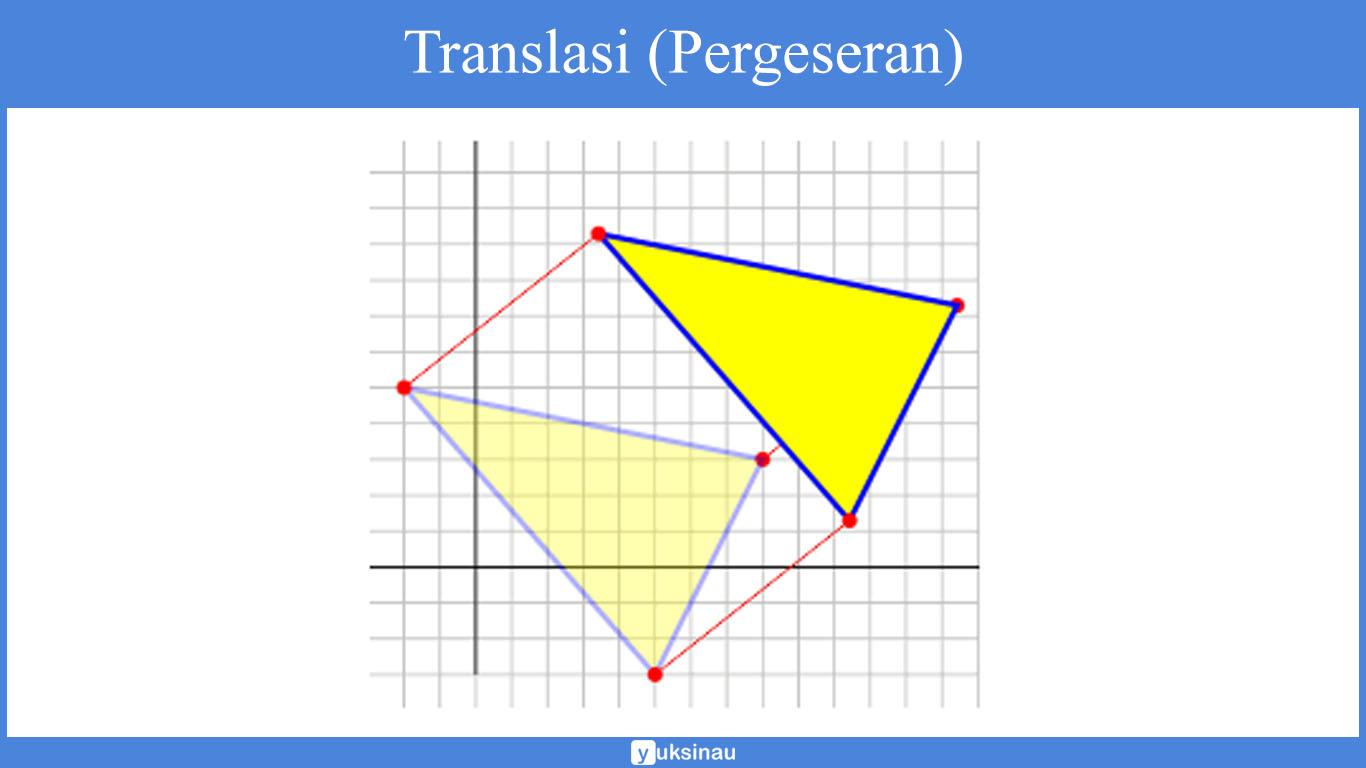
Dari gambar di atas, dapat kita ketahui bahwa translasi hanya dapat berubah posisinya saja. Ukuran akan tetap sama.

Adapun rumus dari translasi, yaitu:

(x’ , y’) = (a , b) + (x , y)

Keterangan:

• (x’ , y’) = titik bayangan
• (a , b) = vektor translasi
• (x , y) = titik asal

2. Refleksi (Pencerminan)

Pembahasan selanjutnya yaitu pencerminan atau yang biasa kita kenal dengan sebutan refleksi.

Sama halnya dengan bayangan benda yang terbentuk pada sebuah cermin. Suatu objek yang mengalami refleksi akan mempunyai bayangan benda yang dihasilkan oleh suatu cermin.

Hasil dari refleksi pada bidang kartesius tergantung sumbu yang menjadi cerminnya.

Refleksi tersebut akan memindahkan seluruh titik dengan memakai sifat pencerminan pada cermin datar.

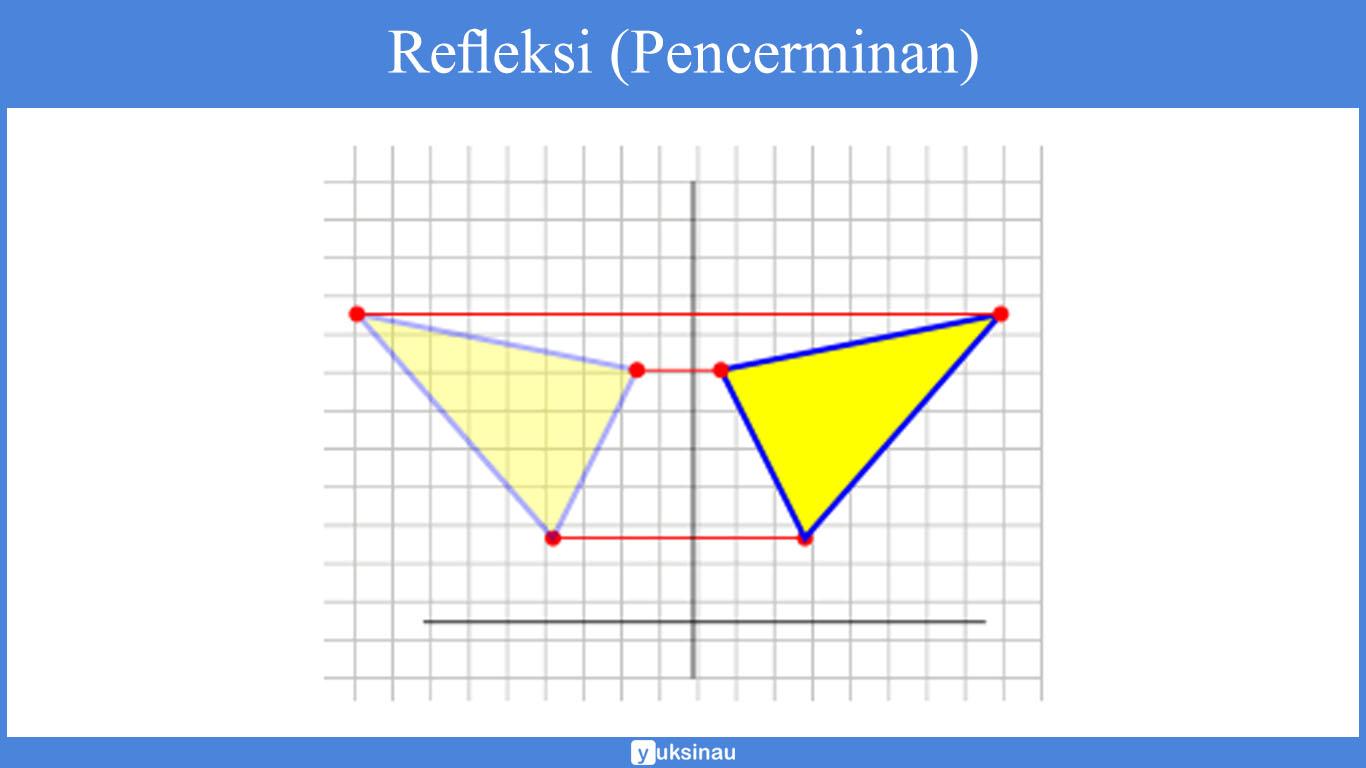
Coba lihatlah garis dan juga beberapa titik merah gambar di atas. Garis dan juga titik-titik merah tersebut berpindah hal itu sama seperti yang ada pada benda yang dihadapkan pada cermin datar.

Sama halnya dengan translasi, refleksi juga mempunyai rumus tersendiri lho. Berikut informasi selengkapnya.

Rumus Umum Refleksi

1. Pencerminan terhadap sumbu -x : (x,y) → (x, -y)
2. Pencerminan terhadap sumbu -y : (x,y) → (-x, y)
3. Pencerminan terhadap garis y = x : (x,y) → (y,x)
4. Pencerminan terhadap garis y = x : (x,y) → (-y, -x)
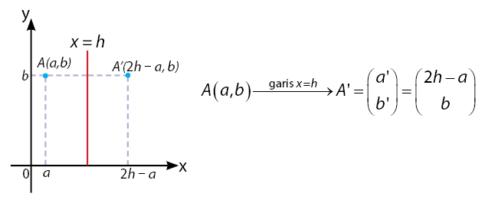
5. Pencerminan terhadap garis x = h : (x,y) → (2h -x,y)
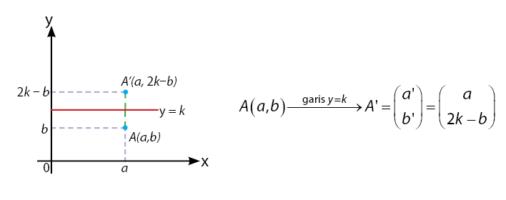
6. Pencerminan terhadap garis y = k : (x,y) → (x, 2k – y)

Selain itu, pembahasan materi refleksi juga memuat tujuh jenis refelksi.

Jenis tersebut diantaranya yaitu: refleksi terhadap sumbu x, sumbu y, garis y = x, garis y = -x, titik O (0,0), garis x = h, dan garis y = k.

Berikut ini adalah ringkasan daftar matriks transformasi yang ada di refleksi atau pencerminan.

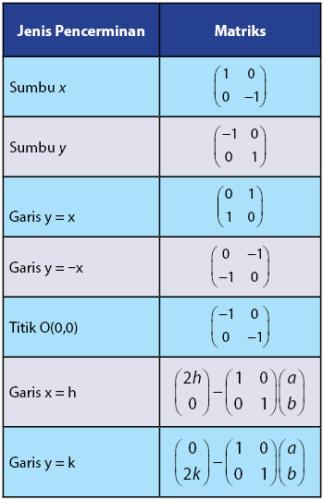
Kemudian, mari perhatikan uraian matriks transformasi untuk masing-masing jenisnya.

Pencerminan terhadap sumbu x

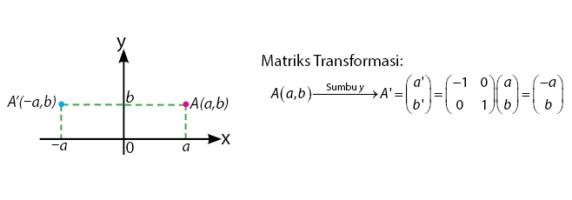
Pencerminan Terhadap Sumbu y

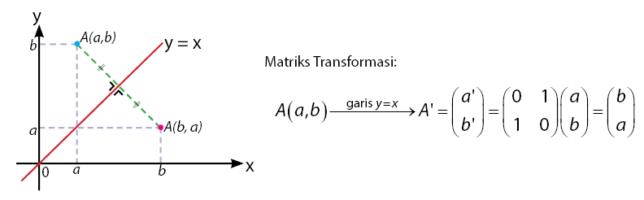
Pencerminan terhadap Garis y = x

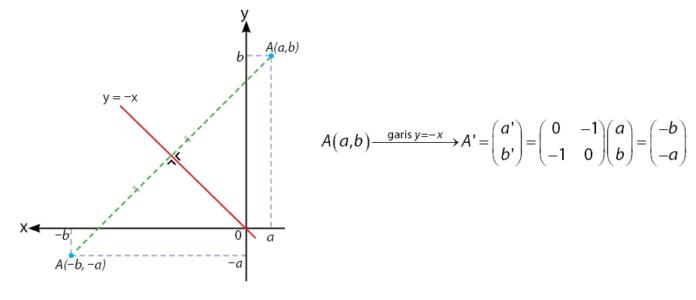
Pencerminan terhadap Garis y = – x 

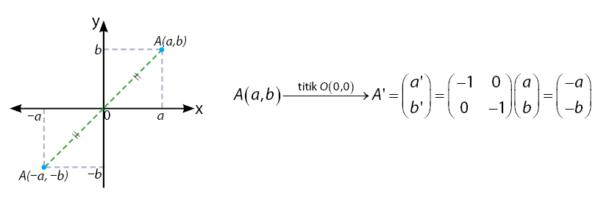
Pencerminan terhadap Titik Asal O(0,0)

Pencerminan terhadap Garis x = h

Pencerminan terhadap Garis y = k

3. Rotasi (Perputaran)

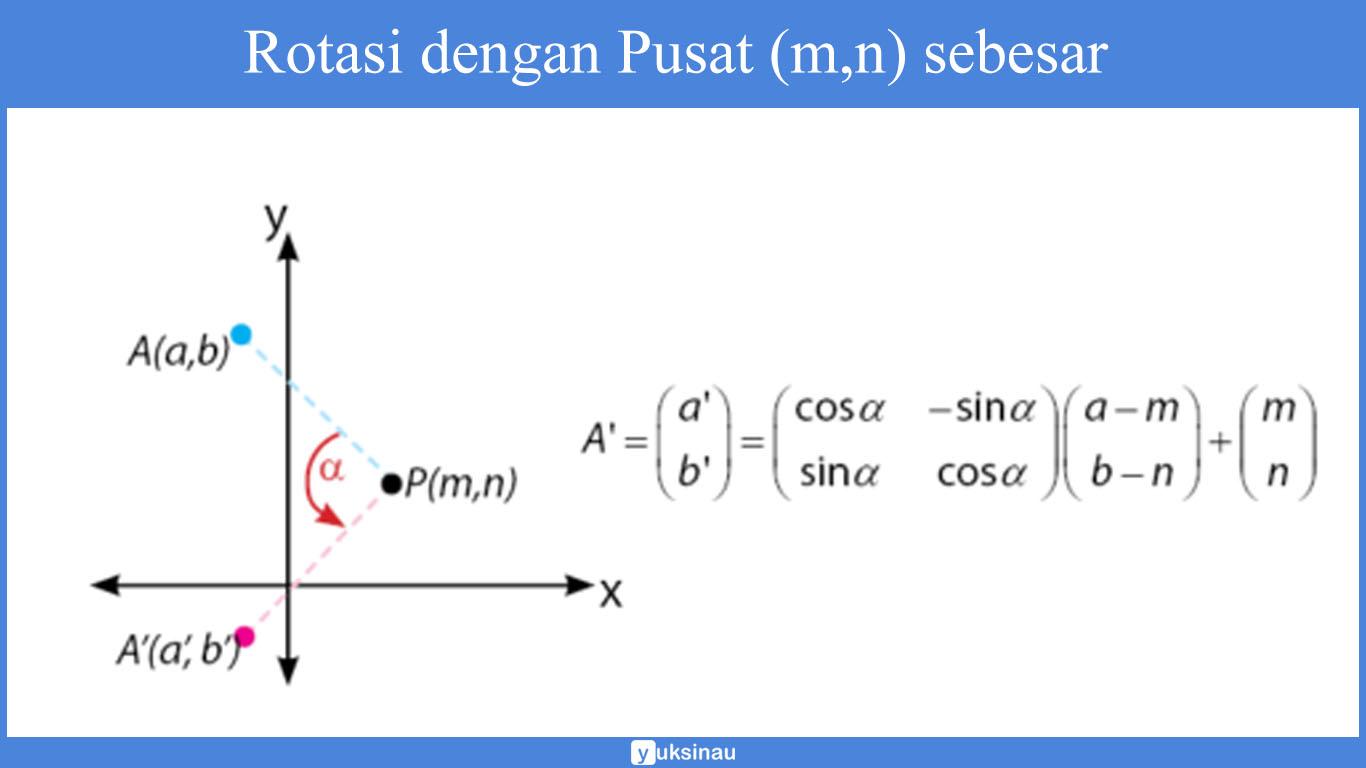
Rotasi atau perputaran adalah sautu perubahan kedudukan atau posisi objek dengan cara diputar lewat suatu pusat dan sudut tertentu.

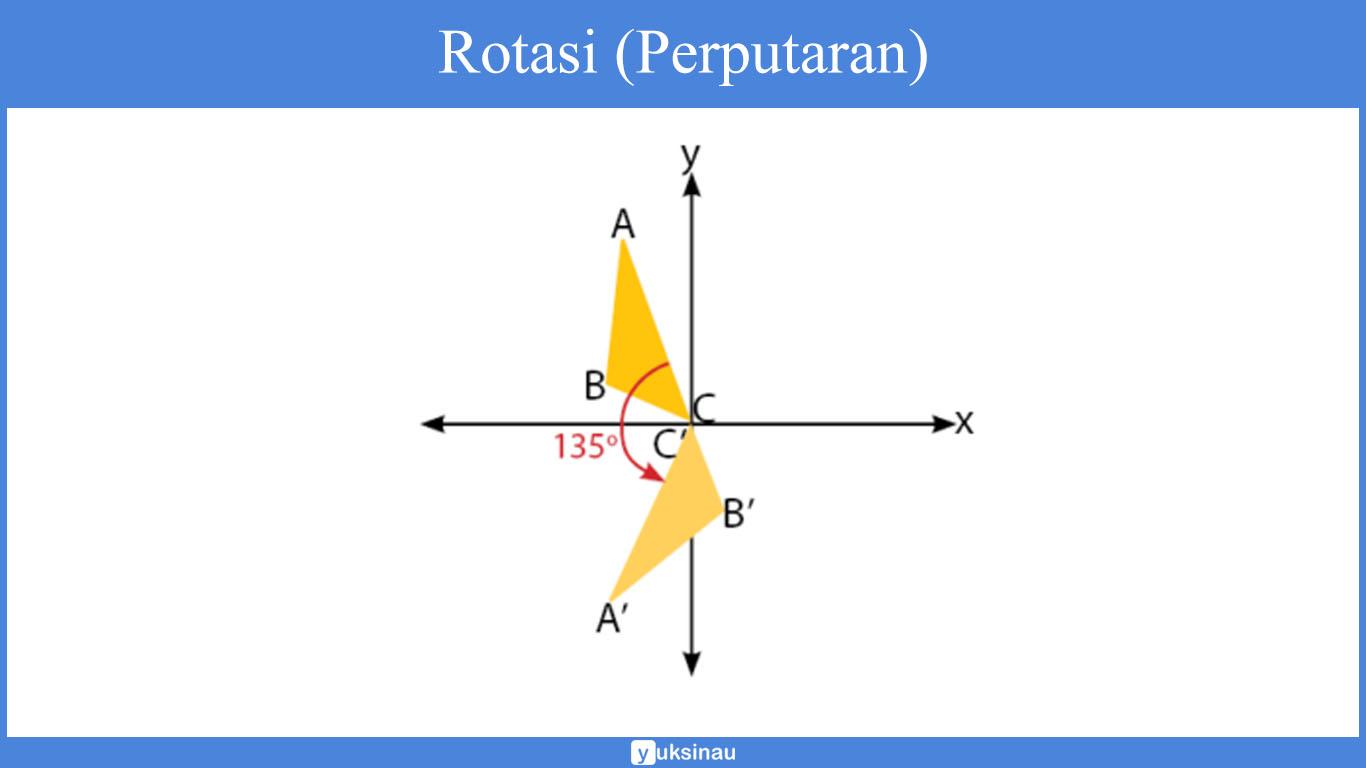
Besarnya rotasi dalam transformasi geometri sebesar α yang telah disepakati untuk arah yang berlawanan dengan arah jalan jarum jam.

Apabila arah perputaran rotasi pada sebuah benda searah dengan jarum jam, maka sudut yang dibentuk yaitu -α.

Hasil dari rotasi sebuah objek tergantung dari pusat serta besar sudut rotasi. Perhatikan perubahan letak kedudukan segitiga yang diputar sebesar 135° dengan pusat o(0,0) pada gambar di bawah ini.

Di kehidupan nyata, bianglala yang sering kita lihat di tempat rekreasi merupakan salah satu contoh dari rotasi dalam transformasi geometri lho. 

Prinsip yang digunakan sama dengan rotasi dalam transformasi geometri, dimana memutar pada sudut serta titik pusat tertentu yang mempunyai jarak sama dengan setiap titik yang diputar.

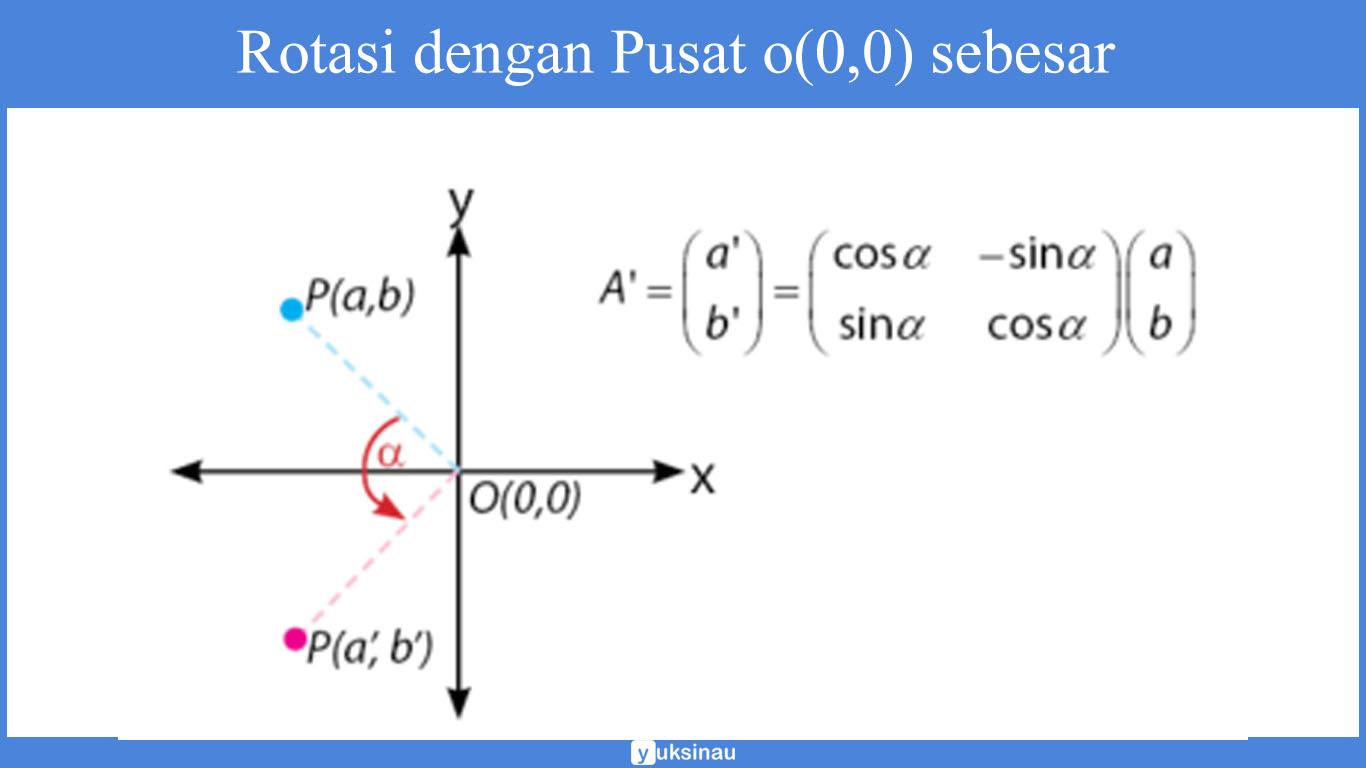
Adapun rumus yang digunakan dalam rotasi transformasi geometri, antara lain:

• Rotasi sebesar 90° dengan pusat (a,b) : (x,y) → (-y + a+b, x -a + b)
• Rotasi sebesar 180° dengan pusat (a,b) : (x,y) → (-x + 2a+b, -y + 2b)
• Rotasi sebesar -90° dengan pusat (a,b) : (x,y) → (y – b + a, -x + a + b)
• Rotasi sebesar 90° dengan pusat (0,0) : (x,y) → (-y, x)
• Rotasi sebesar 180° dengan pusat (0,0) : (x,y) → (-x, -y)
• Rotasi sebesar -90° dengan pusat (0,0) : (x,y) → (y, -x)

Memperoleh hasil rotasi dengan cara menggambarnya terlebih dulu akan sangat tidak efektif.

Maka dari itu kita harus menggunakan metode lain yang bisa digunakan untuk menentukan hasil objek hasil rotasi. Solusinya adalah dengan cara memakai rumus transformasi geometri untuk rotasi.

Simak lebih lanjut rumusnya pada pembahasan di bawah ini.

Rotasi dengan Pusat o(0,0) sebesar α

Rotasi dengan Pusat (m,n) sebesar α

Rotasi dengan pusat (0,0) sebesar α kemudian sebesar β

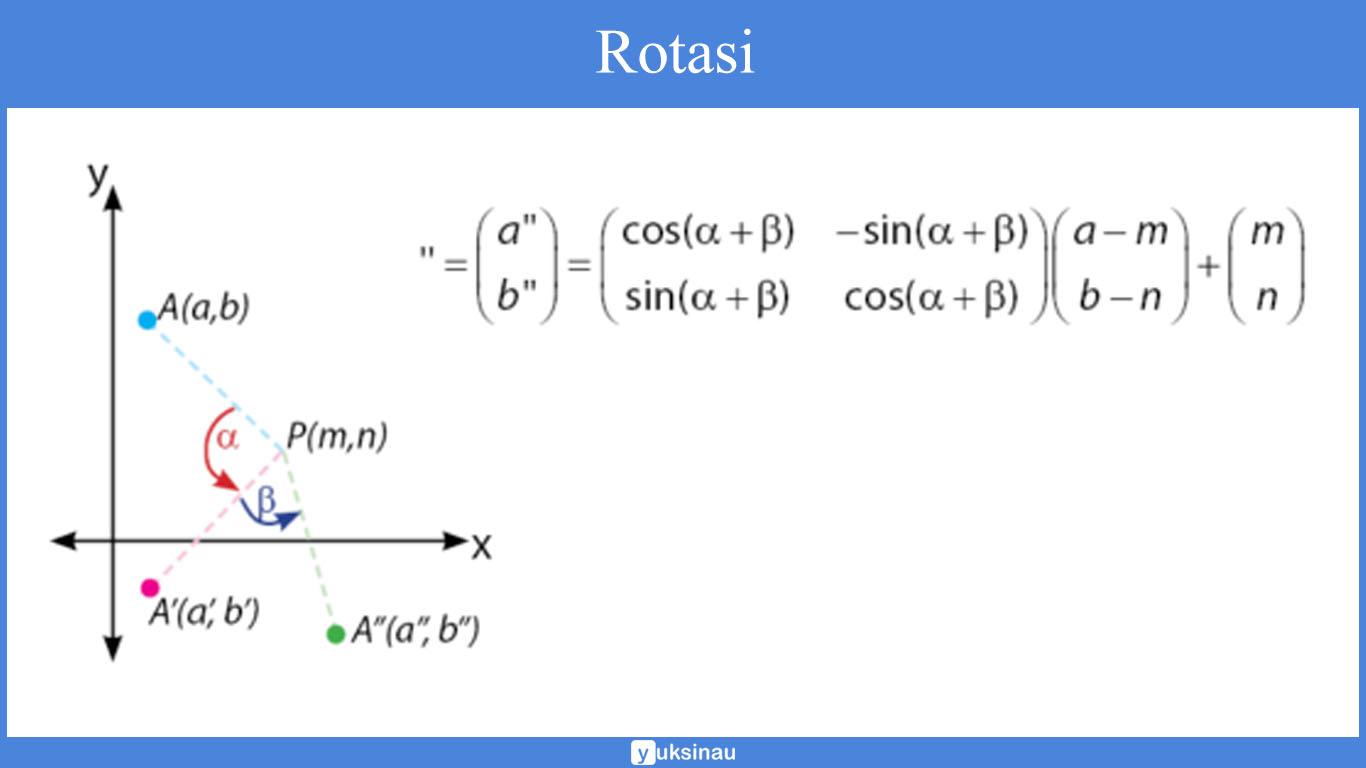
Rotasi dengan pusat P(m,n) sebesar α kemudian sebesar β

4. Dilatasi (Perkalian)

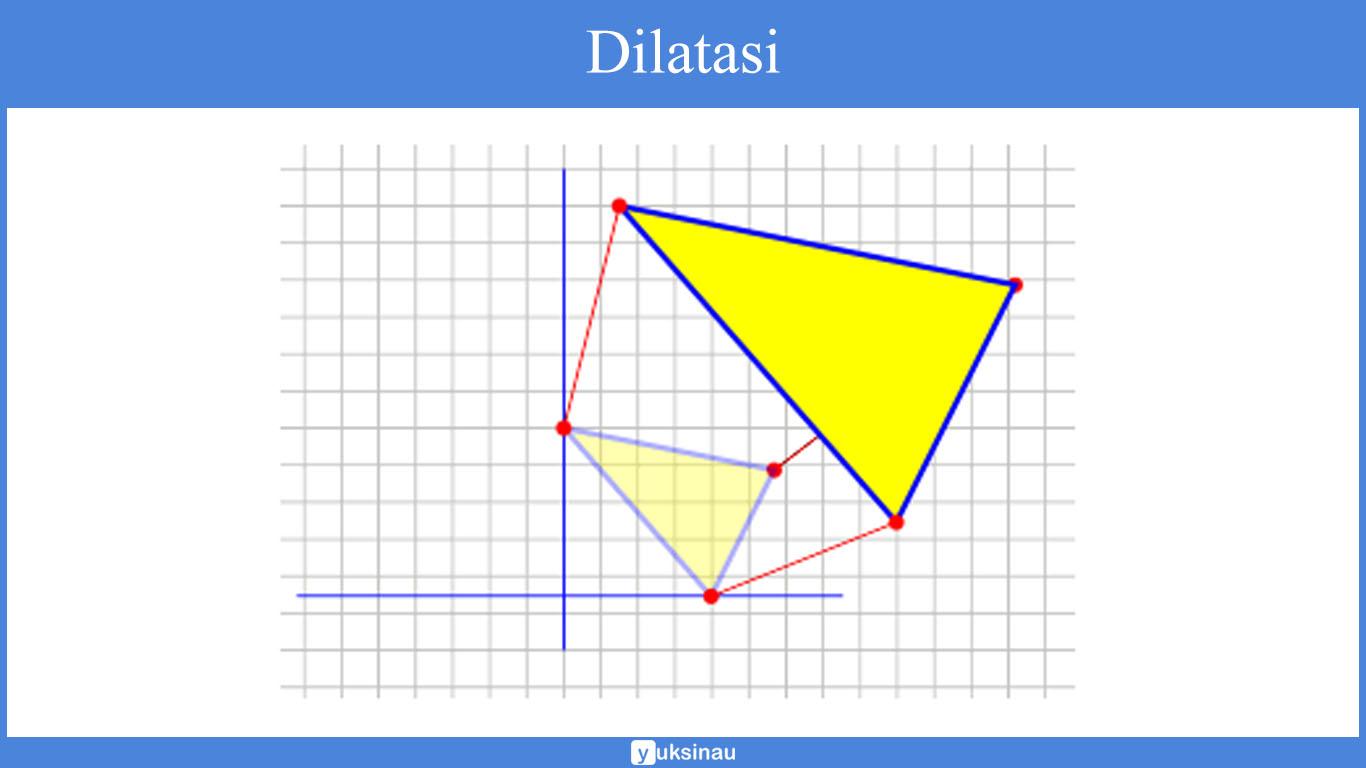
Dilatasi juga dikenal dengan sebagai perbesaran atau pengecilan sebuah objek.

Apabila transformasi pada translasi, refleksi, serta rotasi hanya mengubah posisi benda, maka lain halnya dengan dilatasi yang melakukan transformasi geometri dengan cara merubah ukuran benda.

Ukuran benda bisa akan dibuah oleh dilatasi menjadi lebih besar atau lebih kecil. Perubahan ini bergantung pada skala yang menjadi faktor dari pengalinya.

Dilatasi bisa dipahami sebagai bentuk pembesaran atau pengecilan dari titik-titik yang membentuk sebuah bangun.

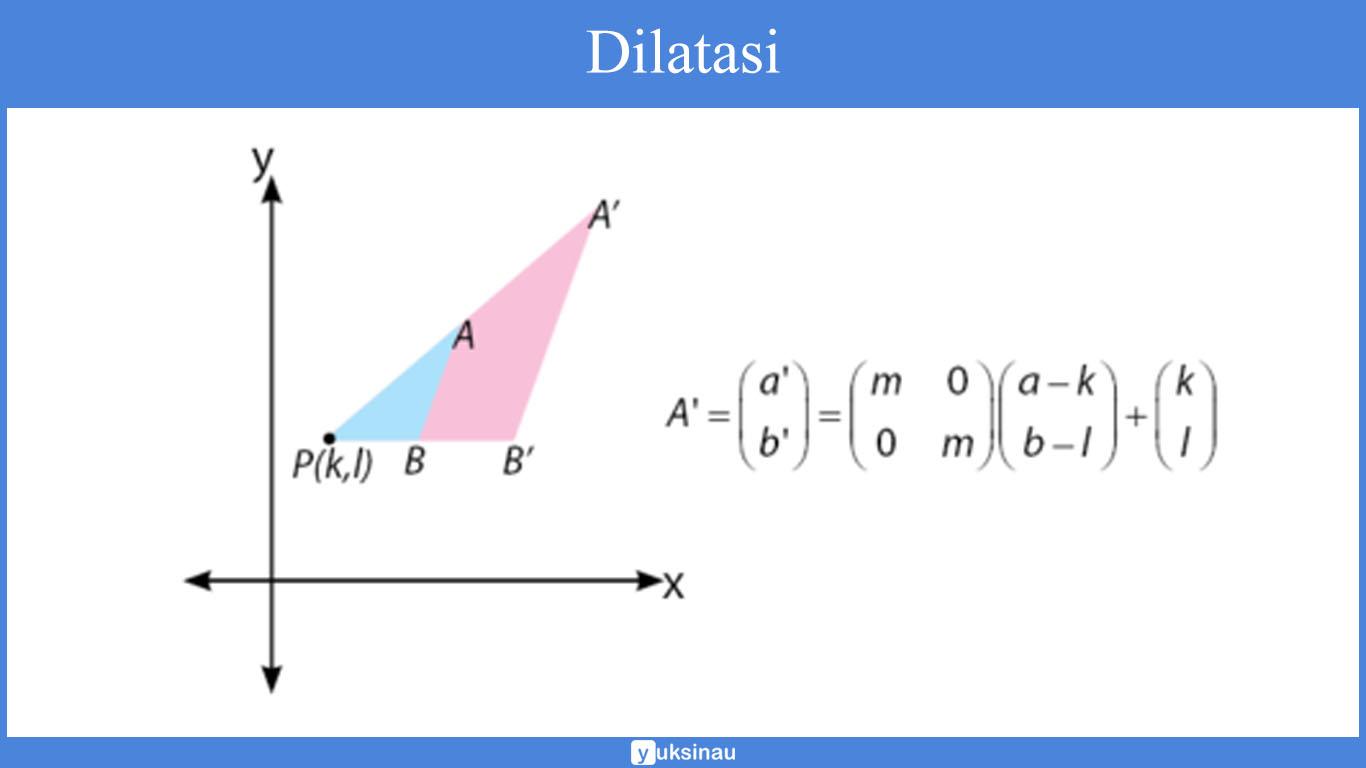
Berikut adalah ilustrasi dari dilatasi:

Rumus pada dilatasi ada dua yang dibedakan menurut pusatnya. Perhatikan uraian rumus untuk transformasi geometri pada dilatasi yang ada di bawah.

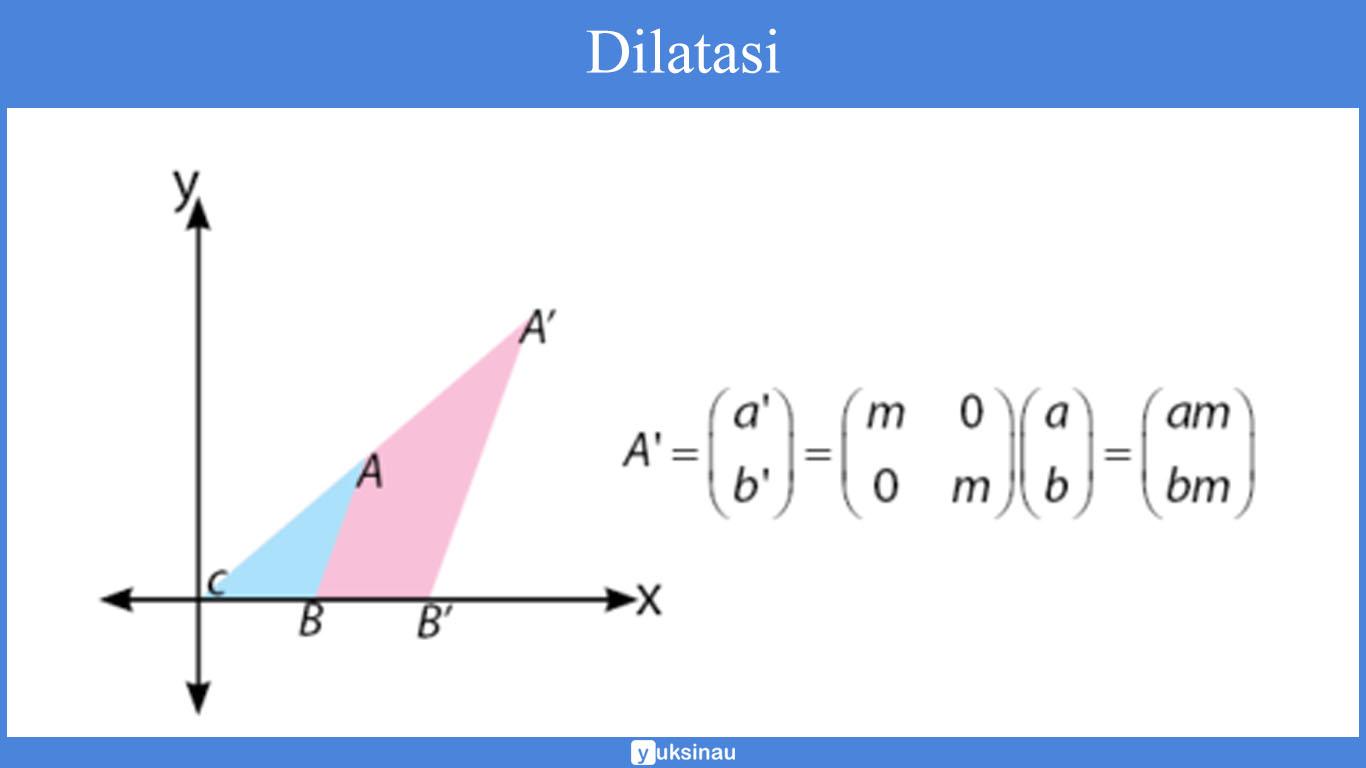
Dilatasi titik A(a, b) pada pusat O(0,0) dengan faktor skala m

Dilatasi titik A9(a,b) terhadap pusat P(k,l) dengan faktor skala m

Demikianlah ulasan singkat mengenai Transformasi Geometri yang dapat kami sampaikan. Semoga ulasan di atas mengenai Transformasi Geometri dapat kalian jadikan sebagai bahan belajar kalian.